跳跃游戏（55）

这道题是让我们从数组的头部看能不能跳到数组的尾部,每次可跳的最大距离也就是目前所在的索引处的值。
思路:

这里我们可以定义1个能跳的最大距离,我们最后只需要拿这个数去和数组的长度去比较，若比数组的最大的长度大的话，就可以跳到最后1个下标,反之则不能。

        //定义能跳的最大距离
        int max_i = 0;

我们需要遍历1边整个数组，拿到每个索引处所对应的值的大小，

特殊情况：在我们的示例二中，最后1个元素的索引为4，但当前能到的最远距离却为3，比最后1个元素的索引值还小，就表示无论怎么跳都跳不到最后1个元素。

 if(max_i < i){
      return false;
  }

其它情况我们只需要算出在当前索引处能到的最大距离，尽量往最远处跳。
如果能够跳的最远距离(max_i) 小于 当前能够跳的最远距离(max_curr),我们就把max_i进行更新,替换成max_curr。

//定义当前能够跳的最大距离
     int max_curr = nums[i] + i;
      if(max_curr > max_i){
          max_i = max_curr; 
       }

最后判断即可

return max_i >= nums.length-1;

代码解答：

class Solution {
    public boolean canJump(int[] nums) {
        //定义能跳的最大距离
        int max_i = 0;
        for(int i = 0;i<nums.length;i++){
            if(max_i < i){
                return false;
            }
            //定义当前能够跳的最大距离
            int max_curr = nums[i] + i;
            if(max_curr > max_i){
               max_i = max_curr; 
            }
        }
        return max_i >= nums.length-1;
    }
}

打家劫舍（198）

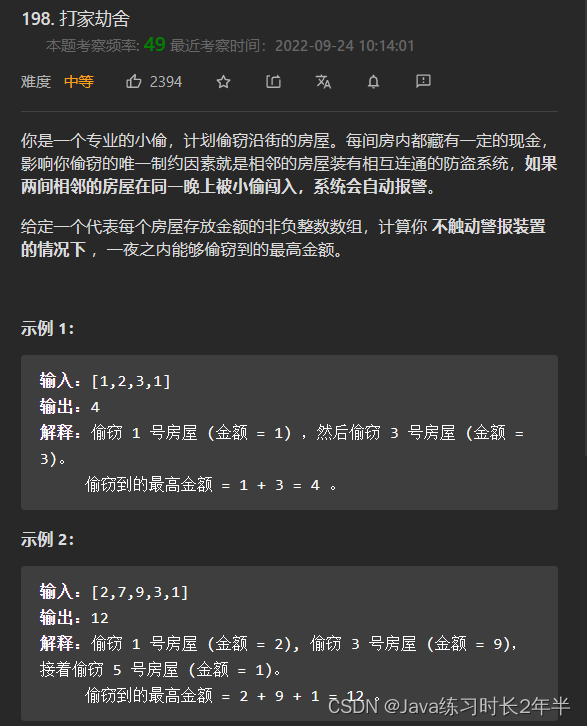
打家劫舍很容易理解就是不能抢2家相互连着的房间，在这种情况下争取抢到的金额最大。这里我们用动态规划来解决
思路:

我们将这个房间抢还是不抢用二维数组[ i ][1],[ i ][0]。1表示抢 0表示不抢

我们创建dp容器

        int n = nums.length;
        int[][] dp = new int[n+1][2];

动态规划的第二步就是给定起始值，因此我们将第一间房间表示出来,
第一间房间我们可以抢或者不抢，
抢：

        dp[0][1] = nums[0];

不抢:

        dp[0][0] = 0;

因此我们就可以用动态方程去完成后面的房间,我们遍历后面的房间同样也是2种情况:

抢(这时前面的房间就不可以抢了因为它们是相邻的):

dp[i][1] = nums[i] + dp[i-1][0];

不抢(这时前面的房间就可以抢或者不抢，我们就需要在这两者种选一个最大值):

dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]);

最后我们只需要返回最后一个房间的前1个房间抢还是不抢的最大值即可

        return Math.max(dp[n-1][1],dp[n-1][0]);

代码解答：

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        int[][] dp = new int[n+1][2];
        dp[0][0] = 0;
        dp[0][1] = nums[0];
        for(int i = 1;i<n;i++){
            //如果不偷
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]);
            dp[i][1] = nums[i] + dp[i-1][0];
        }
        return Math.max(dp[n-1][1],dp[n-1][0]);
    }
}