【模板】KMP字符串匹配

题目描述

给出两个字符串 $s_1$ 和 $s_2$ ，若 $s_1$ 的区间 $[l, r]$ 子串与 $s_2$ 完全相同，则称 $s_2$ 在 $s_1$ 中出现了，其出现位置为 $l$ 。
现在请你求出 $s_2$ 在 $s_1$ 中所有出现的位置。

定义一个字符串 $s$ 的 border 为 $s$ 的一个非 $s$ 本身的子串 $t$ ，满足 $t$ 既是 $s$ 的前缀，又是 $s$ 的后缀。
对于 $s_2$ ，你还需要求出对于其每个前缀 $s^{'}$ 的最长 border $t^{'}$ 的长度。

输入格式

第一行为一个字符串，即为 $s_1$ 。
第二行为一个字符串，即为 $s_2$ 。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 $s_2$ 在 $s_1$ 中出现的位置。
最后一行输出 $s_2|$ 个整数，第 $i$ 个整数表示 $s_2$ 的长度为 $i$ 的前缀的最长 border 长度。

样例 #1

样例输入 #1

ABABABC
ABA

样例输出 #1

1
3
0 0 1

提示

样例 1 解释

。

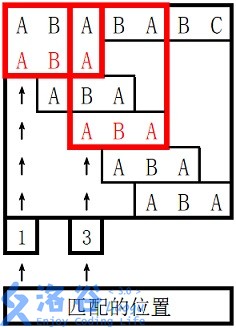对于 $s_2$ 长度为 $3$ 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 $1$ 。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

Subtask 1（30 points）： $|s_1| \leq 15$ ， $|s_2| \leq 5$ 。
Subtask 2（40 points）： $|s_1| \leq 10^4$ ， $|s_2| \leq 10^2$ 。
Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 $\leq |s_1|,|s_2| \leq 10^6$ ， $s_1, s_2$ 中均只含大写英文字母。

分析

KMP算法就是解决字符串匹配问题，然后这个算法最主要的就是next数组的求解；下面介绍下next数组，以及怎么去求；
首先要明白next数组存的是模式串的最长相等前后缀的长度，求next和文本串没有联系；next数组存的是，每个位置的字符他之前的字符串的最长相等前后缀的长度，next[3]=2表示模式串中，索引为[0~3]的字符组成的子串，它的最长相等前后缀长度为2；前缀是一定包含首字母，不包含尾字母的所有子串；后缀是一定包含尾字母，不包含首字母的所有子串；
举个求模式串的next例子：文本串为aabaabaaf，模式串为aabaaf，那么next[0]=0，也就是子串a的最长相等前后缀的长度为0，因为a的前缀、后缀既包含了尾字母，又包含了首字母；next[1]=1，因为子串aa的前缀是a，后缀是a，所以子串aa的最长相等前后缀的长度为1；next[2]=0，因为子串aab的前缀有a、aa，后缀有b、ab，没有相等前后缀，故其值为0；next[3]=1，因为子串aaba的前缀有：a、aa、aab，后缀有a、ba、aba，所以子串aaba的最长相等前后缀的长度为1；next[4]=2，因为子串aabaa的前缀有：a、aa、aab、aaba，后缀有a、aa、baa、abaa，所以子串aabaa的最长相等前后缀的长度为1；next[5]=0，因为子串aabaaf的前缀有：a、aa、aab、aaba、aabaa，后缀有f、af、aaf、baaf、abaaf，所以子串aabaaf的最长相等前后缀的长度为0；
同时上面的分析我们得到了模式串aabaaf的next数组，为：0 1 0 1 2 0 ，那么next有什么用呢？还是上面的例子文本串为aabaabaaf，模式串为aabaaf，可以发现当和文本串匹配到aabaab这里时发现，文本串的b和模式串最后的f不匹配，这时模式串直接回退到 不匹配的字符的前一个字符的next值；也就是回退到模式串索引为4的a字符的next值的位置，此时next[j-1]=2，所以回退到模式串索引为2的位置，也就是b，然后模式串从b开始继续向后匹配（文本串继续从上次中断的位置b继续开始，和模式串进行比对），最后成功匹配；
有的地方可能为了方便不匹配时回退（也就是直接j=next[j]，而不是j=next[j-1]），让前缀表整体右移了，然后第一位默认为-1，也就是-1 0 1 0 1 2，但这里就不后移了；
代码实现——求next：①先初始化i=1,j=0，i为后缀末尾，j为前缀末尾，然后next[0]=0；然后for从i=1开始，遍历模式串，②如果前后缀不匹配，那就让前缀的末尾j回退到不匹配的字符的前一个字符的next值；③如果前、后缀匹配，那就j++④更新当前i的next的值，其值就为j；
代码实现——判断文本串、模式串匹配：遍历文本串，i指向当前遍历到的文本串的位置，j为遍历到的模式串的位置；和求next一样，先初始化i,j，都初始为0，然后判断，如过不匹配（j > 0 && s1[i] != s2[j]），那就让j回退到next[j-1]，匹配的话（s2[i] == s2[j]）j++；然后判断是否已经完全匹配（j == s2.size()），是的话输出首字母在当前文本串所匹配的子串首字母位置；
题意：此题第一问就是判断文本串和模式串是否匹配，如果匹配输出首字母在当前文本串所匹配的子串首字母位置（从1开始计算的，所以输出的时候是+2，i - s2.size() + 1表示模式串首字母所在匹配的文本串的位置，由于从1开始所以多加1，就变成了i - s2.size() + 2 ）；第二问就是输出一下next数组；

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10;

string s1, s2;
int nex[N];//最长相等前后缀的长度

//求模式串s2的next数组
void getNext() {
    //1. 初始化, i为后缀末尾，j为前缀末尾
    int i = 1, j = 0;
    nex[0] = 0;
    for (i = 1; i < s2.size(); ++i) {
        //2. 前后缀不相同,多次回退，所以要用while
        while (j > 0 && s2[i] != s2[j]) {
            //j回退到 next[j-1]
            j = nex[j - 1];
        }
        //3. 前后缀相同
        if (s2[i] == s2[j])
            j++;
        //4. 更新i的next
        nex[i] = j;
    }
}

int main() {
    cin >> s1 >> s2;
    getNext();
    int j = 0;//模式串s2
    for (int i = 0; i < s1.size(); ++i) {//遍历文本串
        //不匹配
        while (j > 0 && s1[i] != s2[j]) {
            //回退到不匹配的那个字符的前一个字符所对应的next值
            j = nex[j - 1];
        }
        //匹配
        if (s1[i] == s2[j])
            j++;
        //说明全部匹配完成
        if (j == s2.size()) {
            cout << i - s2.size() + 2 << endl;
        }
    }
    for (int i = 0; i < s2.size(); ++i) {
        cout << nex[i] << " ";
    }
    return 0;
}