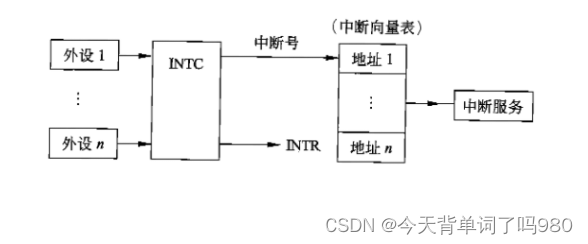
自然数

“自然数的抽象与内在属性：图7中的纯粹五性”

“自然”是数学家对我们所熟悉的1，2，3，4这样的数字所赋予的称呼。自然数是最基本的数学对象，但它们似乎并没有引导我们去抽象地思考。毕竟，单单一个数字5能做些什么呢？它不可能像个棋子一样走来走去。它所具有的似乎是一种内在的属性——某种纯粹的“五性”，当我们观察图7这样的图片时就能立即从中提炼出这样的性质。

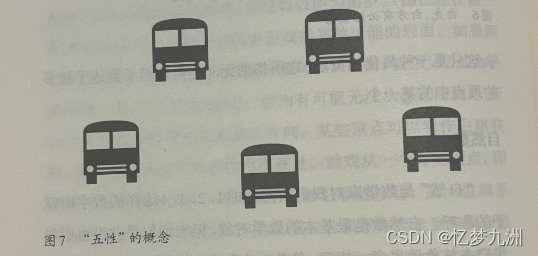
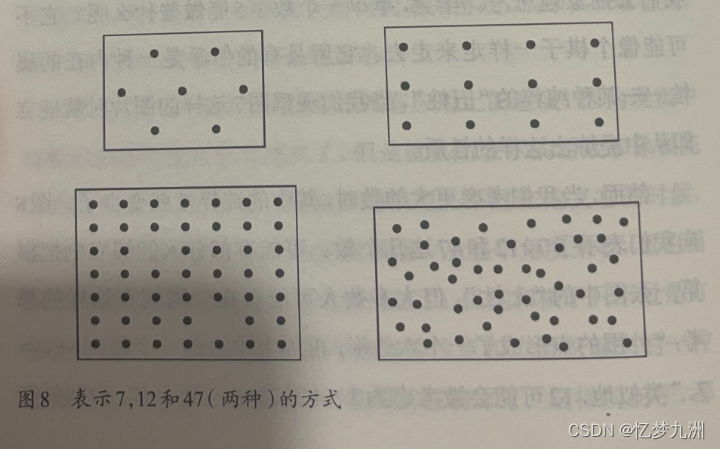
“数的抽象与模式识别：图8中的纯粹性与总数计算”

然而，当我们考虑更大的数时，其中的纯粹性就变少了。图8向我们表示了7，12和47这几个数。可能有部分人能够立刻把握第一张图中的“七性”，但大多数人可能会在一瞬间有这样的思考：“外围的点形成了一个六边形，再加上中心的一个得到6+1=7。”类似地，12可能会被考虑为3X4或2X6。至于47，和别的数字比起来，比方和46相比，一组这个数量的物体就峡乏特别之处。如果这组物体以某种模式排列起来，例如排成少两个点的7X7的阵列，那么我们的知识就可以通过7X7-2=49-2=47迅速地得出总数一共有多少。如若不然，我们就只能去一个个地数，这时我们则是将47视为46之后的那个数，而46又是45之后的那个数，依此类推。

“数字的关联与数系中的作用：超越独立客体的数的理解”

也就是说，当数字变得还不算太大时，我们就已经不再将其视作一些独立的客体了，而开始通过它们的内在属性。它们与其他数字的关联，以及它们在数系中的作用来理解。这也就是我之前说数能“做”什么所要表达的意思。

“数字与算术规则的共同构成：将数字视作计数子的抽象方法”

如我们已经清楚地看到的，数的概念与加法、乘法这样的算术运算紧密相连。比方说，如果没有算术的概念，对1 000 000 017这样的数的意义就只能有很模糊的把握。一个数系并不仅仅是一堆数字，而是由数字及算术规则共同构成的。我们还可以这样来总结这种抽象方法：考虑规则，而不是考虑数字本身。按这种观点，数字就可以被当作某种游戏中的记号（或许应该被称为计数子）。

“推理与分解法：确证38×263=9994的算术过程”

为了对其中的规则有一些了解，让我们来考察一个简单的算术问题：如果我们要确证38×263=9994，应当做什么？多数人可能会用计算器来检查，但要是因故无法这样检查呢？他们可能会作如下的推理。
$$38\times 263=30\times 263+8\times 263$$$$=30\times 200+30\times 60+30\times 3+8\times 200+8\times 60+8\times 3$$$$=6000+1800+90+1600+480+24$$$$=9400+570+24$$$$=9994$$

“推理和定义的应用：为什么相信30×200=6000的推理过程和结果”

为什么上述几步看起来是如此地天经地义呢？比方说，为什么我们会不假思索地相信30× 200=6000？330的定义是3×10，200的定义是2×（10X10），所以我们可以充分相信30X200=（3×10） × （2X（10X10））。但为什么是6000呢？

“乘法的性质和规律：关于乘法的事实和多个数相乘的括号规则”

一般没人会去问这种问题，不过既然有人间了，我们可能会说：
$$(3X10)X(2X(10X10))=(3X2)X(10X10X10)=$$$$6\times 1000=6000$$
我们并没有经过仔细考虑就利用了关于乘法的两个熟知事实：其一，两数相乘时谁先谁后并没有关系；其二，多个数相乘时无论怎样加括号都没有区别。例如，7×8=8X7以及（31×34）×35=31X（34X35）。第二个例子中，中间结果肯定会受到括号位置的影响，但我们知道最终结果是相同的。

“常用的加法和乘法规则：交换律、结合律、单位元和分配律”

这两条规则被称为乘法的交换律和结合律。下面我将列出若干条加法和乘法中常用的规则，也包括上述两条。
A1 加法交换律：对任意两个数a和b，有a+b=b+a。
A2加法结合律：对任意三个数a、b和c，有a+（b+c）=（a+b）+C。
M1乘法交换律：对任意两个数a和b，有ab=ba。
M2乘法结合律：对任意三个数a、b和c，有a(bc）=（ab)c。
M3 1是乘法单位元：对任意数a，有1a=a。
D 分配律：对任意三个数a、b和c，有（a+b)c=ac+bc。

“数学规则在思考中的重要性：理解3x2=6的图像化解析”

我列出这些规则并非试图告诉你这些规则本身多么有意思，而是想请你关注它们在我们的思考中所扮演的角色——即便是在相当简单的数学陈述中。我们对3X2=6的信心大概是基于这样的一种图像：
$$\ast \ast \ast$$$$\ast \ast \ast$$

“运用交换律、结合律和分配律：探索复杂数学问题中的信任与结果”

这样一来，要直接论证38×263=9994就是不可能的了，于是我们要以完全不同的方式来思考这一稍显复杂的事实，其中就要利用到交换律、结合律和分配律。如果的确遵守了这些规则，我们就会相信最后的结果。而且，虽然绝不可能对9994个物体有视觉上的感知，我们也相信结果是正确的。

总结

在数学中，自然数是最基本的数学对象，它们具有一种内在的属性，例如纯粹的"五性"，可以通过对数字的观察进行提炼。然而，随着数字变得更大，纯粹性减少，我们开始关注数字之间的关联和它们在数系中的作用。数字与算术规则紧密相连，数系由数字和算术规则共同构成。推理和定义的应用使我们能够解决复杂的算术问题，例如推导出38×263=9994的过程。乘法的性质和规律，如交换律、结合律和分配律，在解决问题中起到重要的作用。通过运用这些规则，我们可以建立信任并得出正确的结果，即使我们无法直接观察到大量物体的数量。根据上面内容得出结论，数学规则在我们的思考中扮演着重要的角色，帮助我们理解复杂的数学问题和推导数学结论。