前言
Unity中经常会用到向量的运算来计算目标的方位,朝向,角度等相关数据,而这些计算中最常用的就是点乘和叉乘
点乘
一、点乘是什么?
- 定义:a·b=|a|·|b|cos<a,b> 【注:小写字母表示向量,<a,b>表示向量a,b的夹角,取值范围为[0,180]】
- 几何意义:一条边向另一条边的投影乘以另一条边的长度(如图所示)

- 性质1: a*b = |a||b|Cos(θ) ,θ是向量a 和向量 b之间的夹角。
- 性质2: a*b = b*a 满足乘法交换律
- 注意 : 结果不是一个向量,而是一个标量。
二、应用
- 根据点乘计算两个向量的夹角。<a,b>= arccos(a·b / (|a|·|b|))
- 根据点乘的正负值,得到夹角大小范围,点乘>0,则夹角(0,90),点乘<0,则夹角(90,180),可以利用这点判断一个多边形是面向摄像机还是背向摄像机。
- 根据点乘的大小,得到向量的投影长度,反应了向量的长度关系。
- 在生产生活中,点积应用广泛。利用点积可判断一个多边形是否面向摄像机还是背向摄像机。向量的点积与它们夹角的余弦成正比,因此在聚光灯的效果计算中,可以根据点积来得到光照效果,如果点积越大,说明夹角越小,则物理离光照的轴线越近,光照越强。物理中,点积可以用来计算合力和功。若b为单位矢量,则点积即为a在方向b的投影,即给出了力在这个方向上的分解。功即是力和位移的点积。计算机图形学常用来进行方向性判断,如两矢量点积大于0,则它们的方向朝向相近;如果小于0,则方向相反。矢量内积是人工智能领域中的神经网络技术的数学基础之一,此方法还被用于动画渲染(Animation-Rendering)。
三、使用步骤
1.代码示例
代码如下(示例):
/// <summary>
/// 点积
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
private void TestDot(Vector3 a, Vector3 b)
{
// 计算 a、b 点积结果
float result = Vector3.Dot(a, b);
// 通过向量直接获取两个向量的夹角(默认为 角度), 此方法范围 [0 - 180]
float angle = Vector3.Angle(a, b);
// 计算 a、b 单位向量的点积,得到夹角余弦值,|a.normalized|*|b.normalized|=1;
result = Vector3.Dot(a.normalized, b.normalized);
// 通过反余弦函数获取 向量 a、b 夹角(默认为 弧度)
float radians = Mathf.Acos(result);
// 将弧度转换为 角度
angle = radians * Mathf.Rad2Deg;
}
叉乘
一、叉乘是什么?
- 定义:
c = a x b,其中a b c均为向量得到一个与这两个向量都垂直的向量,这个向量的模是以两个向量为边的平行四边形的面积
- 几何意义:
v1和v2向量的叉乘运算:相应元素的乘积的和:v1( x1, y1,z1) x v2(x2, y2, z2) = (y1*z2 - y2*z1)i+(x2*z1 - x1*z2)j+(x1*y2-x2*y1)k;
-
利用三阶行列式计算:
|i j k|
|x1 y1 z1|
|x2 y2 z2|

- 性质1: c⊥a,c⊥b,即向量c与向量a,b所在平面垂直
- 性质2:模长|c| = |a||b| sin<a,b>
- 性质3:(数学上)满足右手法则, a x b = -b x a,所以我们可以使用叉乘的正负值来判断a,b的相对位置,即b是处于a的顺时针还是逆时针方向。
- 注意 :
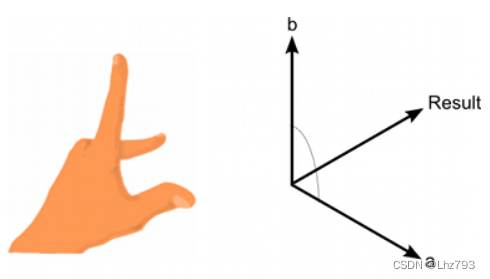
叉乘的右手定则是用来确定叉乘积的方向的。
右手法则:右手的四指方向指向第一个矢量,屈向叉乘矢量的夹角方向(两个矢量夹角方向取小于180°的方向),那么此时大拇指方向就是叉乘所得的叉乘矢量的方向.(大拇指应与食指成九十度)(注意:Unity当中使用左手,因为Unity使用的是左手坐标系)
二、应用
- 1.根据叉乘得到a,b向量的相对位置,和顺时针或逆时针方位。
- 简单的说: 点乘判断角度,叉乘判断方向。形象的说: 当一个敌人在你身后的时候,叉乘可以判断你是往左转还是往右转更好的转向敌人,点乘得到你当前的面朝向的方向和你到敌人的方向的所成的角度大小。
- 2.得到a,b夹角的正弦值,计算向量的夹角(0,90),可以配合点乘和Angle方法计算出含正负的方向。
- 3.根据叉乘大小,得到a,b向量所形成的平行四边形的面积大小,根据面积大小得到向量的相对大小。
三、使用步骤
1.代码示例
代码如下(示例):
/// <summary>
/// 叉乘
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
private void TestCross(Vector3 a, Vector3 b)
{
//计算向量 a、b 的叉积,结果为 向量
Vector3 c = Vector3.Cross(a, b);
// 通过反正弦函数获取向量 a、b 夹角(默认为弧度)
float radians = Mathf.Asin(Vector3.Distance(Vector3.zero, Vector3.Cross(a.normalized, b.normalized)));
float angle = radians * Mathf.Rad2Deg;
// 判断顺时针、逆时针方向,是在 2D 平面内的,所以需指定一个平面,
//下面以X、Z轴组成的平面为例 , (Y 轴为纵轴),
// 在 X、Z 轴平面上,判断 b 在 a 的顺时针或者逆时针方向,
if (c.y > 0)
{
// b 在 a 的顺时针方向
}
else if (c.y == 0)
{
// b 和 a 方向相同(平行)
}
else
{
// b 在 a 的逆时针方向
}
} // 获取两个向量的夹角 Vector3.Angle 只能返回 [0, 180] 的值
// 如真实情况下向量 a 到 b 的夹角(80 度)则 b 到 a 的夹角是(-80)
// 通过 Dot、Cross 结合获取到 a 到 b, b 到 a 的不同夹角
private void GetAngle(Vector3 a, Vector3 b)
{
Vector3 c = Vector3.Cross(a, b);
float angle = Vector3.Angle(a, b);
// b 到 a 的夹角
float sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(a.normalized, b.normalized)));
float signed_angle = angle * sign;
Debug.Log("b -> a :" + signed_angle);
// a 到 b 的夹角
sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(b.normalized, a.normalized)));
signed_angle = angle * sign;
Debug.Log("a -> b :" + signed_angle);
}总结
点乘可以判断出目标物体在我的前方还是后方。大于零在前方,小于零在后方。
叉乘可以判断出目标物体在我的左边还是右边。大于零在右方,小于零在左方。