F-Redundant Paths_2022图论班第二章连通性例题与习题 (nowcoder.com)

 

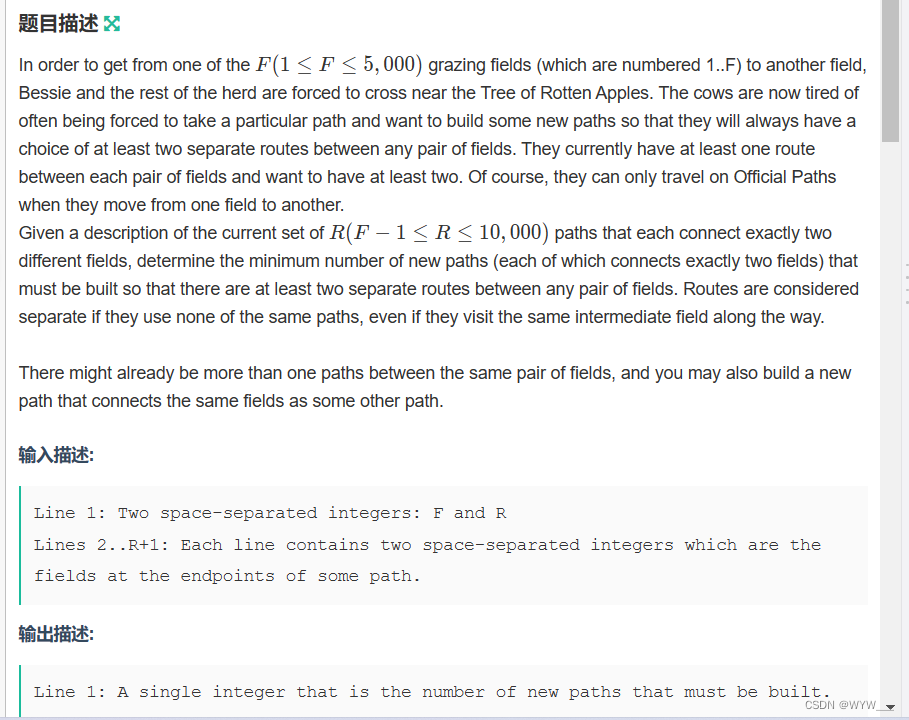
为了从F(1 \leq F \leq 5000)F(1≤F≤5000)一块牧场(编号为1..F)到另一块牧场，贝西和牛群的其他成员不得不穿过烂苹果树附近。奶牛现在厌倦了经常被迫走一条特定的路，想要建造一些新的路，这样它们就总是可以在任何一对田地之间选择至少两条不同的路。他们目前在每个字段对之间至少有一条路由，并且希望至少有两条。当然，当他们从一个领域转移到另一个领域时，他们只能走官方路线。

给定当前连接两个不同字段的R(F -1 \leq R \leq 10,000)R(F -1≤R≤10,000)路径集合的描述，确定必须建立的最小数量的新路径(每条路径正好连接两个字段)，以便在任意一对字段之间至少有两条独立的路由。如果路由没有使用相同的路径，那么它们被认为是分离的，即使它们访问了相同的中间字段。

同一个字段对之间可能已经有多条路径了，你也可以构建一条新的路径来连接相同的字段。

输入描述:

第1行:两个用空格分隔的整数:F和R

行2 . .R+1:每一行包含两个空格分隔的整数，它们是某个路径端点的字段。

输出描述:

第1行:一个整数，表示必须构建的新路径的数量。

示例1

输入

复制

7 7

1 2

2 3

3 4

2 5

4 5

5 6

5 7

输出

复制

2

说明

示例说明:

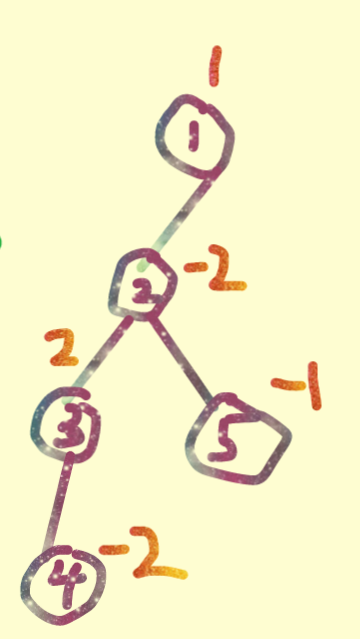
路径的可视化如下:

从1到6和从4到7构建新的路径满足了这些条件。

检查一些路由:

1 - 2: 1 - > 2和1 - > 6 - > 5 - > 2

1 - 4: 1 - > 2 - > 3 - > 4和1 - > 6 - > 5 - > 4

3 - 7: 3 - > 4 - > 7和3 - > 2 - > 5 - > 7

实际上，每一对字段都由两条路由连接。

添加其他路径也可能解决这个问题(比如从6到7添加一条路径)。然而，添加两条路径是最小值。

题解:

一个点到另一个点必须经过一条边,说明存在割边,我们现在要解决,如何加最少的边,使其不存在割边

在一个边联通分量内,是不存在割边的(不需要考虑),所以我们可以把边联通分量缩成点

最后图应该是一棵树,经过观察我们可以发现,只要把数上所有入度为0的点相互连接即可

答案就是(入读为一的点+1)/2

#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<map>
#include<cstring>
#include<cmath>
#include<stack>
#include<set>
using namespace std;
#define int long long
typedef pair<int,int> PII;
const int N = 200;
vector<int> p[N];
int dfn[N];
int vis[N];
int low[N];
int siz[N];
int color[N];
int idx,cnt;
stack<int> s;
int rd[N];
void tarjin(int u,int fa)
{
	dfn[u] = low[u] = ++idx;
	vis[u] = 1;
	s.push(u);
	for(auto v:p[u])
	{
		if(v == fa)
		continue;
		if(!dfn[v])
		{
			
			tarjin(v,u);
			low[u] = min(low[u],low[v]);
		}
		else if(vis[v])
		{
			low[u] = min(low[u],dfn[v]);
		}
	}
	if(dfn[u] == low[u])
	{
		++cnt;
		while(1)
		{
			int t = s.top();
			s.pop();
			color[t] = cnt;
			siz[cnt]++;
			vis[t] = 0;
			if(t == u)
			break;
		}
	}
}
int a[200050],b[200050];
map<int,int>f[20050];
void solve()
{
	int n,m;
	cin >> n >> m;
	
	for(int i = 1;i <= m;i++)
	{
		int x,y;
		cin >> x >> y;
		a[i] = x;
		b[i] = y;
		p[x].push_back(y);
		p[y].push_back(x);
	}
	for(int i = 1;i <= n;i++)
	{
		if(!dfn[i])
		tarjin(i,0);
	}
	for(int i = 1;i <= m;i++)
	{
		int u = color[a[i]],v = color[b[i]];
		if(u!=v)
		{
			if(f[a[i]][b[i]])
			{
				continue;
			}
			f[a[i]][b[i]] = f[b[i]][a[i]] = 1;
			rd[u]++;
			rd[v]++;
		}
	}
	if(cnt == 1)
	{
		cout<<0;
	}
	else
	{
		int sum = 0;
		for(int i = 1;i <= cnt;i++)
		{
			sum += (rd[i] == 1);
		}
		cout << (sum + 1)/2;
	}
}
//1 -7 1 -7
signed main(){
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int t = 1;
//	cin >> t;
    while(t--)
	{

		solve();
	} 
}
//3 3 2 2 1 0
//1 2 1 1 1 0