一,题目

Description

在草原上有N个部落，每个部落都有其坐标(xi,yi)

每个部落都有个武力值，可正可负

由于部落间只能通过马匹来传递信息

于是只有当两个部落间的距离为1的时候，两个部落才有可能进行联系，距离计算公式为

abs(xi-xj)+abs(yi-yj)

现在希望从N个部落中选出一些部落来，满足下面两个条件

1:它们是连通的

2:它们的武力值加起来最大化

Format

Input

第1行是一个整数N（2 <= N <= 1000），表示部落的个数

以下N行中，第i行(1 <= i <= N)有三个整数，Xi, Yi, Ci依次表示第i部落的坐标与武力值

-10^6 <= Xi, Yi <= 10^6，-100 <= Ci <= 100。

Output

如题

Samples

输入数据 1

5

0 0 -2

0 1 1

1 0 1

0 -1 1

-1 0 1

输出数据 1

2

Hint

将给出的5个点全部选中

---

二，思路

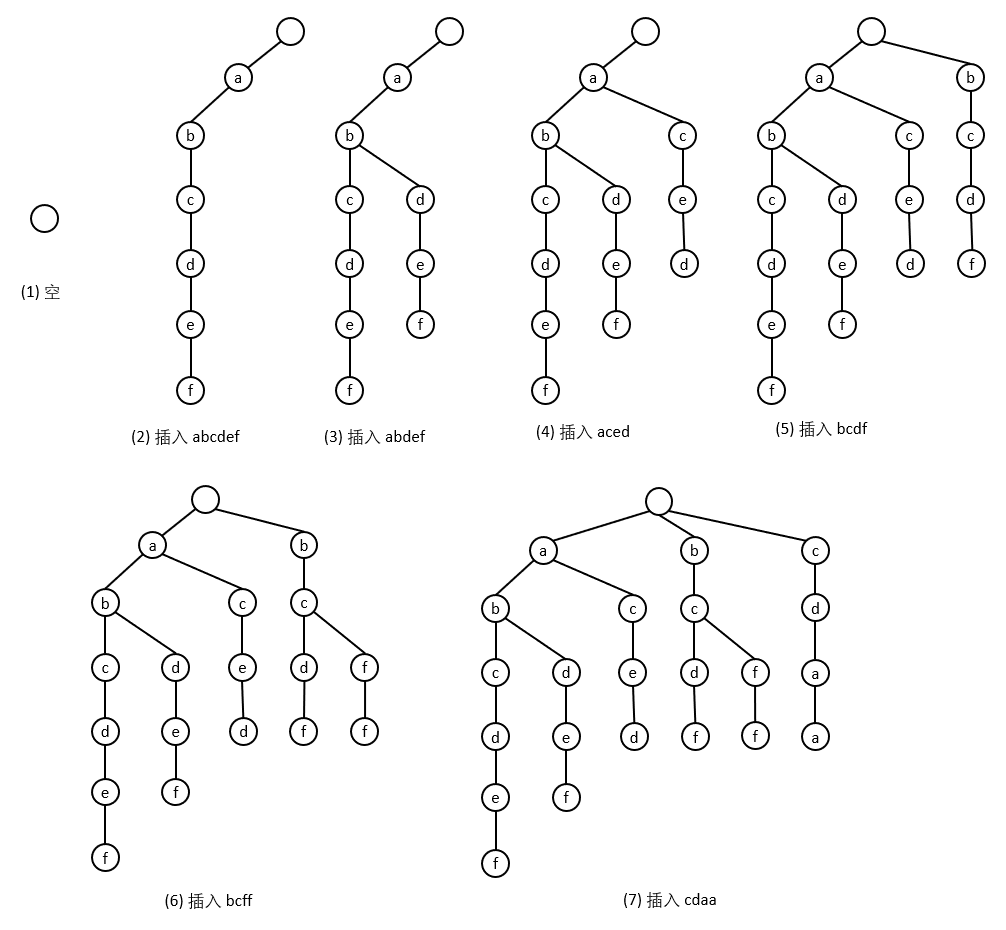
我们来模拟一下我自己造的一个样例（横向为x,竖向为y,方框内的数字为(x,y)的武力值,圈起来的数字为节点编号）:

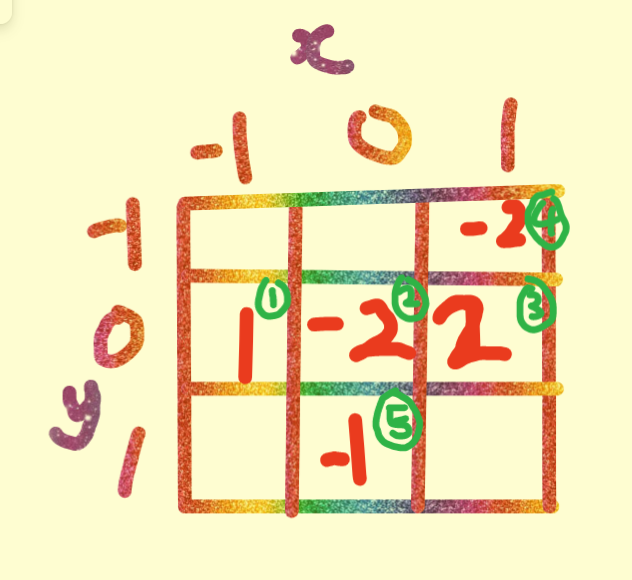
step 1.连树的边

因为在这里只有当两个部落间的距离为1的时候，两个部落才有可能进行联系,所以联系可以看成将2个节点进行连边。那么具体做法就是暴力枚举i和j,判断第i个节点离第j个节点的距离是否等于1,等于1则对i,j进行连一条边权为1的边。

具体代码:

//(bll[i]就是输入第i个节点的各个信息,bll[i].x就是第i个节点的x坐标,y同理。)
for(int i = 1;i <= n;i++)
    for(int j = i + 1;j <= n;j++)
      if(abs(bll[i].x - bll[j].x) + abs(bll[i].y - bll[j].y) == 1)//如果i->j的距离为1
      {
        adeg(i,j,1); //双向建边
        adeg(j,i,1);
      }

那么根据上述思路对前面造的样例进行操作的树如下（彩虹色标记的是第i个节点的武力值）:

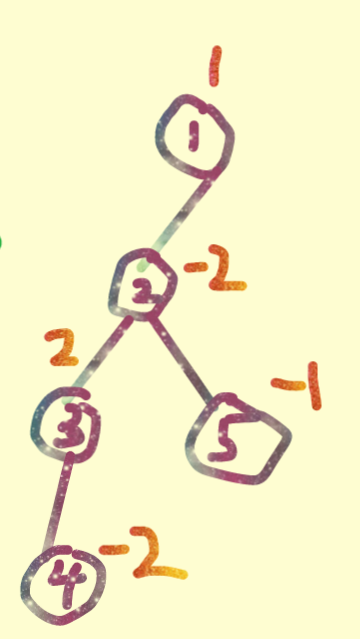
然后就要进行一波玄学般的dfs操作了。

step 2.dfs

首先我们在结构体中再加一个变量z储存以i为根的子树中选出满足题目要求的一些部落的武力值之和。

dfs的过程:首先将bll[beg].z初始化成他本身的武力值(因为在以beg为根的这棵子树中自己一定会被选)，然后将beg的vis标记成1表示已经遍历过beg了。然后遍历beg的子节点，并去重(自己已经经过了的点不需要再遍历)，然后判断如果此时正在遍历的子节点的z的值是正数就接受该子树所选部落的最大武力值之和,将 bll[beg].z += bll[v].z，即可。

void dfs(int beg,int fa)
{
  bll[beg].z = bll[beg].wl;//bll[beg].z初始化成他本身的武力值(因为在这棵子树中自己一定会被选)
  vis[beg] = 1;
  for(int i = now[beg]; i; i = pre[i])
  {
      int v = son[i];
      if(v == fa || vis[v]) continue;//去重
      dfs(v,beg);//递归
      if(bll[v].z > 0) bll[beg].z += bll[v].z;
//判断如果此时正在遍历的子节点的z的值是正数就接受该子树所选部落的最大武力值之和,将 bll[beg].z += bll[v].z
  }
}

step 3.输出答案

最后的答案其实就是这n个节点的z的最大值。

for(int i = 1;i <= n;i++) maxn = max(maxn,bll[i].z);
  cout<<maxn;

---

三，整体代码

#include<bits/stdc++.h>
using namespace std;
#define int long long 
/*
pre[j]:对于第i条边来说，它的上一条边是哪一条边
now[x]:对于点x来说，最后一条描述它充当父结点的边是哪一条边
son[i]:在第i条边中，充当子结点的点是哪一个
*/
int eg,pre[100001],now[100001],son[100001],bq[100001];
bool vis[100001];
void adeg(int u,int v,int w)
{
  pre[++eg] = now[u];
  now[u] = eg;
  son[eg] = v;
  bq[eg] = w;
}
int n,ans,maxn = 0;
struct bl
{
  int x,y,wl,z;
}bll[10001];
void dfs(int beg,int fa)
{
bll[beg].z = bll[beg].wl;
  vis[beg] = 1;
  for(int i = now[beg]; i; i = pre[i])
  {
      int v = son[i];
      if(v == fa || vis[v]) continue;
      dfs(v,beg);
      if(bll[v].z > 0) bll[beg].z += bll[v].z;
  }
}
signed main()
{
  cin>>n;
  for(int i = 1;i <= n;i++) cin>>bll[i].x>>bll[i].y>>bll[i].wl;
  for(int i = 1;i <= n;i++)
    for(int j = i + 1;j <= n;j++)
      if(abs(bll[i].x - bll[j].x) + abs(bll[i].y - bll[j].y) == 1)
      {
        adeg(i,j,1); 
        adeg(j,i,1);
      }
  dfs(1,0);
  for(int i = 1;i <= n;i++) maxn = max(maxn,bll[i].z);
  cout<<maxn;
  return 0;
}