​定义：令U={u0,u1,…,um}是一个单调不减的实数序列，即ui≤ui+1，i=0，1，…，m-1。其中，ui称为节点，U称为节点矢量，用Ni,p(u)表示第i个p次（p+1阶）B样条基函数，其定义为

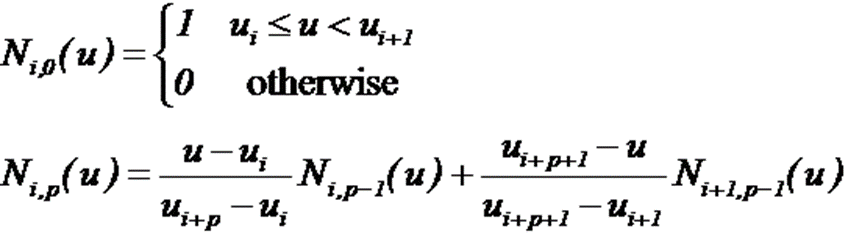
由此可知：

（1）Ni,0(u)是一个阶梯函数，它在半开区间u∈[ui,ui+1)外都为零；

（2）当p>0时，Ni,p(u)是两个p-1次基函数的线性组合；

（3）计算一组基函数时需要事先制定节点矢量U和次数p；

（4）定义式中可能出现0/0，我们规定0/0=0；

（5）Ni,p(u)是定义在整个实数轴上的分段多项式函数，但我们一般只对它在区间[u0,um]上的部分感兴趣；

（6）半开区间[ui,ui+1)称为第i个节点区间（knot span），它的长度可以为零，因为相邻节点可以是相同的；

（7）计算p次基函数的生成过程生成一个如下形式的三角形阵列：

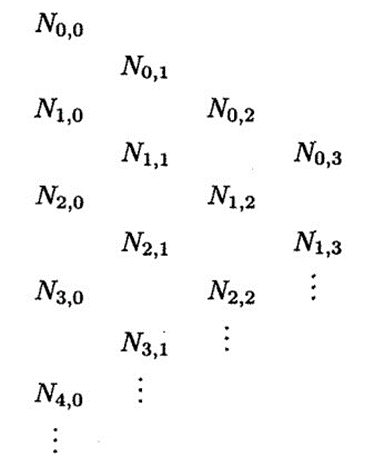
为了书写方便，我们通常将Ni,p(u)写为Ni,p。

性质：

（1）（局部支撑性）如果u∉[ui,ui+p+1)，则Ni,p(u)=0。

（2）在任意给定的节点区间[uj,uj+1)内，最多p+1个Ni,p是非零的，它们是Nj-p,p，…，Nj,p。

（3）（非负性）对于所有的i，p和u，有Ni,p(u)≥0。

（4）（规范性）对于任意的节点区间[ui,ui+1)，当u∈[ui,ui+1)时

（5）（可微性）在节点区间内部，Ni,p(u)是无限次可微的。

（6）除p=0的情况外，Ni,p(u)严格地达到最大值一次。

#include<iostream>
int FindSpan(int n,int p,double u,double* U)
/*
    计算参数u所在区间的下标
    返回参数u所在节点区间的下标,即u所在的区间[ui,ui+1]的i
    U=[u0,u1,u2,...,um]
    n：节点数组最大下标-1,n=m-1
    p：次数
    u：参数
    U：节点数组
    */
{
    if(u==U[n+1])
    {
        return n;
    }
    int low=p;
    int high=n+1;
    int mid=(low+high)/2;
    while(u<U[mid] or u>=U[mid+1])
    {
        if(u<U[mid])
        {
            high=mid;
        }
        else
        {
            low=mid;
        }
        mid=(low+high)/2;
    }
    return mid;
}
void BasisFuns(int i,double u,int p,double* U,double* N)
/*
    计算非零B样条基函数的值
    i:参数u所在节点区间的下标,即u所在的区间[ui,ui+1]的i
    p：次数
    u：参数
    U：节点数组
    N：B样条基函数值数组N(i,i-p),...,N(i,p)
    */
{
    double temp=0.0;
    double saved=0.0;
    double left[p+1];
    double right[p+1];
    N[0]=1.0;
    for(int j=1;j<=p;j++)
    {
        left[j]=u-U[i+1-j];
        right[j]=U[i+j]-u;
        saved=0.0;
        for(int r=0;r<j;r++)
        {
            temp=N[r]/(right[r+1]+left[j-r]);
            N[r]=saved+right[r+1]*temp;
            saved=left[j-r]*temp;
        }
        N[j]=saved;
    }
}
int main()
{
    int n=10;
    const int p=2;
    double u=5.0/2;
    double U[]={0,0,0,1,2,3,4,4,5,5,5};
    double N[p+1];
    BasisFuns(4,u,p,U,N);
    std::cout<<FindSpan(n,p,u,U)<<std::endl;
    for(int i=0;i<=p;i++)
    {
        std::cout<<N[i]<<std::endl;
    }
    system("pause");
}
​