第十二章 计算学习理论(下)
- 12.4 VC 维(Vapnik-Chervonenkis dimension)
- 12.4.1 什么是 VC 维
- 12.4.2 增长函数(growth function)、对分(dichotomy)和打散(shattering)
- 12.5 Rademacher 复杂度
- 12.5.1 引入 Rademacher 复杂度
- 12.5.2 定义、定理、引理
- 12.6 稳定性
- 12.6.1 什么是稳定性
- 12.6.2 泛化损失、经验损失、留一损失
- 12.6.3 定义 12.10
- 12.6.4 定理 12.8
- 12.6.5 经验风险最小化(Empirical Risk Minimization, ERM)
- 12.6.6 定理 12.9
- 12.7 总结
12.4 VC 维(Vapnik-Chervonenkis dimension)
12.4.1 什么是 VC 维
VC维 是统计学和机器学习中的一个概念,用于衡量一个假设类(hypothesis class)的表示能力或复杂性。VC维描述了这个假设类可以拟合的样本集的最大大小,使得该假设类可以实现所有可能的二分类标签的组合。
12.4.2 增长函数(growth function)、对分(dichotomy)和打散(shattering)
增长函数 应该是最容易理解的,但是这里我还是摘抄一下原文给出的数学定义。
给定假设空间 H \mathcal{H} H 和示例集 D = { x 1 , x 2 , . . . , x m } D=\{\bm{x}_1,\bm{x}_2,...,\bm{x}_m\} D={x1,x2,...,xm}, H \mathcal{H} H 中每个假设 h h h 都能对 D D D 中示例赋予标记,标记结果可表示为
h ∣ D = { ( h ( x 1 ) , h ( x 2 ) , … , h ( x m ) ) } \left.h\right|_D=\left\{\left(h\left(\boldsymbol{x}_1\right), h\left(\boldsymbol{x}_2\right), \ldots, h\left(\boldsymbol{x}_m\right)\right)\right\} h∣D={(h(x1),h(x2),…,h(xm))}
随着 m m m 的增大, H \mathcal{H} H 中所有假设对 D D D 中的示例所能赋予标记的可能结果数也会增大。
定义 12.6 对所有 m ∈ N m \in \mathbb{N} m∈N,假设空间 H \mathcal{H} H 的增长函数 Π H ( m ) \Pi_{\mathcal{H}}(m) ΠH(m) 为
Π H ( m ) = max { x 1 , … , x m } ⊆ X ∣ { ( h ( x 1 ) , … , h ( x m ) ) ∣ h ∈ H } ∣ (12.21) \Pi_{\mathcal{H}}(m)=\max _{\left\{\boldsymbol{x}_1, \ldots, \boldsymbol{x}_m\right\} \subseteq \mathcal{X}}\left|\left\{\left(h\left(\boldsymbol{x}_1\right), \ldots, h\left(\boldsymbol{x}_m\right)\right) \mid h \in \mathcal{H}\right\}\right| \tag{12.21} ΠH(m)={x1,…,xm}⊆Xmax∣{(h(x1),…,h(xm))∣h∈H}∣(12.21)
增长函数 Π H ( m ) \Pi_{\mathcal{H}}(m) ΠH(m) 表示假设空间 H \mathcal{H} H 对 m m m 个示例所能赋予标记的最大可能结果数。显然, H \mathcal{H} H 对示例所能赋予标记的可能结果数越大, H \mathcal{H} H 的表示能力越强,对学习任务的适应能力也越强。
因此,增长函数描述了假设空间 H \mathcal{H} H 的表示能力,由此反映出假设空间的复杂度。
定理 12.2 对假设空间 H \mathcal{H} H, m ∈ N m\in \mathbb{N} m∈N, 0 < ϵ < 1 0<\epsilon<1 0<ϵ<1 和任意 h ∈ H h \in \mathcal{H} h∈H 有
P ( ∣ E ( h ) − E ^ ( h ) ∣ > ϵ ) ⩽ 4 Π H ( 2 m ) exp ( − m ϵ 2 8 ) (12.22) P(|E(h)-\widehat{E}(h)|>\epsilon) \leqslant 4 \Pi_{\mathcal{H}}(2 m) \exp \left(-\frac{m \epsilon^2}{8}\right) \tag{12.22} P(∣E(h)−E (h)∣>ϵ)⩽4ΠH(2m)exp(−8mϵ2)(12.22)
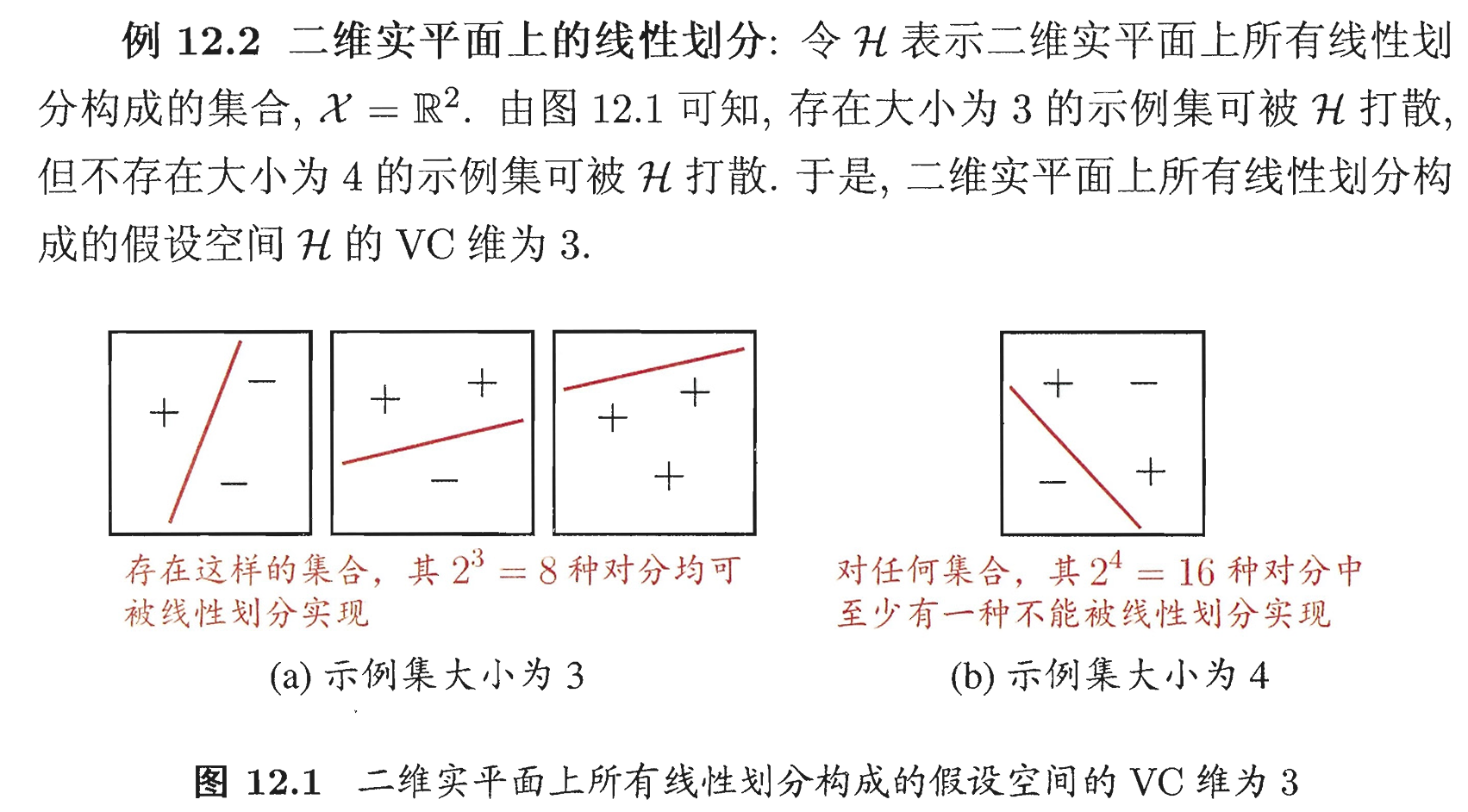
假设空间 H \mathcal{H} H 中不同的假设对于 D D D 中示例赋予标记的结果可能相同,也可能不同;尽管 H \mathcal{H} H 可能包含无穷多个假设,但其对 D D D 中示例赋予标记的可能结果数是有限的:对 m m m 个示例,最多有 2 m 2^m 2m 个可能结果。对二分类问题来说, H \mathcal{H} H 中的假设对 D D D 中示例赋予标记的每种可能结果称为 D D D 的一种 “对分”。若假设空间 H \mathcal{H} H 能实现示例集 D D D 上的所有对分,即 Π H ( m ) = 2 m \Pi_{\mathcal{H}}(m)=2^m ΠH(m)=2m,则称示例集 D D D 能被假设空间 H \mathcal{H} H “打散”。
定理12.2提供了一个关于假设空间 H \mathcal{H} H的期望风险和经验风险之间差距的概率上界。具体来说,它表明当样本容量足够大时,期望风险和经验风险之间的差距不会太大。
定理12.2的条件包括:
- 假设空间 H \mathcal{H} H ;
- 样本容量 m m m ,其中 m m m 是一个自然数;
- 随机变量 ϵ \epsilon ϵ,满足 0 < ϵ < 1 0 < \epsilon < 1 0<ϵ<1;
- 任意的 h ∈ H h \in \mathcal{H} h∈H。
定理12.2的结论是:
- 当样本容量足够大时,期望风险 E ( h ) E(h) E(h)和经验风险 E ^ ( h ) \widehat{E}(h) E (h)之间的差距不大于 ϵ \epsilon ϵ的概率是有限的。
- 具体来说,概率 P ( ∣ E ( h ) − E ^ ( h ) ∣ > ϵ ) P(|E(h) - \widehat{E}(h)| > \epsilon) P(∣E(h)−E (h)∣>ϵ)不超过 4 π H ( 2 m ) exp ( − m ϵ 2 8 ) 4 \pi_{\mathcal{H}}(2m) \exp(-\frac{m\epsilon^2}{8}) 4πH(2m)exp(−8mϵ2)。
这个定理对于机器学习的理论研究和实际应用非常重要。它提供了在随机抽样下,经验风险最小化策略能够保证泛化性能的数学依据。通过控制样本容量和误差 ϵ \epsilon ϵ,我们可以调整概率上界,从而在实际应用中选择合适的样本容量来保证一定的泛化性能。
现在我们可以正式定义 VC 维如下:
定义 12.7 假设空间
H
\mathcal{H}
H 的 VC 维是能被
H
\mathcal{H}
H 打散的最大示例集的大小,即
V
C
(
H
)
=
max
{
m
:
Π
H
(
m
)
=
2
m
}
(12.23)
\mathrm{VC}(\mathcal{H})=\max \left\{m: \Pi_{\mathcal{H}}(m)=2^m\right\} \tag{12.23}
VC(H)=max{m:ΠH(m)=2m}(12.23)
VC ( H ) = d \text{VC}(\mathcal{H})=d VC(H)=d 表明存在大小为 d d d 的示例集能被假设空间 H \mathcal{H} H 打散。
需要注意:
- 并不是所有大小为 d d d 的示例集都能被假设空间 H \mathcal{H} H打散;
- VC 维的定义与数据分布 D \mathcal{D} D 无关,数据分布 D \mathcal{D} D 未知时仍能计算出假设空间 H \mathcal{H} H 的VC维。
通常这样来计算 H \mathcal{H} H 的 VC 维:若存在大小为 d d d 的示例集能被 H \mathcal{H} H 打散,但不存在任何大小为 d + 1 d+1 d+1 的示例集能被 H \mathcal{H} H 打散,则 H \mathcal{H} H 的 VC 维是 d d d。
定义12.6给出了假设空间 H \mathcal{H} H的增长函数 Π H ( m ) \Pi_{\mathcal{H}}(m) ΠH(m)的定义。增长函数描述了随着样本容量 m m m的增加,假设空间 H \mathcal{H} H中可能产生的不同输出值的数量的变化情况。
具体来说,对于给定的样本集 { x 1 , x 2 , … , x m } ⊆ X \{x_1, x_2, \ldots, x_m\} \subseteq \mathcal{X} {x1,x2,…,xm}⊆X,假设空间 H \mathcal{H} H的增长函数 Π H ( m ) \Pi_{\mathcal{H}}(m) ΠH(m)定义为 H \mathcal{H} H中所有可能的输出向量 ( h ( x 1 ) , h ( x 2 ) , … , h ( x m ) ) (h(x_1), h(x_2), \ldots, h(x_m)) (h(x1),h(x2),…,h(xm))的最大数量,其中 h ∈ H h \in \mathcal{H} h∈H。
这个定义反映了随着样本容量的增加,假设空间 H \mathcal{H} H中可能存在的不同输出组合的数量。增长函数的性质对于理解VC维和样本容量的选择有着重要的影响。在机器学习中,我们希望增长函数的值不要增长过快,因为这将导致VC维过大,使得模型过于复杂,容易过拟合。同时,我们也希望增长函数的值不要太小,因为这将限制模型的表达能力,使其无法很好地拟合数据。
引理 12.2 若假设空间 H \mathcal{H} H 的 VC 维为 d d d,则对任意 m ∈ N m\in \mathbb{N} m∈N 有
Π H ( m ) ⩽ ∑ i = 0 d ( m i ) (12.24) \Pi_{\mathcal{H}}(m) \leqslant \sum_{i=0}^d\left(\begin{array}{c} m \\i \end{array}\right) \tag{12.24} ΠH(m)⩽i=0∑d(mi)(12.24)
这个公式涉及到 VC维(VC dimension),这是一个在机器学习理论中常用的术语,用于描述一个假设类的复杂度。VC维是一个假设类能够“划分”(shatter)的最大集合的大小。在这个引理中,它给出了对于具有VC维为 d d d 的假设空间 H \mathcal{H} H,在 m m m 个样本上的划分可能性的上界。
假设我们有一个假设空间 H \mathcal{H} H,它的 VC维为 d = 2 d=2 d=2。这意味着 H \mathcal{H} H 能够划分的最大点集的大小为 2。现在考虑一个包含 3 个点的数据集 S = x 1 , x 2 , x 3 S={x_1, x_2, x_3} S=x1,x2,x3。
根据公式,我们可以计算 H \mathcal{H} H 在 S S S 上的划分可能性:
Π H ( 3 ) ≤ ∑ i = 0 2 ( 3 i ) = ( 3 0 ) + ( 3 1 ) + ( 3 2 ) = 1 + 3 + 3 = 7 \Pi_{\mathcal{H}}(3) \leq \sum_{i=0}^{2}\binom{3}{i} = \binom{3}{0} + \binom{3}{1} + \binom{3}{2} = 1 + 3 + 3 = 7 ΠH(3)≤∑i=02(i3)=(03)+(13)+(23)=1+3+3=7。
这意味着 H \mathcal{H} H 在 S S S 上有最多7种可能的划分方式。实际上,对于VC维为2的假设空间,我们可以列出以下7种划分:
- 将所有点分为同一类。
- 将 x 1 x_1 x1 与 x 2 x_2 x2 分为一类,x3分为另一类。
- 将 x 1 x_1 x1 与 x 3 x_3 x3 分为一类,x2分为另一类。
- 将 x 2 x_2 x2 与 x 3 x_3 x3 分为一类,x1分为另一类。
- 将 x 1 x_1 x1 分为一类, x 2 x_2 x2 与 x 3 x_3 x3 分为另一类。
- 将 x 2 x_2 x2 分为一类, x 1 x_1 x1 与 x 3 x_3 x3 分为另一类。
- 将 x 3 x_3 x3 分为一类, x 1 x_1 x1 与 x 2 x_2 x2 分为另一类。
这些划分展示了 H \mathcal{H} H 在 S S S 上的最大划分能力。这个例子说明了如何使用公式来计算给定假设空间在特定数据集上的划分可能性。
在机器学习理论中,这个公式可以用来分析假设空间的复杂度,以及它对过拟合风险的影响。例如,如果一个假设空间的VC维较小,那么它在训练数据上的划分可能性就有限,这通常意味着模型的泛化性能较好。反之,如果VC维较大,那么模型可能会过度拟合训练数据,导致在新数据上的表现不佳。
右边的求和表示从 0 0 0 到 d d d 的二项式系数之和,其中 ( m i ) \binom{m}{i} (im)表示从 m m m 个元素中选择 i i i 个元素的组合数。这个公式表明,当假设空间的VC维为 d d d 时,最多可以有 ∑ i = 0 d ( m i ) \sum_{i=0}^{d}\binom{m}{i} ∑i=0d(im) 种不同的划分方式。
推论 12.2 若假设空间
H
\mathcal{H}
H 的 VC 维为
d
d
d, 则对任意整数
m
⩾
d
m \geqslant d
m⩾d 有
Π
H
(
m
)
⩽
(
e
⋅
m
d
)
d
(12.28)
\Pi_{\mathcal{H}}(m) \leqslant\left(\frac{e \cdot m}{d}\right)^d \tag{12.28}
ΠH(m)⩽(de⋅m)d(12.28)
根据推论 12.2 和定理 12.2 可得基于 VC 维的泛化误差界:
定理 12.3 若假设空间 H \mathcal{H} H 的 VC 维为 d d d,则对任意 m > d m > d m>d, 0 < δ < 1 0<\delta<1 0<δ<1 和 h ∈ H h\in \mathcal{H} h∈H 有
P ( E ( h ) − E ^ ( h ) ⩽ 8 d ln 2 e m d + 8 ln 4 δ m ) ⩾ 1 − δ (12.29) P\left(E(h)-\widehat{E}(h) \leqslant \sqrt{\frac{8 d \ln \frac{2 e m}{d}+8 \ln \frac{4}{\delta}}{m}}\right) \geqslant 1-\delta \tag{12.29} P E(h)−E (h)⩽m8dlnd2em+8lnδ4 ⩾1−δ(12.29)
由定理 12.3 可知,式 (12.29) 的泛化误差界只与样本数目 m m m 有关,收敛速率为 O ( 1 m ) O(\frac{1}{\sqrt{m}}) O(m1),与数据分布 D D D和样本集 D D D无关。因此,基于VC维的泛化误差界是分布无关(distribution-free)、数据独立(data-independent)的。
定理 12.4 任何 VC 维有限的假设空间 H \mathcal{H} H 都是(不可知)PAC 可学习的。
关于 VC维 、 PAC可学习性、不可知学习 前面章节已经详细介绍,结合以上概念,我们可以理解这句话的意思是:如果一个假设空间 H \mathcal{H} H 的 VC维是有限的,那么存在一个学习算法,可以从有限的训练数据中学习到一个假设,使得该假设在未知的真实数据上的泛化误差(以概率至少为 1 − δ 1-\delta 1−δ)小于 ϵ \epsilon ϵ。这个结论意味着,只要假设空间的复杂度(由VC维衡量)是有限的,那么就可以找到一个学习算法,在多项式时间内从有限的训练数据中学习到一个近似正确的假设。
12.5 Rademacher 复杂度
12.5.1 引入 Rademacher 复杂度
12.4 节提到,基于VC维的泛化误差界是分布无关、数据独立的,也就是说,它对任何数据分布都成立。这使得基于VC维的学习性分析结果具有一定的“普适性”;但另一方面,由于没有考虑数据自身,基于VC维得到的泛化误差界通常比较“松”,对那些与学习问题的典型情况相差甚远的较“坏”分布来说尤其如此。
Rademacher 复杂度是另一种刻画假设空间复杂度的方法,与VC维不同的是,它在一定程度上考虑了数据分布。
12.5.2 定义、定理、引理
Rademacher 复杂度是一个用来衡量假设空间 F \mathcal{F} F 复杂度的概念,它通过随机扰动训练数据来估计一个函数类在实际数据上的期望性能。具体来说,Rademacher复杂度定义如下:
设 Z \mathcal{Z} Z是输入空间, F \mathcal{F} F是一个假设空间, Z = { z 1 , z 2 , … , z m } Z = \{\bm{z}_1, \bm{z}_2, \dots, \bm{z}_m\} Z={z1,z2,…,zm}是从 Z \mathcal{Z} Z 中取样得到的有限训练集。Rademacher 复杂度 R ^ Z ( F ) \hat{R}_Z(\mathcal{F}) R^Z(F)定义为:
R ^ Z ( F ) = E σ [ sup f ∈ F ∣ 1 m ∑ i = 1 m σ i f ( z i ) ∣ ] (12.40) \hat{R}_Z(\mathcal{F}) = \mathbb{E}_{\sigma} \left[ \sup_{f \in \mathcal{F}} \left| \frac{1}{m} \sum_{i=1}^m \sigma_i f(\bm{z}_i) \right| \right] \tag{12.40} R^Z(F)=Eσ[f∈Fsup m1i=1∑mσif(zi) ](12.40)
其中, σ = ( σ 1 , σ 2 , … , σ m ) \sigma = (\sigma_1, \sigma_2, \dots, \sigma_m) σ=(σ1,σ2,…,σm)是一个随机变量序列,每个 σ i \sigma_i σi独立地取值于 { − 1 , 1 } \{-1, 1\} {−1,1}。 R ^ m ( Z ) \hat{R}_m(Z) R^m(Z)表示在随机选择的扰动下,假设空间 F \mathcal{F} F中函数的期望最大偏差。
Rademacher复杂度提供了一种衡量假设空间复杂性的方法,它考虑了数据分布的影响,因为它依赖于训练数据集 S \mathcal{S} S。通过研究Rademacher复杂度,可以更好地理解假设空间的复杂性如何影响学习算法的泛化性能。在机器学习理论中,Rademacher复杂度被广泛用于分析学习算法的性能,特别是在支持向量机(SVM)和神经网络等复杂模型的研究中。
定义 12.9 函数空间 F 关于 Z 上分布 D 的 Rademacher 复杂度
R m ( F ) = E Z ⊆ Z : ∣ Z ∣ = m [ R ^ Z ( F ) ] . (12.41) R_m(\mathcal{F}) = \mathbb{E}_{Z \subseteq \mathcal{Z}: |Z|=m} [ \widehat{R}_Z(\mathcal{F}) ]. \tag{12.41} Rm(F)=EZ⊆Z:∣Z∣=m[R Z(F)].(12.41)
定理 12.5 对实值函数空间 F : Z → [ 0 , 1 ] \mathcal{F}: \mathbb{Z} \rightarrow [0,1] F:Z→[0,1], 根据分布 D \mathcal{D} D 从 Z \mathbb{Z} Z 中独立同分布采样得到示例集 Z = { z 1 , z 2 , … , z m } Z = \{\bm{z}_1, \bm{z}_2, \ldots, \bm{z}_m\} Z={z1,z2,…,zm}, z i ∈ Z z_i \in \mathbb{Z} zi∈Z, 0 < δ < 1 0 < \delta < 1 0<δ<1, 对任意 f ∈ F f \in \mathcal{F} f∈F, 以至少 1 − δ 1-\delta 1−δ 的概率有
E
[
f
(
z
)
]
⩽
1
m
∑
i
=
1
m
f
(
z
i
)
+
2
R
m
(
F
)
+
ln
(
1
/
δ
)
2
m
(12.42)
\mathbb{E}[f(\boldsymbol{z})] \leqslant \frac{1}{m} \sum_{i=1}^m f\left(\boldsymbol{z}_i\right)+2 R_m(\mathcal{F})+\sqrt{\frac{\ln (1 / \delta)}{2 m}} \tag{12.42}
E[f(z)]⩽m1i=1∑mf(zi)+2Rm(F)+2mln(1/δ)(12.42)
其中,
1
m
∑
i
=
1
m
f
(
z
i
)
\frac{1}{m} \sum_{i=1}^m f(z_i)
m1∑i=1mf(zi) 是经验均值,
R
m
(
F
)
R_m(\mathcal{F})
Rm(F) 是经验风险上界,而
ln
(
1
/
δ
)
2
m
\sqrt{\frac{\ln(1/\delta)}{2m}}
2mln(1/δ) 是一个随机项,它与置信水平
δ
\delta
δ 相关。
E [ f ( z ) ] ⩽ 1 m ∑ i = 1 m f ( z i ) + 2 R ^ Z ( F ) + 3 ln ( 2 / δ ) 2 m (12.43) \mathbb{E}[f(\boldsymbol{z})] \leqslant \frac{1}{m} \sum_{i=1}^m f\left(\boldsymbol{z}_i\right)+2 \widehat{R}_Z(\mathcal{F})+3 \sqrt{\frac{\ln (2 / \delta)}{2 m}} \tag{12.43} E[f(z)]⩽m1i=1∑mf(zi)+2R Z(F)+32mln(2/δ)(12.43)
其中, 1 m ∑ i = 1 m f ( z i ) \frac{1}{m} \sum_{i=1}^m f(z_i) m1∑i=1mf(zi) 是经验均值, R ^ Z ( F ) \widehat{R}_Z(\mathcal{F}) R Z(F) 是经验风险上界,而 ln ( 2 / δ ) 2 m \sqrt{\frac{\ln(2/\delta)}{2m}} 2mln(2/δ) 是一个随机项,它与置信水平 δ \delta δ 相关。
定理 12.5 提供了对实值函数空间 F : Z → [ 0 , 1 ] \mathcal{F} : \mathbb{Z} \to [0, 1] F:Z→[0,1] 上的期望函数 E [ f ( z ) ] \mathbb{E}[f(z)] E[f(z)] 的上界,其中 z ∈ Z z \in \mathbb{Z} z∈Z, 0 < δ < 1 0 < \delta < 1 0<δ<1,并且样本集 Z = { z 1 , z 2 , … , z m } Z = \{z_1, z_2, \dots, z_m\} Z={z1,z2,…,zm} 是根据分布 D \mathcal{D} D 从 Z \mathbb{Z} Z 中独立同分布采样的。定理保证了对于任意的 f ∈ F f \in \mathcal{F} f∈F,至少有概率 1 − δ 1 - \delta 1−δ 满足以下两个不等式:
这两个不等式都涉及到经验风险上界和随机项,它们反映了经验风险和期望风险之间的关系。这些不等式对于理解和估计未知分布上的期望函数具有重要意义,特别是在有限样本的情况下。通过这些不等式,我们可以获得关于期望函数的一个上界,从而对未知分布有一个更好的估计。
定理 12.6 对假设空间 H : X → { − 1 , + 1 } \mathcal{H}: \mathcal{X} \to \{-1,+1\} H:X→{−1,+1},根据分布 D \mathcal{D} D 从 X \mathcal{X} X 中独立同分布采样得到样本集 D = { x 1 , x 2 , … , x m } \mathcal{D} = \{\bm{x}_1, \bm{x}_2, \dots, \bm{x}_m\} D={x1,x2,…,xm}, x i ∈ X \bm{x}_i \in \mathcal{X} xi∈X, 0 < δ < 1 0 < \delta < 1 0<δ<1,对任意 h ∈ H h \in \mathcal{H} h∈H,以至少 1 − δ 1 - \delta 1−δ 的概率有
E ( h ) ≤ E ^ ( h ) + R m ( H ) + ln ( 1 / δ ) 2 m (12.47) E(h) \leq \hat{E}(h) + R_m(\mathcal{H}) + \sqrt{\frac{\ln(1/\delta)}{2m}} \tag{12.47} E(h)≤E^(h)+Rm(H)+2mln(1/δ)(12.47)
E ( h ) ≤ E ^ ( h ) + R ^ D ( H ) + 3 ln ( 2 / δ ) 2 m (12.48) E(h) \leq \hat{E}(h) + \widehat{R}_D(\mathcal{H}) + 3\sqrt{\frac{\ln(2/\delta)}{2m}} \tag{12.48} E(h)≤E^(h)+R D(H)+32mln(2/δ)(12.48)
这个定理给出了在假设空间 H \mathcal{H} H 中,当从分布 D \mathcal{D} D 中独立同分布采样得到样本集 D \mathcal{D} D 时,期望函数 E ( h ) E(h) E(h) 的上界。定理中的两个不等式分别考虑了经验风险 R m ( H ) R_m(\mathcal{H}) Rm(H) 和分布风险 R ^ D ( H ) \widehat{R}_D(\mathcal{H}) R D(H) 的情况。
基于 Rademacher 复杂度的泛化误差界依赖于具体学习问题上的数据分布,有点类似于为该学习问题“量身定制”的,因此它通常比基于 VO 维的泛化误差界更紧一些.
定理 12.7 假设空间 H \mathcal{H} H 的 Rademacher 复杂度 R m ( H ) R_m(\mathcal{H}) Rm(H) 与增长函数 Π H ( m ) \Pi_{\mathcal{H}}(m) ΠH(m) 满足:
R m ( H ) ⩽ 2 ln Π H ( m ) m (12.52) R_m(\mathcal{H}) \leqslant \sqrt{\frac{2\ln \Pi_{\mathcal{H}}(m)}{m}} \tag{12.52} Rm(H)⩽m2lnΠH(m)(12.52)
这个定理给出了假设空间 H \mathcal{H} H 的 Rademacher 复杂度 R m ( H ) R_m(\mathcal{H}) Rm(H) 与增长函数 Π H ( m ) \Pi_{\mathcal{H}}(m) ΠH(m) 之间的关系。根据公式 ( 12.52 ) (12.52) (12.52),Rademacher 复杂度被上界为增长函数的对数的平方根除以样本数量。
12.6 稳定性
12.6.1 什么是稳定性
12.6.2 泛化损失、经验损失、留一损失
泛化损失 刻画了假设 L D \mathfrak{L}_D LD 的预测标记 L D ( x ) \mathfrak{L}_D(\bm{x}) LD(x) 与真实标记 y y y 之间的差别,简记为 ℓ ( L D , z ) \ell(\mathfrak{L}_D,\bm{z}) ℓ(LD,z)。
ℓ ( L , D ) = E x ∈ X , z = ( x , y ) [ ℓ ( L D , z ) ] (12.54) \ell(\mathfrak{L}, \mathcal{D}) = \mathbb{E}_{\bm{x} \in \mathcal{X}, \bm{z} = (\bm{x}, y)} [\ell(\mathfrak{L}_D, \bm{z})] \tag{12.54} ℓ(L,D)=Ex∈X,z=(x,y)[ℓ(LD,z)](12.54)
12.6.3 定义 12.10
定义 12.10 对于任何 x ∈ X x \in X x∈X, z = ( x , y ) z = (x, y) z=(x,y), 如果学习算法 L \mathcal{L} L 满足:
∣ l ( L D , z ) − l ( L D ∖ i , z ) ∣ ≤ β , i = 1 , 2 , … , m , (12.57) |l(\mathfrak{L}_D, z) - l(\mathfrak{L}_{D \setminus i}, z)| \leq \beta, \; i = 1, 2, \ldots, m, \tag{12.57} ∣l(LD,z)−l(LD∖i,z)∣≤β,i=1,2,…,m,(12.57)
则称 L \mathfrak{L} L 关于损失函数 l l l 满足 β \beta β-均匀稳定性。
这里, L D \mathcal{L}_D LD 表示使用数据集 D D D 训练得到的学习器,而 L D ∖ i \mathcal{L}_{D \setminus i} LD∖i 表示使用除了第 i i i 个样本外的数据集 D D D 训练得到的学习器。
12.6.4 定理 12.8
定理 12.8 给定从分布 D \mathcal{D} D 上独立同分布采样得到的大小为 m m m 的示例集 D D D,若学习算法 L \mathfrak{L} L 满足关于损失函数 ℓ \ell ℓ 的 β \beta β-均匀稳定性,且损失函数 ℓ \ell ℓ 的上界为 M M M, 0 < δ < 1 0 < \delta < 1 0<δ<1,则对任意 m ≥ 1 m \geq 1 m≥1,以至少 1 − δ 1 - \delta 1−δ 的概率有
ℓ ( L , D ) ⩽ ℓ ^ ( L , D ) + 2 β + ( 4 m β + M ) ln ( 1 / δ ) 2 m (12.58) \ell(\mathfrak{L}, \mathcal{D}) \leqslant \hat{\ell}(\mathfrak{L}, \mathcal{D}) + 2\beta + \left(4m\beta + M\right)\sqrt{\frac{\ln(1/\delta)}{2m}} \tag{12.58} ℓ(L,D)⩽ℓ^(L,D)+2β+(4mβ+M)2mln(1/δ)(12.58)
ℓ ( L , D ) ⩽ ℓ l o o ( L , D ) + β + ( 4 m β + M ) ln ( 1 / δ ) 2 m (12.59) \ell(\mathfrak{L}, \mathcal{D}) \leqslant \ell_{loo}(\mathfrak{L}, \mathcal{D}) + \beta + \left(4m\beta + M\right)\sqrt{\frac{\ln(1/\delta)}{2m}} \tag{12.59} ℓ(L,D)⩽ℓloo(L,D)+β+(4mβ+M)2mln(1/δ)(12.59)
这个定理给出了学习算法 L \mathfrak{L} L 在满足 β \beta β-均匀稳定性和损失函数 ℓ \ell ℓ 的上界为 M M M 的情况下,对于任意大小为 m m m 的示例集 D \mathcal{D} D,以至少 1 − δ 1 - \delta 1−δ 的概率,其损失函数 ℓ \ell ℓ 的上界。
12.6.5 经验风险最小化(Empirical Risk Minimization, ERM)
对损失函数 ℓ \ell ℓ,若学习算法 L \mathfrak{L} L 所输出的假设满足经验损失最小化,则称算法 L \mathfrak{L} L 满足 经验风险最小化 (Empirical Risk Minimization) 原则,简称算法是 ERM 的。
在机器学习中,结构风险是一个模型的复杂度与泛化误差之间的权衡。它是指一个模型在处理未知数据时可能产生的预测误差,即模型在新数据上的表现。结构风险通常包括模型的复杂度和训练数据的噪声等因素。
结构风险最小化(Structured Risk Minimization, SRM)是一种机器学习中的学习策略,它试图找到一个既能很好地拟合训练数据又能保持低复杂度的模型。简单来说,结构风险最小化的目标是在训练误差和模型复杂度之间取得平衡,以获得更好的泛化能力。
与经验风险最小化(Empirical Risk Minimization, ERM)不同,经验风险最小化只关注模型在训练数据上的表现,而结构风险最小化考虑了模型的复杂度,试图避免过拟合问题。通过引入正则化项或其他复杂度惩罚机制,结构风险最小化可以控制模型的复杂度,从而提高模型在新数据上的性能。
因此,结构风险最小化是一种更全面的学习策略,它不仅考虑了模型在训练数据上的表现,还考虑了模型的复杂度,以提高模型的泛化能力。
12.6.6 定理 12.9
定理 12.9 若学习算法 L \mathfrak{L} L 是 ERM 且稳定的,则假设空间 H \mathcal{H} H 可学习。
12.7 总结
从 PAC 学习到 VC 维,再到 Rademacher 复杂度,最后以稳定性收尾,这些都纯属理论研究,对于绝大多数人来说,非常的无趣且乏味。尤其是使用一堆符号进行推导,最后得出其他的符号表达式的过程中。
篇幅+本人能力有限,这里完全不含任何定理的推导过程。主要想描述一下有这个定义、定理、推论存在,并且希望自己能理解并将自己的理解记录下来。
理论研究是推动创建的基础,并且指导着实际活动,有助于我们深入理解现象的本质和规律。愿你们也能在被一堆符号惹恼以后能够感受它们的魅力 ~
Smileyan
2024.01.31 23:06