主成分分析PCA

- 2D示例

首先，只考虑两个维度的数据集，比如高度和重量。这个数据集可以绘制成平面上的点。但如果想要整理出变量，PCA会找到一个新的坐标系，其中每个点都有一个新的(x,y)值。坐标轴实际上没有任何物理意义。它们是高度和重量的组合，被称为“主分量”。

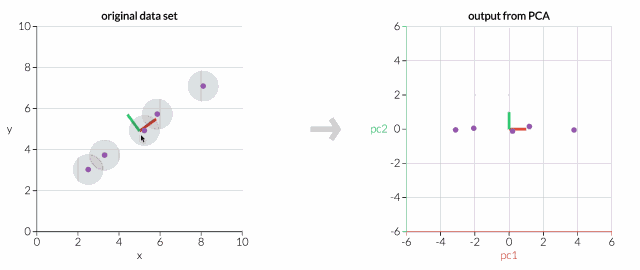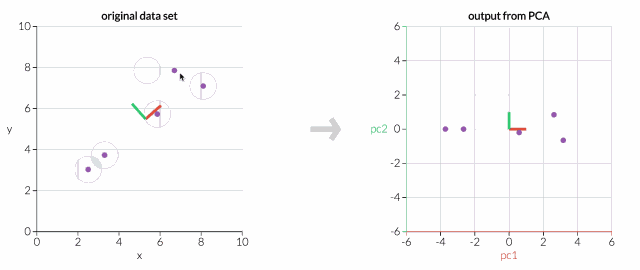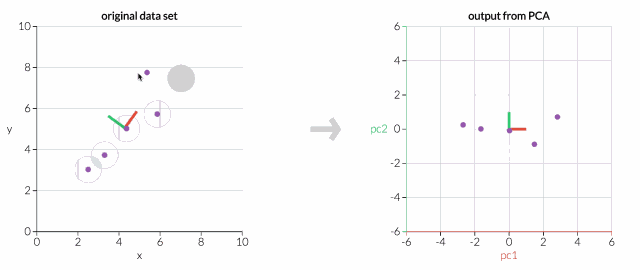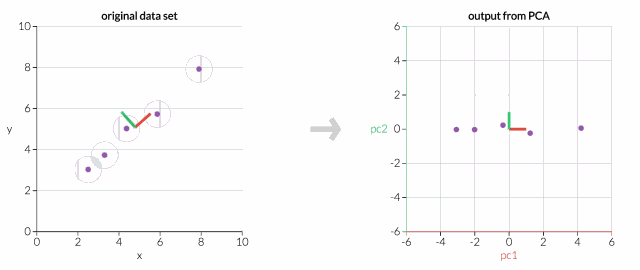
拖动原始数据集中的点，可以看到PC坐标系统正在调整

PCA对于降维很有用。下面，我们将数据绘制成两条直线:一条由x值组成，另一条由y值组成。

但是，如果我们只打算沿一个维度查看数据，那么将该维度作为具有最大变化的主成分可能会更好。通过减少PC2，不会造成太大损失，因为它对数据集的变化贡献最小。

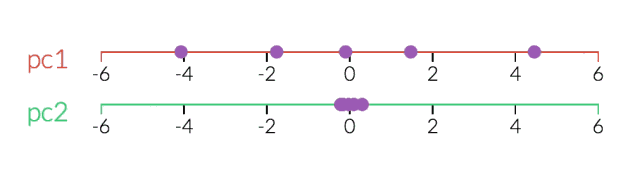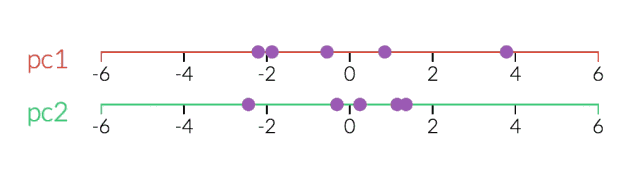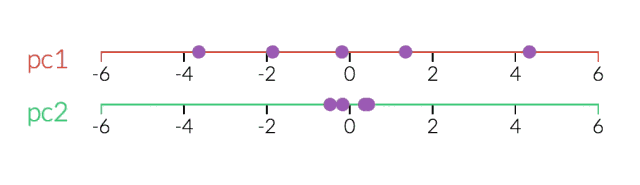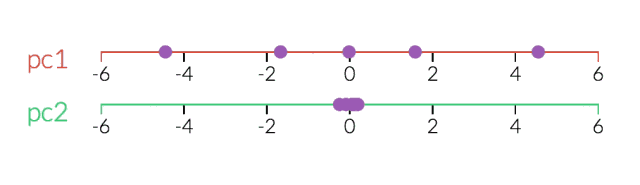
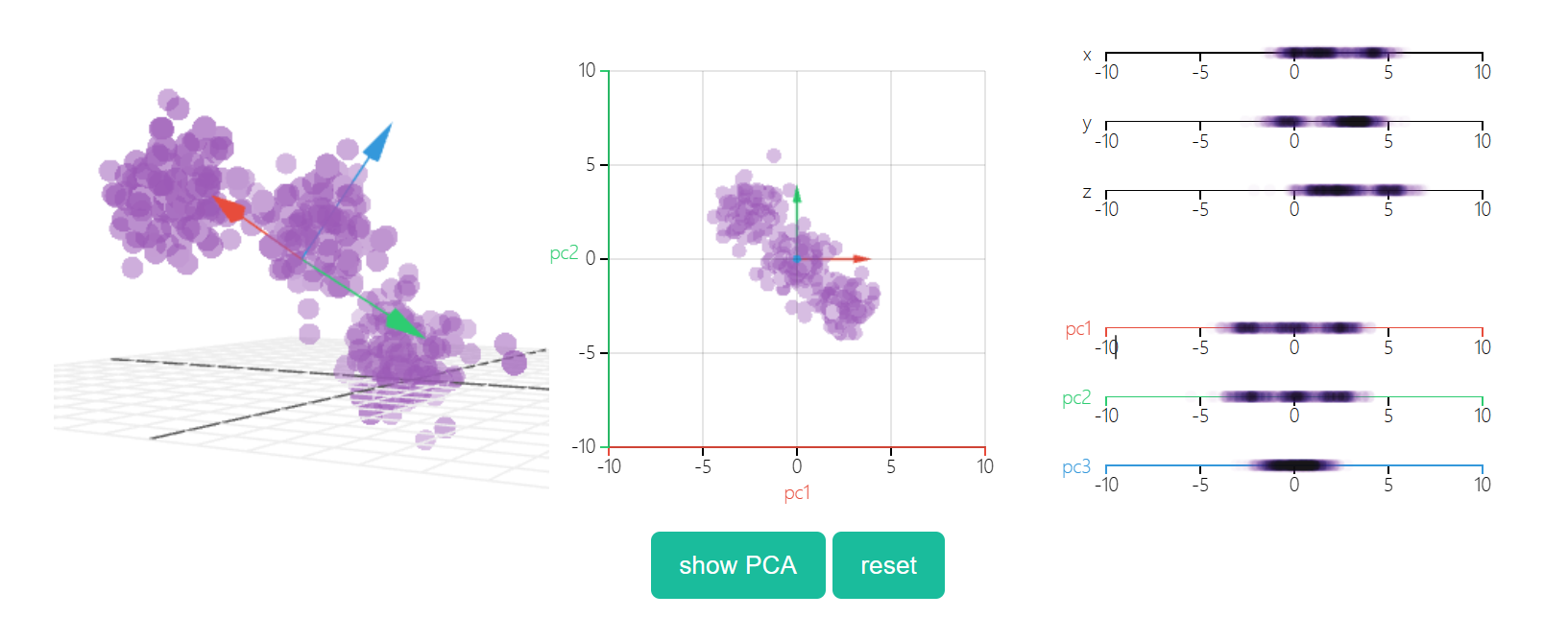
- 3D示例

看透一个数据云是非常困难的，因此，在3D空间中，PCA显得更为重要。在下面的示例中，原始数据以3D的形式绘制，但可以通过不同的视角，将其投射到2D空间。确定好角度之后，点击“显示PCA”按钮，即可呈现2D的结果。在本例中，PCA变换确保水平轴PC1的变化量最大，垂直轴PC2的变化量次之，第三轴PC3的变化量最少。显然，PC3是丢弃的。

- 应用：吃喝在英国

如果数据集不仅仅是三维的，而是17个维度的呢？！如下表所示：

表中是英国每个地区平均每人每周17种食物的消费量，单位为克。这张表显示了不同食物类型之间存在的一些有趣的差异，但总体差异并不显著。让我们看看PCA是否可以通过降维来强地区家之间的差异。

下图是第一个主成分的数据图。我们可以看到一些有关北爱尔兰的情况已经发生了变化。

现在，看看第一和第二主成分，可以看到北爱尔兰是一个主要的异常值。一旦回过头来看看表格中的数据，这就显得很有道理了:北爱尔兰人吃的新鲜土豆要很多，吃的新鲜水果、奶酪、鱼和酒精饮料较少。这是一个很好的迹象，我们所看到的结构反映了现实世界地理的一个重要事实北爱尔兰是四个国家中唯一一个不在大不列颠岛上的。

条件概率

条件概率是指一个事件在另外一个事件已经发生条件下的发生概率。一个落下来的球可能落在红色的架子上(称之为A事件)，或者落在蓝色架子上(称之为B事件)，或者两者兼而有之。

那么给定一个球，它击中了红色架子（A事件），而后击中蓝色架子（B事件）的概率会是多少呢？可以通过给定A的条件概率，即P（B | A）来回答这个问题。

普通最小二乘法回归

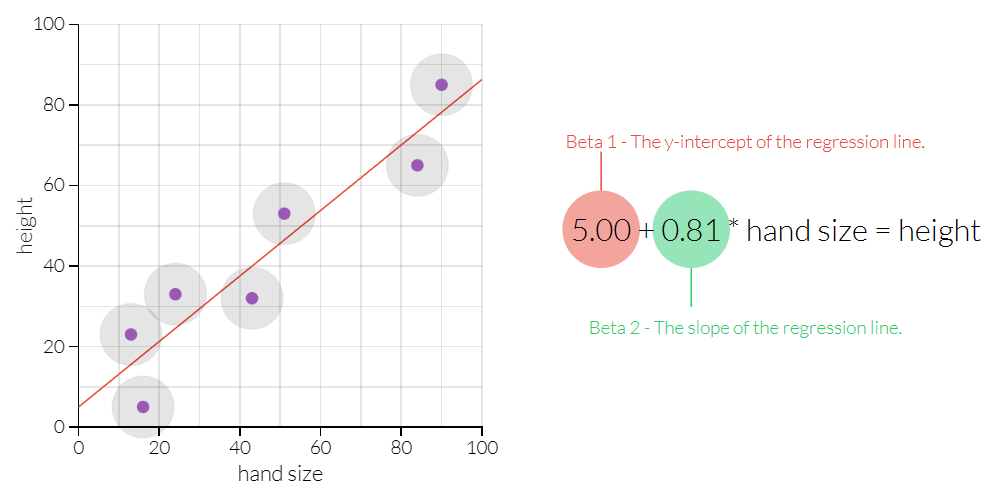
统计回归基本上是一种从一批现有数据中预测未知数量的方法。例如，假设我们一开始就知道 "样本人口 "中一群人的身高和手掌大小，并且我们想找出一种方法，从身高预测不在样本中的人的手掌大小。通过应用OLS，我们将得到一个方程，将手的大小--"自变量 "作为输入，而将身高--"因变量 "作为输出。

下面，OLS是在幕后进行的，以产生回归方程。回归中的常数--即所谓的 "betas"--是OLS吐出的东西。在这里，beta_1是一个截距；它告诉人们即使手的尺寸为零，身高也会是多少。而β_2是手掌大小的系数；它告诉我们，在手掌大小给定的情况下，我们应该期望某人能长多高。拖动样本数据，看看贝塔的变化。