时钟说明

primary clock 基准时钟，primary这里有“基本的”更贴切，虽然其有“主要的、首要的、初级的、原发性的”意思。

提供的基准时钟有俩种情况：

• 时钟由外部时钟源提供，通过输入引脚进入FPGA；
• 高速收发器(GT)的时钟RXOUTCLK或TXOUTCLK；

注：对于7系列FPGA，需要对GT的这俩个时钟手工约束；对于UltraScale FPGA,只需要对GT的输入时钟约束即可。

约束用到的TCL命令：

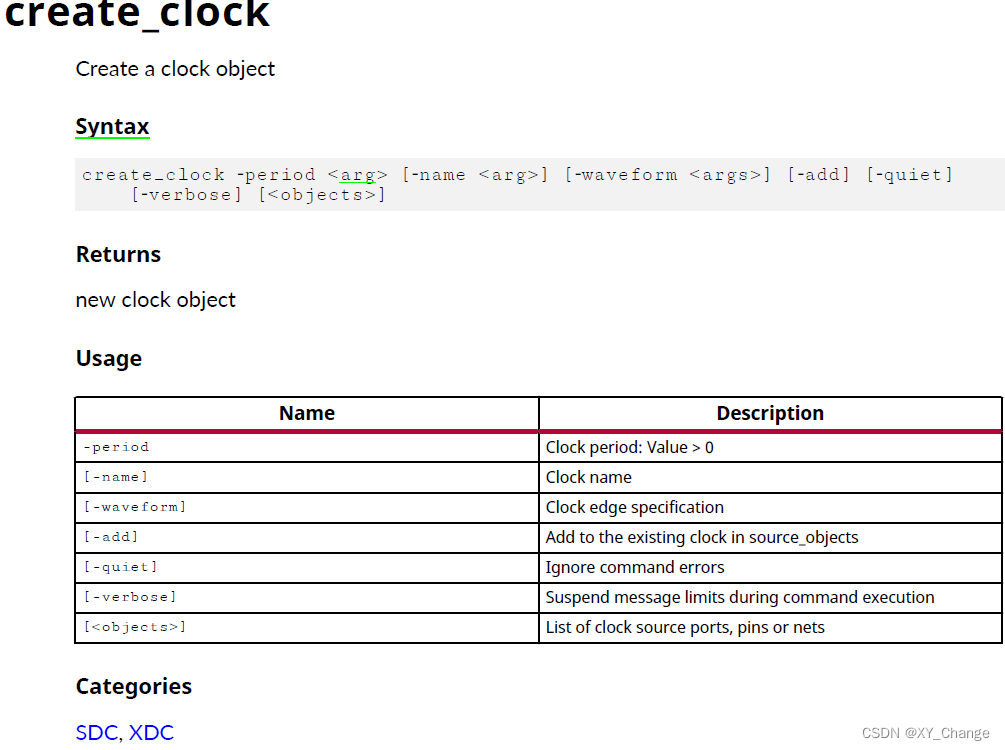
对于此create_clock命令，可以定义基准时钟（时序分析的起点），也可以定义虚拟时钟。
虚拟时钟在设计里没有源头，虚拟时钟是用作输入输出延迟时使用，但是在设计里并不是物理存在。
那么，对于一个物理真实存在的时钟也可以生成一个新时钟，并且这个新时钟可以从主时钟那派生出它的许多属性，用的命令是 create_generated_clock 。
要注意，如果你使用create_clock命令而不是用create_generated_clock命令来创建一个“生成时钟”，新创建的这个时钟不继承源时钟的任何属性。那么将导致内部插入的母时钟延迟和抖动不会传播给生成的时钟，这就会导致错误的时序分析。

命令解析：

-period <arg>

必须要的，是指定被创建的时钟对象的周期，以纳秒为单位，值必须大于0；

-name <arg>

可选的，被创建的时钟对象的名字。如果你省略了名字，系统就会通过被定义的源头“”来生成名字。你当然可以不通过源"< objects >"，用“-name”来自己命名。对于创建设计中没有物理源头的虚拟时钟时，你肯定要选“-name< arg >”,因为虚拟时钟是无“< objects >”，所以才需自己创建。

-waveform <arg1 arg2 ...>

可选的，指定时钟的上升沿和下降沿时间，以纳秒为单位，要覆盖到一个整时钟周期才行。你可以使用多个上升沿和下降沿来定义波形的特征，但是边沿数必须是偶数值，这样才能把波形俩个边沿都表征出来。第一个指定的时间"arg1"代表第一个上升过渡时间，第二个参数“arg2”指随之而来的下降沿。如果下降沿的值小于上升沿的值，意味着下降沿出现在上升沿之前。若是不指定波形，系统会默认波形上升沿在时刻0.0ns，下降沿是指定周期的一半的时间时刻。

-add

可选的，在同一源上定义不同的时钟波形，以同时分析不同的时钟波形。用“-name”来指定添加的新的时钟。若你不对此操作进行说明（即不用-add操作），那么 create_clock 命令将覆盖掉已经存在的时钟名字。

-quiet

可选的，安静的执行命令，不从命令台返回任何消息。命令台会返回TCL_OK，而不是任何在执行过程遇到的错误。

-verbose

可选的，临时解除任何消息限制，并且从命令台返回所有信息。verbose有详细的意思。注：消息限制可以由set_msg_config命令来进行定义。

< objects >

可选的，端口、pin脚、网络都可能是这个被定义的时钟的源。如果你定义一个时钟在一个源对象上，源上已经有一个时钟，新的时钟将覆盖掉原来的时钟，除非你使用“-add”操作。如果没有"< objects >"操作被说明来连接到时钟对象上，被创建的时钟就会被当做虚拟时钟。

未完待续