代码求解next数组

1. KMP相关概念

1. 前缀：包含首位字符但不包含末位字符
2. 后缀：包含末位字符但不包含首位字符
3. next数字：主串与模式串不匹配时，模式串需要回退的位置
4. next[j]：第 j 位字符前面的j-1位字符组成的字串的前后缀重合字符数+1

2. 手算next

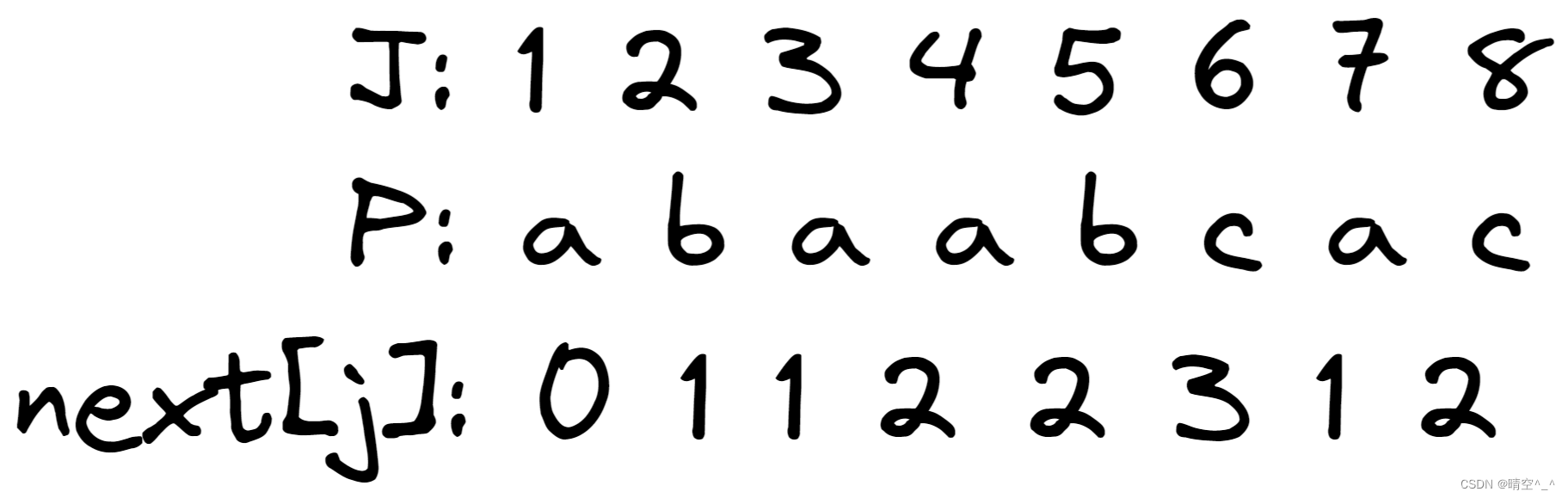
1. 手算过程
   1. j=1，规定next[1] = 0
   2. j=2，子串为a，无对称，next[2] = 1
   3. j=3，子串为ab，无对称，next[3] = 1
   4. j=4，子串aba，对称为a,a，next[4]= 2
   5. j=5，子串abaa，对称为a,a，next[5]=2
   6. j=6，子串abaab，对称ab,ab，next[6]=3
   7. j=7，子串abaabc，无对称，next[7] = 1
   8. j=8，子串abaabca，对称a,a，next[8] = 2
2. 规律：
   1. next数组每次最多加一
   2. 模式串最后一位字符不影响next数组的结果

3. 代码计算

1. 图解：

   1. 求next[9]，则next[8]已知。如图，假设next[8]=4。
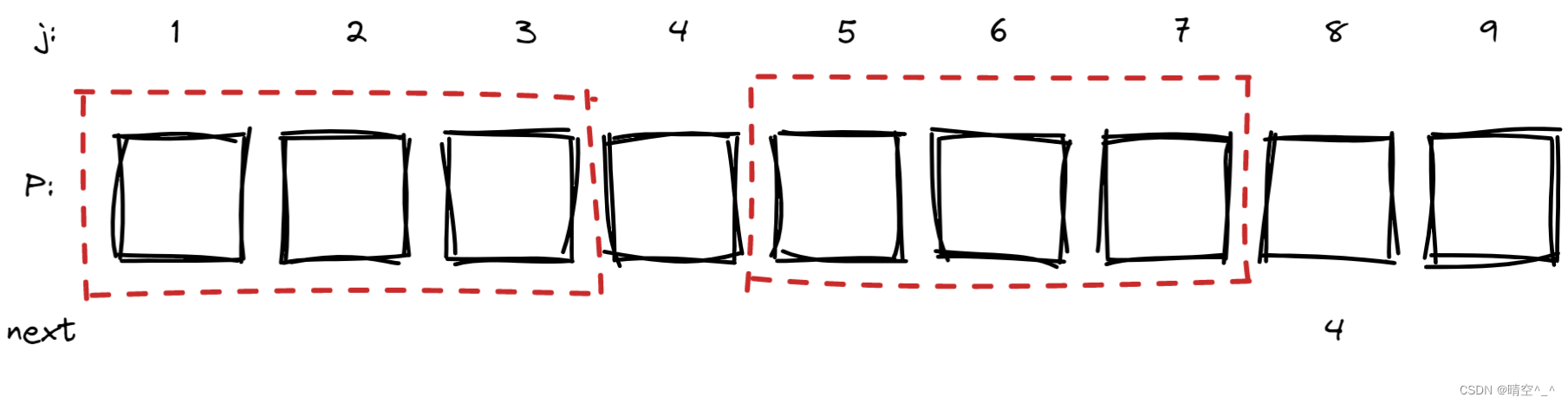
      则模式串中next[1-3]与next[5-7]一定相等（手算next也是这么算的）。

   2. 若p[8]==p[4]，则证明p[1-4]与p[5-8]相等，则next[9]=next[8]+1=5。（最理想）

   3. 若p[8]!=p[4]，则看next[4]，假设next[4]=2。

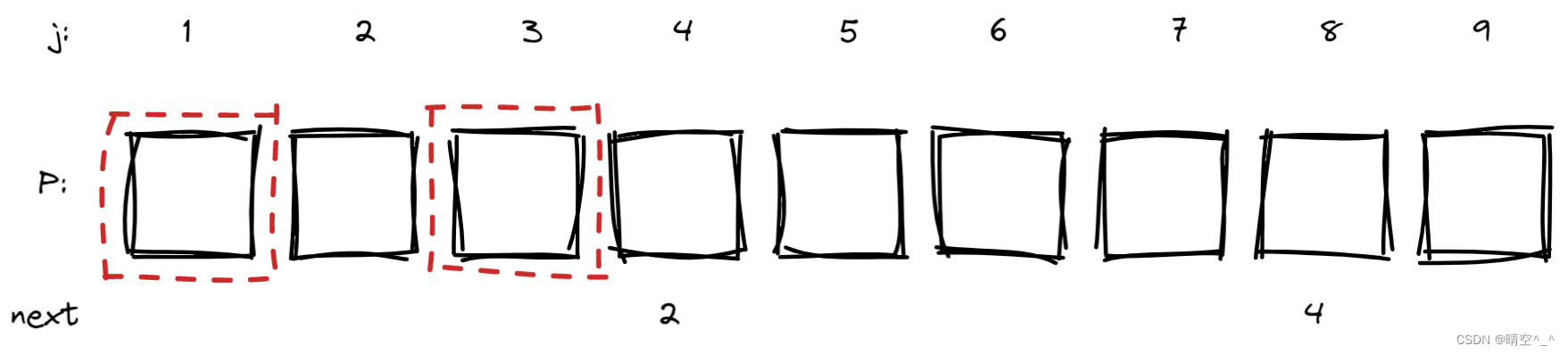      则模式串p[1]与p[3]一定相等 。

   4. 若p[8]==p[2]，则next[9]=next[4]+1=3

   5. 若p[8]!=p[2]，则看next[2]=1

   6. next[1]=0，遇到0还没出现结果，则递推结束，next[9]=1

2. 代码：

   void GetNext(char ch[], int length, int next[]){
       next[1] = 0; // 规定
       // i: next数组的索引
       // j: 模式串的索引
       int i = 1, j = 0;  
       while(i <= length){
           if(j == 0 || ch[i] == ch[j])
               next[++i] = ++j;
            else
                j = next[j];
       }
   }
   

4. 总结：

KMP算法是字符串模式匹配中比较经典的算法，但同时也有一定难度，希望在看完本博客之后，自己 写一个模式串然后利用本代码debug一行一行的跑一遍，相信大家一定会明白的。