⬜⬜⬜ 🐰🟧🟨🟩🟦🟪 (*^▽^*)欢迎光临 🟧🟨🟩🟦🟪🐰⬜⬜⬜
✏️write in front✏️
📝个人主页:陈丹宇jmu
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
🙉联系作者🙈by QQ:813942269🐧
🌈致亲爱的读者:很高兴你能看到我的文章,希望我的文章可以帮助到你,祝万事顺意🏳️🌈
✉️少年不惧岁月长,彼方尚有荣光在 🏆

⬜⬜⬜ ---🟧🟨🟩🟦🟪前言🟧🟨🟩🟦🟪---⬜⬜⬜
最小化最大算法构造决策树,并自底向上计算每个节点的minimax值,最终从根结点选择minimax值最大的分支,作为行动策略。
当一个零和博弈双方每一步可选动作数量较多时,决策树会变得非常庞大,因此构造决策树,并对其进行遍历,求取每个minimax值将会非常耗时。
在决策树的构建与搜索过程中,存在一些不必要搜索的节点。如果不展开不必要搜索的节点,将会极大的节省搜索时间。
本篇将讲解极小化极大算法的优化版本——AlphaBeta剪枝算法。
🚩本篇主要内容
Alpha-Beta剪枝算法
- Alpha-Beta算法的由来
- Alpha-Beta算法原理
- Alpha-Beta算法剪枝过程
- Alpha-Beta算法剪枝伪代码
📋笔记目录
🚩本篇主要内容
📒一. Alpha-Beta剪枝算法
⏳1.1. Alpha-Beta算法的由来
⏳1.2. Alpha-Beta算法原理
⏳1.3. Alpha-Beta算法剪枝过程
⏳1.4. Alpha-Beta算法剪枝伪代码
📒一. Alpha-Beta剪枝算法
⏳1.1. Alpha-Beta算法的由来
极小化极大算法在完全信息零和博弈中,基于己方努力使得在N步后优势最大化(即评估函数输出值最大化)和对方努力使得N步后己方优势最小化这两个出发点,构建决策树。在决策树上通过这两个出发点的内在逻辑进行搜索,最后给出行动策略。
显然,极小化极大算法需要展开整个决策树,对于局面复杂的问题,其搜索空间将会非常大。同时,我们可以清晰地看到有部分节点是否被搜索不会影响最后的结果,因此,无需展开此类节点以及计算此类节点的子节点的估值。
通过上述方法,可节省算法的搜索时间。这种不展开搜索不必要节点的算法,被称为——Alpha-Beta剪枝算法。
⏳1.2. Alpha-Beta算法原理
Alpha-Beta剪枝算法可加速极小化极大算法的搜索过程。在构建和搜索决策树时,每个节点除存储局面估值之外,还存储可能取值的上下界。下界即为Alpha值,上界即为Beta值。
⏳1.3. Alpha-Beta算法剪枝过程
Alpha Beta 剪枝算法的基本依据是:棋手不会做出对自己不利的选择。依据这个前提,如果一个节点明显是不利于自己的节点,那么就可以直接剪掉这个节点,AI会在MAX层选择最大节点,而玩家会在MIN层选择最小节点。那么如下两种情况就是分别对双方不利的选择:1.在MAX层,假设当前层已经搜索到一个最大值 X, 如果发现下一个节点的下一层(也就是MIN层)会产生一个比X还小的值,那么就直接剪掉此节点。也就是在MAX层的时候会把当前层已经搜索到的最大值X存起来,如果下一个节点的下一层会产生一个比X还小的值Y,那么之前说过玩家总是会选择最小值的。也就是说这个节点玩家的分数不会超过Y,那么这个节点显然没有必要进行计算了。
通俗点来讲就是,AI发现这一步是对玩家更有利的,那么当然不会走这一步。
1. 在MIN层,假设当前层已经搜索到一个最小值 Y, 如果发现下一个节点的下一层(也就是MIN层)会产生一个比Y还大的值,那么就直接剪掉此节点。
这个是一样的道理,如果玩家走了一步棋发现其实对AI更有利,玩家必定不会走这一步。
如图所示,在第二层,也就是MIN层,当计算到第三个节点的时候,已知前面有一个3和一个6,也就是最小值为3。 在计算第三个节点的时候,发现它的第一个孩子的结果是5,因为它的孩子是MAX节点,而MAX节点是会选择最大值的,那么此节点的值不会比5小,因此此节点的后序孩子就没有必要计算了,因为这个节点不可能小于5,而同一层已经有一个值为3的节点了。
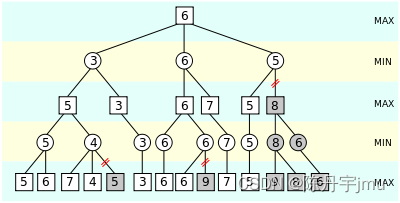
其实这个图里面第三层分数为7的节点也是不需要计算的。
这是 MAX 节点的剪枝,MIN节点的剪枝也是同样的道理。 Alpha-Beta 剪枝的 Alpha 和 Beta 分别指的是MAX 和 MIN节点。
⏳1.4. Alpha-Beta算法剪枝伪代码
function minimax(node, depth)
if node is a terminal node or depth = 0
return the heuristic value of node
if the adversary is to play at node
let α := +∞
foreach child of node
α := min(α, minimax(child, depth-1))
else {we are to play at node}
let α := -∞
foreach child of node
α := max(α, minimax(child, depth-1))
return α