| LeetCode刷题记录 |
文章目录
- LeetCode54.螺旋矩阵
- 思路
- 代码
- LeetCode59 螺旋矩阵Ⅱ
- 思路
- 代码
LeetCode54.螺旋矩阵
给你一个 m 行 n 列的矩阵
matrix,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例一
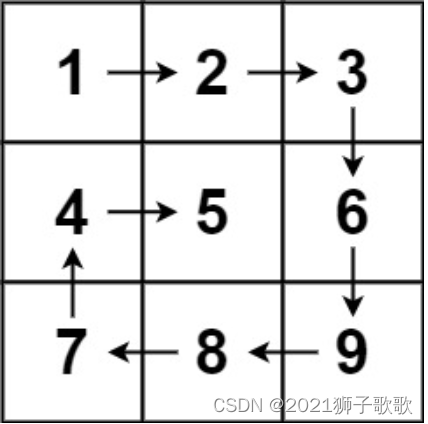
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例二
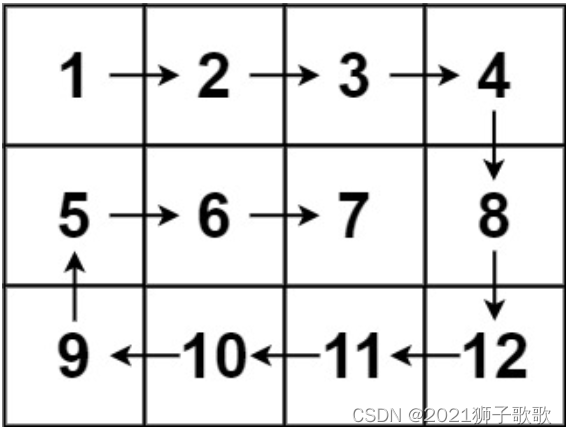
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]

思路
就是说,给我们一个二维数组,然后我们需要按顺时针的顺序遍历二维数组,然后把每一个遍历到的数据放到一个一维数组中,最后返回这个一维数组。
思路很简单,关键是怎么控制让他顺时针去访问,什么时候向下走
什么时候向左走,什么时候向右走 等问题
如图分析:

但是此时还会存在问题
因为此题给的是 m*n 的矩阵不一定是正方形
因为不是正方形,边界的长和宽本来就不相同,在顺时针遍历的时候,可能某一次遍历完,已经遍历完所有元素了,但是由于参数的原因还会继续向后走。
**解决方法:**因此我们每走完一步都要判断是不是已经走完了 m*n个元素,如果是,那么直接提前break即可。
如下图所示: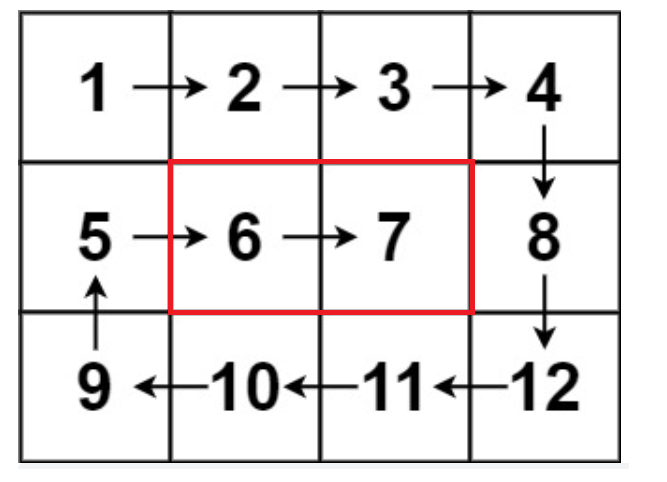
-
此时是第二轮从left->right的遍历,此时top=1,left=1,right=2,bottom=1
-
这一次遍历之后,top++,变成2,下一次right不变,从top->bottom
因为top>bottom 所以不会进入
-
然后right–,变成1,下一次bottom不变,right->left 。
-
right=1,left=1,会进入 right->left的循环 而此时所有的元素都已经放入了目标的一维数组,所以此时进入循环 就会重复访问。
但是此时 如果是正方形,right一定是小于left的,因为正方形的边界都相同,每一轮之后,边界都等大的缩小1,但是由于是长方形,可能本来长就大于宽,因此出现了这种情况
代码

LeetCode59 螺旋矩阵Ⅱ
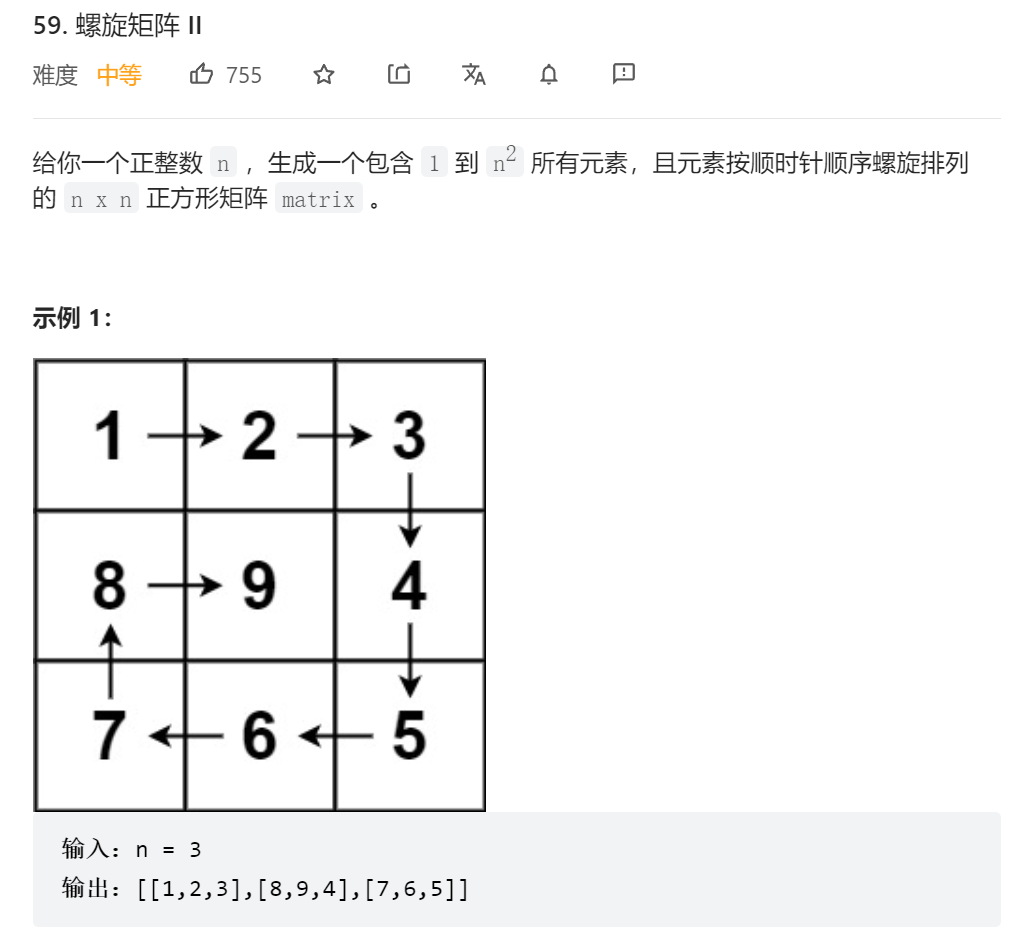
给你一个正整数 n ,生成一个包含 1 到
n^2所有元素,且元素按顺时针顺序螺旋排列的n x n正方形矩阵matrix。
示例一
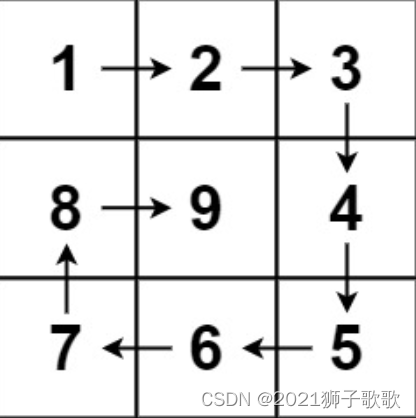
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例二
输入:n = 1
输出:[[1]]
思路
- 定义一个n*n的二维数组
- 从外层到内层,按照顺时针顺序依次把 从1到n^2的数放入数组
- 循环判断条件是 count<=n*n
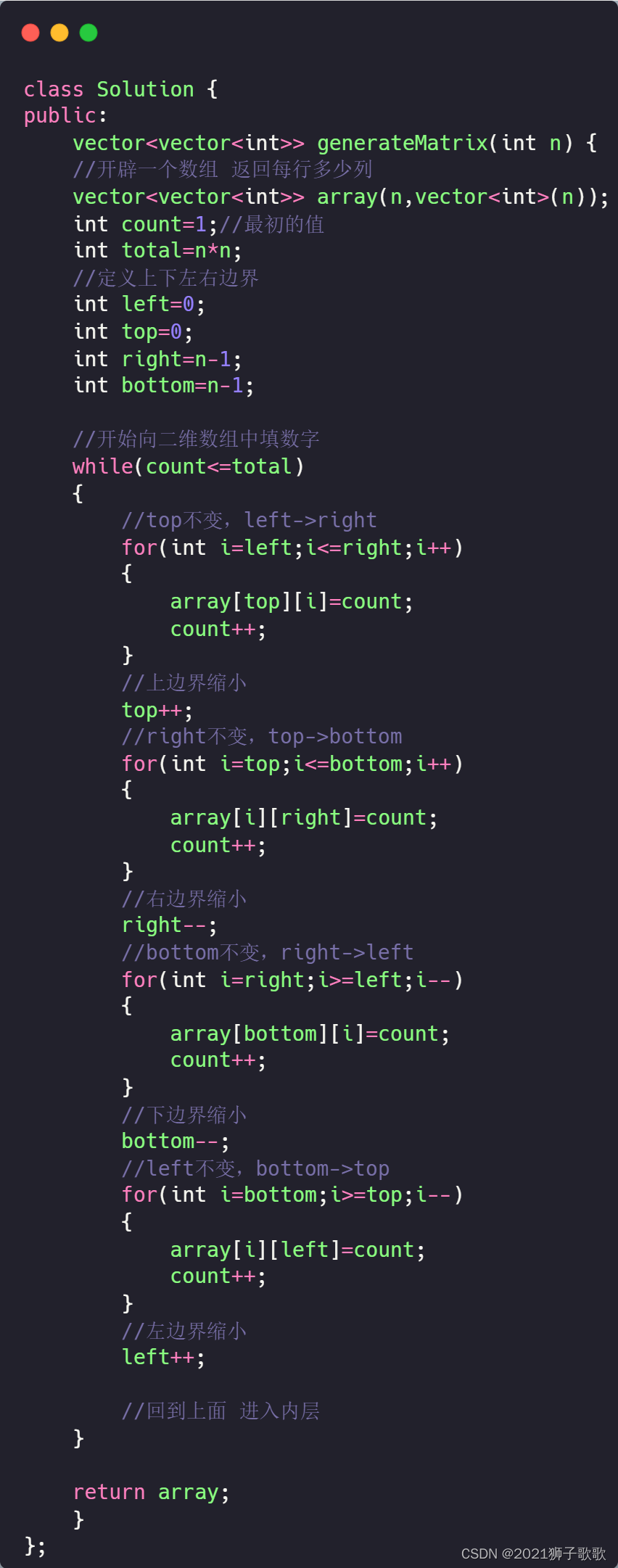
代码