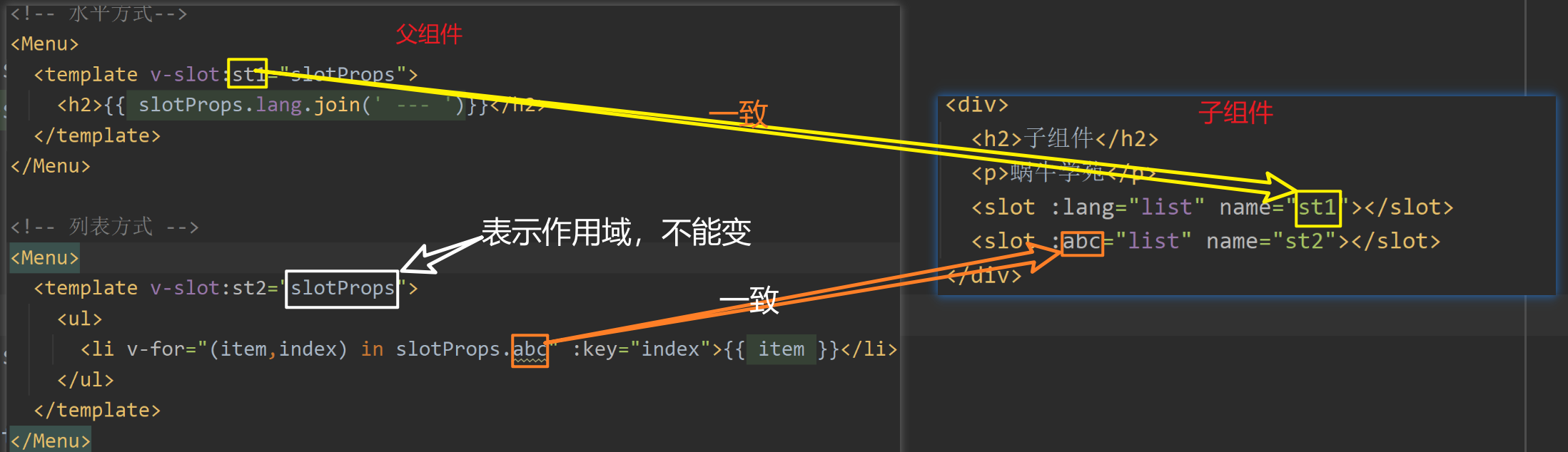
记录一下以前博客的证明过程，补充一下之前的结论

在算法导论中lgn一般指2为底的对数n，特此说明

---

以前写的博客记录了一下分治递归时间复杂度的结论，发现少了一个正则条件，而且也不覆盖所有的一般情况

https://blog.csdn.net/qq_19841133/article/details/103640028

考虑分支递归时间复杂度T(n)，有下面的更一般结论
T(n) = aT(n/b) + f(n)

像下面举了一个例子T(n)，计算发现f(n)较大，同时还要验证正则条件a(f(n/b)) <= cf(n)，就是图片The regularity condition部分

为什么要正则条件?

在递归式T(n) = aT(n/b) + f(n)中

首先, f(n) 可以直观的被解释为把一个规模为n的问题分解成a个规模为n/b的子问题和合并a个子问题的解的代价

其次，af(n/b) 可以被解释为把a个规模为n/b的子问题分解成$a^2$个规模为$n/b^2$ 的子问题和合并$a^2$个子问题解的代价。

那么，条件 af(n/b) ≤ cf(n), for c < 1 和足够大的 n, 可以被解释为上述第一点f(n)合并的代价是上述第二点af(n/b)代价的准确界。

则当一个问题被分解成越来越小的子问题，分解和合并的代价变得越来越小。

---

例子1
$T(n)=5T(n/2)+n^2$
这个比较简单，直接套$d<lo{g}_{b}a$，$T(n)=n^{lo{g}_{2}5}$

---

例子2
$T(n)=27T(n/3)+n^{3}lgn$
对应(2)公式
$T(n)=(n^{3}l{g}^{2}n)$

---

例子3
$T(n)=2T(n/2)+n/lgn$
a=2,b=2,f(n)=n/lgn
这里对应(2)公式，但是发现k=-1，不满足k>=0，因此不用主定理法求解

---

例子4
改变变量法

有时代数操作可以把一个未知的递归式转换成已知可解的递归式

如下Tn，这里b表示不出来，不能用主定理法，但是我们可以替换一下变量
$T(n)=2T(\sqrt{n})+lgn$

令$m=lgn$, 则 $n=2^m$

代回Tn
$T(2^m)=2T(2^{m/2})+m$

令$S(m)=T(2^m)$得出新的递归式
S(m) = 2S(m/2) + m

用主定理法解得，$d=lo{g}_{b}a$，S(m) = mlgm

用m代回
$S(m)=T(2^m)=T(n)=mlgm=lgnlglgn$

---

主定理法证明，下面是主定理法一种特殊形式的证明，更一般的情况请查阅《算法导论》

$T(n)=aT(n/b)+c{n}^k$

将T(n)递归展开，假设展开了m层变成一个没有递归的完整的求和序列

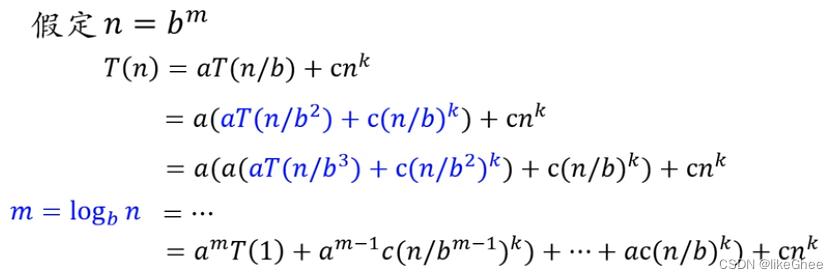
令T(1) = c，写成求和公式形式

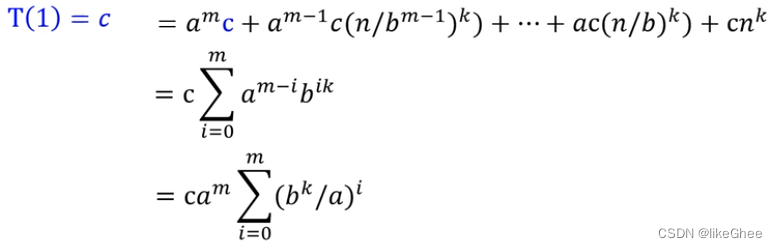
那么解决求和部分${\sum }_{i=0}^m(b^k/a{)}^i$即可，其实就是等比数列求和，分类讨论三种情况

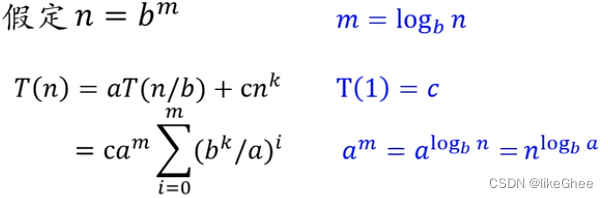
等比数列求和r分成大于0等于0小于0情况

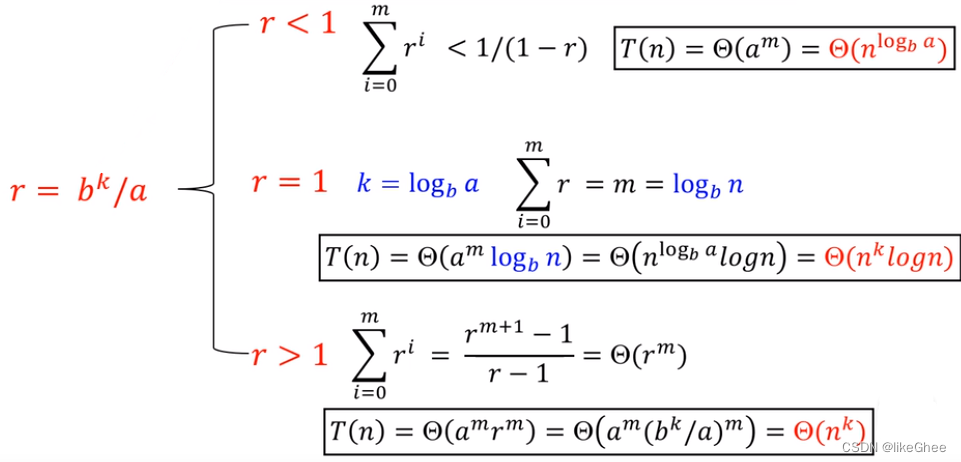
最后结论为

---

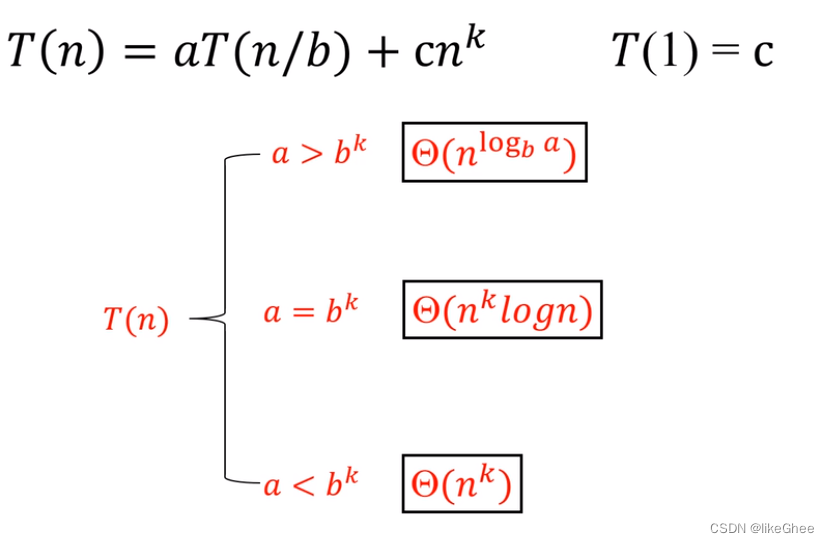
更一般的情况证明在《算法导论》中，数学分析难度了已经，先放一放先（）