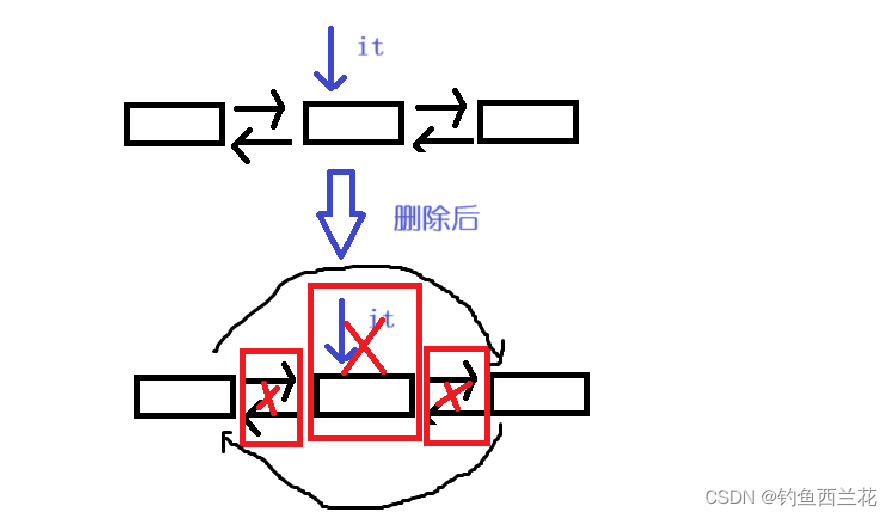
(1)辗转相除法求最大公约数(gcd)
辗转相除法, 又名欧几里德算法(Euclidean algorithm),是求最大公约数的一种方法。它的具体做法是:用较小数除较大数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。原理也很简单:设gcd(a,b)表示a与b的最大公约数(a>b),则满足gcd(a,b)=gcd(b,b%a)。以下就是算法步骤:
| a | b |
| 72 | 48 |
| 48 | 24 |
| 24 | 0 |
| 根据这张表我们可以知道当b=0的时候,左边的24就是a,b的最大公约数。在每一次迭代中(设a为较大数,b为较小数),a为上一轮的b,b=a%b,所以这个函数用递归实现就是 |
int gcd(int a,int b)
{
return b==0?a:gcd(b,a%b);
}
这是三元运算符(? : )D=a?b:c的意思是先判断条件a。如果a为true,就把b的值赋给D;如果如果a为false,就把c的值赋给D。运用到欧几里得法就是:先判断较小数b是否为0,如果是的话直接返回a;如果不是的话就把b作为较大数,a%b作为较小数传入下一个递归。实现的过程中记住int gcd(int a,int b)中a为较大数,b为较小数就可以了。
(2)拓展欧几里得算法
我们先介绍一下贝祖定理:即如果a、b是整数,那么一定存在整数x、y使得ax+by=gcd(a,b)。拓展欧几里得算法就是把x,y的值计算出来。
当到达递归边界的时候,b==0,a=gcd(a,b) 这时可以观察出来这个式子的一个解:a*1+b * 0=gcd(a,b),x=1,y=0,注意这时的a和b已经不是最开始的那个a和b了,所以我们如果想要求出解x和y,就要回到最开始的模样。因为递归的相邻两层的参数a,b都是满足辗转相除法状态转移方法的,所以我们可以按照公式一层一层计算上去。状态转移公式推导如下:
这个代码用递归可以实现,代码如下
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
int x,y;
void solution(int a,int b)
{
if(b==0)
{
x=1;
y=0;//递归到了底部,很明显x=1,y=0是一个解
}
else
{
solution(b,a%b);
int temp=y;
y=x-(a/b)*y;
x=temp;//递归到了底部以后开始回溯,根据每一层的参是一层一层往上计算
}
}
int main()
{
while(1==1)
{
int a,b ;
cin>>a>>b;
cout<<"要解决的方程是: " <<a<<"x+"<<b<<"y=gcd("<<a<<","<<b<<")\n";
solution(a,b);
cout<<"方程解为: x="<<x<<" y="<<y<<"\n";
}
return 0;
}
这段代码主要有两个部分组成:
①递归先到底部以后先找出一组原始解:x=1,y=0,并终止递归,中止递归的条件就是b=0。对应代码部分是:
if(b==0)
{
x=1;
y=0;//递归到了底部,很明显x=1,y=0是一个解
}
②因为方程解x,y的交换操作是在递归调用之后,所要采用的递归写法就是线性递归(非尾递归)的写法。就是调用拓展欧几里得函数以后再按照公式根据下一层递归传来的x,y和自身的参数a,b来执行x,y的转换操作。
线性递归:下一个函数结束以后此函数还有后续,所以必须保存本身的环境以供处理返回值。
代码如下:
else
{
solution(b,a%b);
int temp=y;
y=x-(a/b)*y;
x=temp;//根据每一层的参数是一层一层往上计算
}
这个过程的运行结果如下图所示(以a=72,b=48为例子):
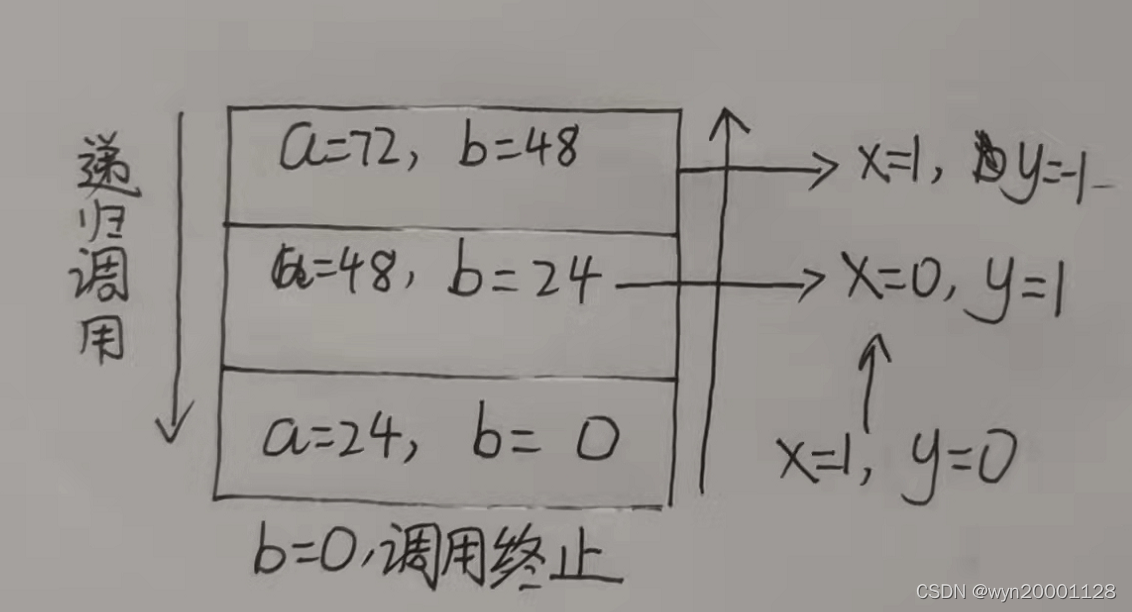
运行结果如下:

(3)分解质因数
质数:如果一个数的约数只有1和它本身那么这个数就是质数。且质数这个概念是专门针对大于2的自然数的。
合数:自然数当中除了合数剩下的数就是质数。
每一个自然数都满足一个唯一分解定理:每个大于1的自然数,要么本身就是质数,要么可以写为2个或以上的质数的积,而且这些质因子按大小排列之后,写法仅有一种方式。公式如下:
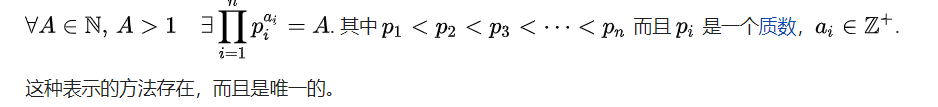
根据这个定理可以编程实现质因数的分解,以下为代码和代码的解释:(以24为例)
遍历质因数:先写一个i是从2到24的循环,判断i是否可以被24整除。当判断出i可以整除24的时候,就彻底去除这个因子。例如24可以分解为3*2的三次方,所以24要除以2三次。依次类推就可以实现功能。最后要分解的合数就一定可以分解成唯一分解定理分解的形式。
附:要注意循环的次数为:
for(i=2;i<=n;i++)
因为这个算法是每一次迭代解出一个质因子和对应的次数,所以2到n都有可能是,所以要写一个从2到n的循环(代码优化思路就是大于sqrt(n)的质因数有且只有一个,且次数一定为1)。下面是完整代码:
#include <iostream>
#include <vector>
using namespace std;
int main ()
{
int input,i,j;
vector <int> prime_factor;
vector <int> power;
while(1==1)
{
cout<<"请输入你要分解的数:";
cin>>input;
int n=input;
for(i=2;i<=n;i++)
{
if(input%i==0)//判断是否可以被整除
{
prime_factor.push_back(i);
int num=0;
while(input%i==0)//计算出质因子的个数并且把质因子从里面剔除掉
{
num++;
input/=i;
}
power.push_back(num);
}
}
cout<<"这个数可以分解为:"<<"\n" ;
for(i=0;i<=power.size()-1;i++)
{
if(i==power.size()-1)
{
for(j=1;j<=power[i];j++)
{
if(j==power[i]) cout<<prime_factor[i]<<"\n\n";
else cout<<prime_factor[i]<<"*";
}
}
else
{
for(j=1;j<=power[i];j++)
cout<<prime_factor[i]<<"*";
}
}
prime_factor.clear();
power.clear();
}
return 0;
}
}
代码的执行结果为:

(4)埃氏筛素数法(枚举n以内的素数)
首先将2到n范围内的整数写下来,其中2是最小的素数。将表中所有的2的倍数划去,表中剩下的最小的数字就是3,他不能被更小的数整除,所以3是素数。再将表中所有的3的倍数划去……以此类推。代码逻辑就是每一次找到一个素数的时候就把所有该素数的倍数删掉就可以了。核心思想就是:从2开始,将每个质数的倍数都标记成合数,以达到筛选素数的目的。
埃氏筛素数法的目的就是把所有的1到n内所有满足某个性质的素数倍数除掉。这些素数可以看作一个素数集合X,其中X满足:x属于X,2*x<=n。代码如下:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main ()
{
int i,j;
while(1==1)
{
cout<<"请输入您所查询的数的范围:";
vector<bool> array(1000000,false);
cin>>j;
for(i=2;i<=j/i;i++)
{
if(array[i-1]==false)
{
int temp=i+i;
while(temp<=j)
{
array[temp-1]=true;
temp+=i;
}
}
}
cout<<j<<"以内的质数为:";
for(i=0;i<=j-1;i++)
{
if (array[i]==false)
cout<<i+1<<" ";
}
cout<<"\n\n";
}
return 0;
}
运行结果如下:

(5)线性筛素数法
在用埃式筛法的同时,同一个数字也许会被筛选多次,比如6先被2筛选一次,再被3筛选一次,这样就浪费了很多不必要的时间。欧拉筛法就是在埃氏筛法的基础上,让每个合数只被它的最小质因子筛选一次,以达到不重复的目的。比如说20如果使用埃式筛法会被2和5同时筛掉
这种算法实现的具体步骤就是:(以n=100为例)
(1)写一个从2到100的循环,因为这个算法再执行的过程中要记录下质数,这样就可以把2到100的所有质数保存出来。
(2)对于循环中的任意一个数i,执行以下两个步骤
(①)判定i是否为质数,如果是质数的话把它保存下来。
(②)枚举所有比i小的质数组成一个集合X,标记i * j为合数,j属于X。但是一旦出现i mod j==0,就break。(这是关键,可以实现每一个数都被最小质因子筛掉。一旦出现i mod j1=0,那么i * D ( D为大于j1的质数)的最小质因子就是j1。但是如果不加这个限制继续标记i * j2,那么i * j2的最小质因子是j1却被j2标记,就不满足算法的核心要求了。)
以8为例,首先标记82=16,但是如果没有这个条件,下一个标记83=24,但是显然24的最小质因子是2,所以24不是被它的最小质因子筛选掉的。上述算法的具体代码实现如下:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main ()
{
while(1==1)
{
vector <int> prime;
int N,i,j;
cout<<"请输入您所要查询的数:" ;
cin>>N;
vector <bool> record;
for(i=1;i<=N;i++) record.push_back(false);//记录哪个数是否被标记
for(i=2;i<=N;i++)
{
if(record[i-1]==false) prime.push_back(i);
for(j=0;j<prime.size()&&i*prime[j]<=N;j++)
{
int A=i*prime[j];
record[A-1]=true;
}
}
cout<<N<<"以内的质数为:";
for(i=0;i<prime.size();i++) cout<<prime[i]<<" ";
cout<<"\n\n";
prime.clear();
record.clear();
}
return 0;
}
(6)欧拉函数(小于N且和N互质的正整数的个数)
就是对于一个正整数N,小于N且和N互质的正整数(包括1)的个数。记作φ(n) 。φ(N) 的表达式如下所示:
设
n
=
p
1
k
1
∗
p
1
k
2
∗
p
1
k
2
∗
.
.
.
.
p
n
k
n
,
p
i
是质数,
k
i
是对应的指数
φ
(
n
)
=
n
∗
(
1
−
1
p
1
)
∗
(
1
−
1
p
2
)
∗
.
.
.
.
.
.
(
1
−
1
p
n
)
设n=p1^{k1}*p1^{k2}*p1^{k2}*....pn^{kn},p_i是质数,k_i是对应的指数\\\\φ(n)=n*(1-\frac {1} {p1})*(1-\frac {1} {p2})*......(1-\frac {1} {pn})
设n=p1k1∗p1k2∗p1k2∗....pnkn,pi是质数,ki是对应的指数φ(n)=n∗(1−p11)∗(1−p21)∗......(1−pn1)
具体的实现方法就是对一个数进行质因数的分解。如果查出一个质因子,先把这个质因子消除干净,然后进行下列公式的迭代:
r
e
s
u
l
t
=
r
e
s
u
l
t
∗
(
1
−
1
p
n
)
r
e
s
u
l
t
初值为
N
result=result*(1-\frac {1} {pn}) \quad result初值为N
result=result∗(1−pn1)result初值为N
代码如下:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main ()
{
while(1==1)
{
int N,i;
cout<<"请输入你想要查询的欧拉函数值:";
cin>>N;
int result=N;
int target=N;
while(N>1)
{
for(i=2;i<target;i++)
{
if(N%i==0)
{
while(N%i==0) N=N/i;
result=result*(i-1)/i;
}
}
}
cout<<result<<"\n\n";
}
return 0;
}
(7)快速幂算法
所谓的快速幂,实际上是快速幂取模的缩写,简单的说,就是快速的求一个幂式的模(余)。在程序设计过程中,经常要去求一些大数对于某个数的余数,为了得到更快、计算范围更大的算法,产生了快速幂取模算法。
这个算法是基于以下式子来编程的算法:
(
1
)
a
2
n
m
o
d
c
=
(
a
2
n
−
1
m
o
d
c
)
∗
(
a
2
n
−
1
m
o
d
c
)
m
o
d
c
(
2
)
a
10
=
a
(
1010
)
2
=
a
2
3
∗
a
2
1
(
3
)
(
∏
i
=
1
n
−
1
X
i
m
o
d
c
)
∗
(
X
n
m
o
d
c
)
=
(
∏
i
=
1
n
X
i
m
o
d
c
)
(
2
)
,
(
3
)
公式就是快速幂算法的实现思路。具体思路就是把原始
式子
a
X
分解成(
2
)这样的形式且(
3
)公式是从第一个形如
a
2
n
的因子开始进行迭代,最终可以计算出结果。
(1)\;a^{2^{n}}\;mod \;c=\;(a^{2^{n-1}}\;mod\;c)*(a^{2^{n-1}}\;mod\;c)\;mod\;c\\(2)\;a^{10}=a^{(1010)_2}=a^{2^{3}}*a^{2^{1}}\\(3)(\prod_{i=1}^{n-1}X_i\;mod\;c)\;*(X_n\;mod\;c)=(\prod_{i=1}^{n}X_i\;mod\;c)\\(2),(3)公式就是快速幂算法的实现思路。具体思路就是把原始\\式子a^{X}分解成(2)这样的形式且(3)公式是从第一个形如a^{2^{n}}\\的因子开始进行迭代,最终可以计算出结果。
(1)a2nmodc=(a2n−1modc)∗(a2n−1modc)modc(2)a10=a(1010)2=a23∗a21(3)(∏i=1n−1Ximodc)∗(Xnmodc)=(∏i=1nXimodc)(2),(3)公式就是快速幂算法的实现思路。具体思路就是把原始式子aX分解成(2)这样的形式且(3)公式是从第一个形如a2n的因子开始进行迭代,最终可以计算出结果。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main ()
{
while(1==1)
{
int A,B,C;
cout<<"请依次输入3个数:";
cin>>A>>B>>C;
cout<<"您要计算"<<A<<"的"<<B<<"次方除以"<<C<<"的余数:\n" ;
int result=1;
int record=A%C;
while(B)
{
if(B&1==1) result=(result*x)%C;
B>>=1;
record=record*record%C;//迭代更新record,可见公式1
}
cout<<result<<"\n\n";
}
return 0;
}
代码的解释:方法就是从B(2进制)从最低位到最高位进行遍历来找到所有是1的位数,从而来把A的B次方化成公式(2)的形式。并且设置了record变量是为了记录每一个 A2n%C 的值来辅助计算。一直到B为0位置(因为此时已经遍历了B的所有位数)
(8)容斥原理
容斥原理是一种重要的组合数学方法,这种方法可以求解任意几个集合的并集,或者求复合事件的概率。我们要先将所有单个集合的大小计算出来,然后减去所有两个集合相交的部分,再加回所有三个集合相交的部分,再减去所有四个集合相交的部分,依此类推,一直计算到所有集合相交的部分数学公式表达如下:具体代码实现自己想办法,不过大概可以通过2进制来记录集合是否被使用过。
集合
X
=
[
X
1
,
X
2
,
X
3
.
.
.
.
.
.
X
n
]
,
则
X
1
,
X
2
,
X
3
.
.
.
.
.
.
X
n
的并集
S
为:
S
=
∑
奇数
(
X
i
∩
X
j
∩
.
.
.
)
−
∑
偶数
(
X
k
∩
X
b
∩
.
.
.
)
\;集合X=[X_1,X_2,X_3......X_n],则X_1,X_2,X_3......X_n的并集S为:\\S=\sum_{奇数}(X_i\cap X_j \cap...)-\sum_{偶数}(X_k\cap X_b \cap...)
集合X=[X1,X2,X3......Xn],则X1,X2,X3......Xn的并集S为:S=∑奇数(Xi∩Xj∩...)−∑偶数(Xk∩Xb∩...)
(9)高斯消元法
高斯消元法是求解线性方阵组的一种算法,它也可用来求矩阵的秩,以及求可逆方阵的逆矩阵。它通过逐步消除未知数来将原始线性系统转化为另一个更简单的等价的系统。它的实质是通过初等行变化,将线性方程组的增广矩阵转化为行阶梯矩阵,原理是矩阵进行初等行变换的时候解是不变的。下面是算法的过程:
(1)已知方程组
x
+
y
+
z
=
3
2
x
+
y
−
z
=
2
3
x
−
y
−
z
=
1
x+y+z=3\\2x+y-z=2\\ 3x-y-z=1\\
x+y+z=32x+y−z=23x−y−z=1
(2)根据方程式构造增广矩阵
∣
1
1
1
3
2
1
−
1
2
3
−
1
−
1
1
∣
\begin{vmatrix} 1 & 1 & 1 &3\\ 2 & 1 & -1 &2\\ 3 & -1 & -1 &1\\ \end{vmatrix}
12311−11−1−1321
(3)把增广矩阵的系数矩阵构建成上三角矩阵,具体方法就是:枚举系数矩阵每一列,对于第i列,先将第i行和第i行以下所有行中第i个数绝对值最大的行换到最顶端。(此时这个数为第一个非零元),而后把这个数化为1。通过第三类初等行变换(如下图公式),用当前行将下面所有的列消成0。
c
j
=
c
j
+
d
∗
c
i
(
c
i
为第
i
行,
c
j
为第
j
行,
j
>
i
)
c_j=c_j+d*c_i(c_i为第i行,c_j为第j行,j>i)
cj=cj+d∗ci(ci为第i行,cj为第j行,j>i)
最终可以化为以下形式:
∣
1
−
1
3
−
1
3
1
3
0
1
−
1
5
4
5
0
0
8
3
8
3
∣
\begin{vmatrix} 1 & \ - \frac{1}{3} & - \frac{1}{3} & \frac{1}{3}\\ 0 & 1 & - \frac{1}{5} &\frac{4}{5}\\ 0 & 0& \frac{8}{3}&\frac{8}{3}\\ \end{vmatrix}
100 −3110−31−5138315438
枚举完所有列,化简到这一步以后,存在三种情况:
①系数矩阵刚好可以化为一个完美的上三角矩阵,也就是不存在零行(一行全部都是0),说明只有一个解,增广矩阵往上推就可以推出所有解。
②若存在零行且对应系数的增广系数为0,则代表方差组存在无数个解。
③若存在零行且对应系数的增广系数不为0,则代表方程组无解。
具体代码思路如下:
1 根据方程式构造增广矩阵。
2 写一个循环枚举系数矩阵的所有列,并执行对应行变换把枚举系数矩阵化为上三角,并且同时要设置一个record记录目前非零行的个数。
3 使用record和n的关系判断最终结果,可以的话可以求出最后的解。代码如下:
(10)组合数
(1)杨辉三角:
1
1
2
1
1
3
3
1
1
4
6
4
1
很明显第
n
行的数为:
C
n
0
,
C
n
1
,
C
n
2
.
.
.
,
C
n
n
−
1
,
C
n
n
且存在递推关系
C
n
i
=
C
n
−
1
i
+
C
n
−
1
i
−
1
例如第三行的第二个数是
3
,恰好等于第二行的第一个数
1
加上
第二行的第二个数
2
1\\ 1\:2\:1\\ 1\:3\:3\:1\\ 1\:4\:6\:4\:1\\ 很明显第n行的数为:C_n^0,C_n^1,C_n^2...,C_n^{n-1},C_n^n\\且存在递推关系C_n^i=C_{n-1}^i+C_{n-1}^{i-1}\\例如第三行的第二个数是3,恰好等于第二行的第一个数1加上\\第二行的第二个数2
1121133114641很明显第n行的数为:Cn0,Cn1,Cn2...,Cnn−1,Cnn且存在递推关系Cni=Cn−1i+Cn−1i−1例如第三行的第二个数是3,恰好等于第二行的第一个数1加上第二行的第二个数2
(2)卡特兰数问题(此问题解法太经典,看图可知)
给定 n 个 0 和 n 个 1,它们将按照某种顺序排成长度为 2n 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

(11) 质数的判定(朴素法)
质数的定义就是:公因数只有1和它本身的数,因此要判定一个数N是否为质数,只需判定在区间[2,i]之间不存在N的约数就行(i为N开平方根之后的数)
bool check (int n)
{
int i;
bool flag=true;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
flag=false;
}
return flag;
}