囚徒困境大家应该都比较熟悉了，我觉得这篇的意义大概在与，经济学术语的运用？

囚徒困境：个人理性与集体理性的矛盾

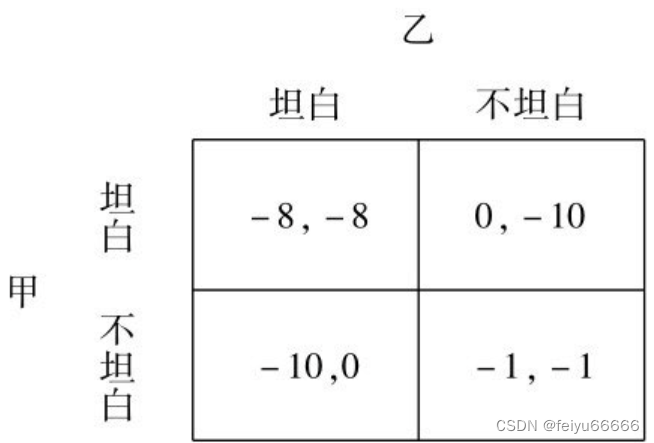
假定有两个犯罪嫌疑人共同作案。警察抓住他们以后，分开拘押，并告诉他们：可以选择坦白，或是不坦白；如果一个人坦白，而另一个人不坦白，则坦白的一方会被立即释放，而不坦白的一方被判10年；如果两人都坦白，则会每人各判8年；如果两人都抵赖，因证据不足，则每人在关押1年后释放。那么，这两个犯罪嫌疑人该如何选择呢？

我们看到，这个博弈有两个参与人：犯罪嫌疑人（囚徒）甲和乙；每个人有两个行动：坦白或不坦白；两个人隔离审查，谁都不能观察到对方坦白还是不坦白，因此是一个不完美信息静态博弈。由于不能观察到对方的行动，也就没有办法把自己的选择建立在对方行动的基础上，因而，战略和行动是一回事（在静态博弈中，行动和战略可以交换使用）。这个博弈的支付结构如下图所示，图中列代表囚徒甲，行代表囚徒乙，甲的选择在第一列，乙的选择在第一行；矩阵中方框里的两个数字，第一个数字为甲的支付，第二个数字为乙的支付。这种描述博弈的方式我们叫标准式（normal form）。

现在我们来看参与人甲和乙会如何决策。我们假设参与人是理性的，不想坐牢，哪怕是多坐一天也会带来更多的痛苦，因此，他的目标就是能少坐就少坐；我们还假定每个人只关心自己，不关心对方（如果两个囚徒是父子关系或兄弟关系，他们的行为也许会与我们这里的情况不同）。我们先考虑甲的选择，他面对的问题是：如果乙坦白的话，自己坦白判8年，不坦白判10年，那么坦白比不坦白好；如果乙不坦白，自己坦白会被立即释放，不坦白则判1年，坦白还是比不坦白好。因此，对于甲来说，不管对方坦白不坦白，自己的最优选择都是坦白。同样，对乙来说也是一样的。所以，每一个人的最优选择都是坦白。

一般来说，博弈中每个参与人的最优选择依赖于别人的选择，但在上述囚徒困境博弈中，每个人的最优选择与他人的选择无关。这种独立于他人选择的最优战略称为该参与人的占优战略（dominant strategy）。正式地，所谓“占优战略”是指在博弈中参与人的某一个战略，不管对方使用什么战略，只要参与人使用这一战略，都可以给自己带来最大的支付。或者说，参与人的这一战略在任何情况下都优于自己的其他战略。占优战略类似我们常说的“上策”或“上上策”，如“三十六计，走为上策”。在博弈中，如果每一个参与人都有一个占优战略，则他们显然都会选择这一战略，那么，由占优战略组成的战略组合就构成了博弈的占优战略均衡（dominance equilibrium）。

显然在囚徒困境博弈中，坦白是每个参与人的占优战略。两个人都选择坦白也成了这个博弈的占优战略均衡。结果就是两个人都会坦白，各判8年。

但是，就两个囚徒而言，这个博弈中的帕累托最优是“都不坦白”，各坐1年牢。这就是我们讲的个人理性与集体理性的矛盾。尽管对两个人来讲，不坦白是最好的，但是每个人都会选择对自己最优的行动——坦白。结果对两个人都不好。这就回到我们前边讲的，个人理性不一定达到帕累托最优。

对此，我们可以用上一章中提到的“外部性”概念来解释。外部性可以简单理解为一个人的行为给别人所带来的影响。给定甲坦白，乙从不坦白（判10年）到坦白（判8年），可以让自己的刑期减少两年；但同时让甲的刑期从0年增加到了8年。这样，乙的行为不仅给自己带来了好处，还给甲带来了坏处。即乙的行为对甲来说有外部性，而且是不好的外部性，经济学中称为负外部性（negative externality）。类似地，甲的行为也会对乙产生负外部性。我们前面假定，人是理性的，他的目标是个人利益的最大化，而非集体利益的最大化，所以在存在负外部性的情况下，他出于追求自身的利益最大化选择的行动就不可能满足集体利益的最大化。这就导致个人选择和集体理性的矛盾。

囚徒困境又被称为“合作悖论”或“集体行动悖论”，即尽管合作能够给双方带来好处，但双方仍然是不合作。选择不合作是基于个体理性，而选择合作则是基于集体理性。

囚徒困境举例

这种个人理性与集体理性冲突的例子在生活中有很多。比如小孩子的学习负担问题，现在的孩子除了周一到周五的正常上课学习外，还要在周末去学习奥数、英语等等。其实这也是一个囚徒困境。我们可以设想一下，如果所有的学生周末都休息，考上重点中学和重点大学的一定是那些最聪明的孩子。问题是如果你周末休息，别的孩子周末补功课，那么可能别人考上了，你虽然聪明也可能考不上，所以你的最优选择也是周末补功课。结果是，所有的孩子一周7天都在学功课，最后考上重点中学和重点大学的仍然是那些聪明的孩子。竞争带来这种不合理的结果：每个人都忙活，但是最后的结果不一定对大家都好。我国现在的中小学生的学习强度这么高，从社会的角度讲肯定不是最优的。

企业之间的竞争也是一个囚徒困境。2000年6月9日，中国的九家彩电企业在深圳开会，制定了一些彩电型号的最低限价，形成价格同盟。但是，会议过去刚刚三天，6月12日，参加会议的一些企业就在南京等地率先降价，使得价格同盟名存实亡。一般来说，这种结盟是很难维持的。因为，给定你不降价，我先降价，就可以扩大销量，占领更多的市场份额。

类似地，企业做广告也可能是一个囚徒困境。做广告成本很高，不一定能给企业带来利润，但为什么大部分企业都做广告呢？假如某个行业有两个企业，如果每个企业都不做广告，各得10单位的利润；如果都做广告，各得4单位的利润；如果一个企业做广告，另一个企业不做广告，做广告的企业就可以赚到12，不做广告的企业只能赚到2。这个博弈的占优均衡，就是两个企业都做广告。因为无论别人做广告与否，你的最优选择都是做广告，最终两个企业的利润都变低了。即便两个企业事前达成一个协议，规定谁都不做广告，这个协议也不会得到遵守。

国与国之间的军备竞赛也与此类似。如果约定每个国家都不发展军备，将资源用于民用产品，对每个国家的国民都更好。但是，给定对方不生产武器，己方生产武器就可以取得军事上的优势；反之，如果对方发展军备，自己不发展的话，就会受到更大的威胁。所以，大家就会都搞军备竞赛。

公共产品（public goods）的供给也存在囚徒困境问题。所谓公共产品是指像国防、道路、桥梁等消费起来不会排斥他人的物品或服务。和公共产品相对应的概念是私人物品（private goods），如食物、衣服、汽车等消费起来具有排他性的物品或服务。一个苹果，若被我吃了，你就吃不到了。这就是消费的排他性。国防、道路、桥梁等公共物品，我消费时，你也可以消费，因此，这些物品没有消费的排他性。但正是这种消费的非排他性，使得个人没有积极性来提供这种产品，每个人都想着别人来提供，自己搭便车（free-riding）。这使得公共产品如果单靠私人来提供的话，会不足，从而使得整个社会的效用下降。因此，对于一个社会来说，如何有效地提供公共产品是公共治理的核心问题。

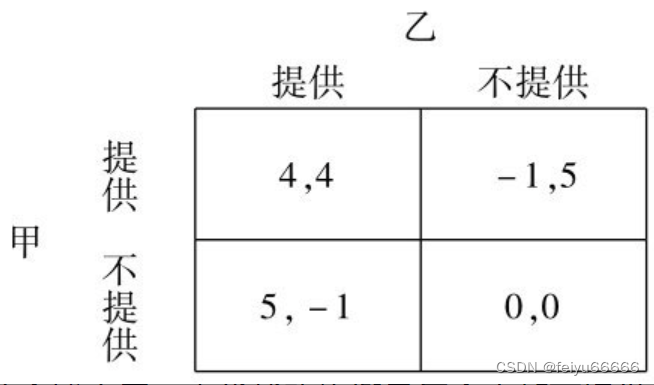
鉴于公共产品的重要性，下面，我们用修路的例子具体分析一下公共产品的提供问题。假如在一个由甲、乙两个人组成的社会中要修一条路。甲、乙二人都可以选择出力或不出力。如果两个人都出力，可以修好路，则每个人得到4个单位的收益；如果两个人都不出力，则修不成路，每个人得到的收益为零。如果一个人出力，另一个人不出力，则出力的人得不偿失，我们记为-1，不出力的人的收益为5。这样，我们就可以用下图表示公共产品博弈：

在这个博弈里，占优战略均衡是每个人都不提供。即，不论别人提不提供，己方都不提供。由此我们可以预测，在个人自愿基础上的均衡意味着没有公共产品的提供。所以，公共产品的提供一般需要政府使用强制的办法让个人为公共产品提供相应的服务或资金，例如，在现代社会中我们每个人都要交个人所得税，而在古代社会则是很多人都需要服劳役以及兵役等。

囚徒困境的一般形式

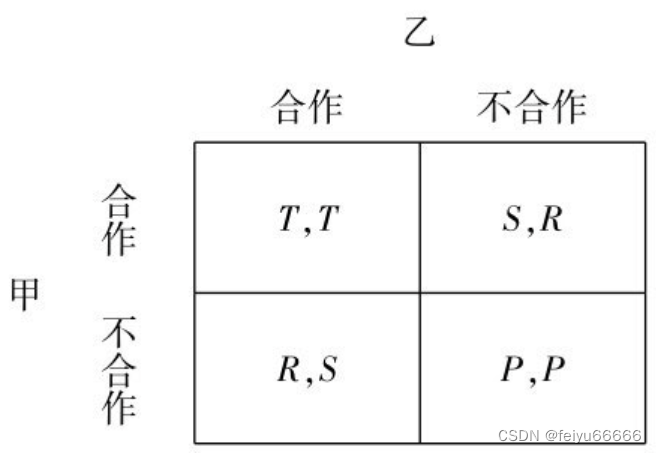
以上是几个具体的例子。下面我们给出囚徒困境博弈的一般形式。下图是一个二人博弈的支付矩阵。

博弈的双方都有两个选择：合作和不合作。如果两个人都选择合作，各自得到的支付为T；如果一个人合作另一个人不合作，合作方的支付为S，不合作方的支付为R；如果两个人都不合作，每一方的支付为P。

要使上述博弈成为一个囚徒困境需要满足这样一个条件：R＞T＞P＞S。即：对每个人来说，最好的结果是别人合作自己不合作（R），其次是两人都合作（T），再次是两人都不合作（P），最坏的结果是自己合作别人不合作（S）。另外，我们假定T+T＞R+S，即两人合作的总收益大于一人合作、另一人不合作时的总收益。只要满足这两个条件，无论支付的具体数字如何，结果一定是个人理性选择不满足集体理性。

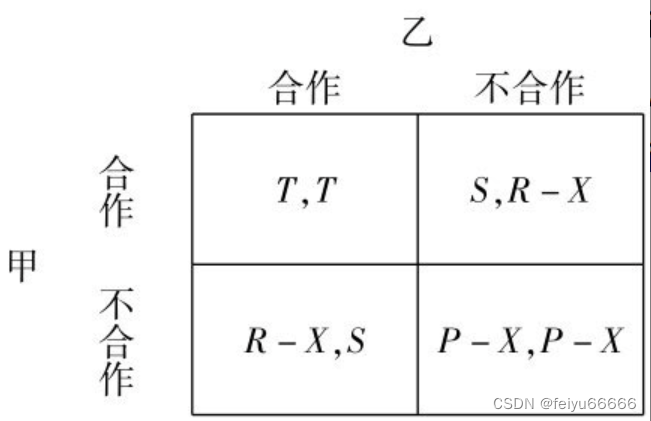
囚徒困境是社会合作面临的最大难题。古今中外，人类社会的许多制度安排（包括法律和社会规范）都是为解决囚徒困境而设计的。前面提到公共财政是解决公共产品供给中的囚徒困境问题，后面我们还会讲到所有权如何解决囚徒困境问题。现在考虑如何借助法律执行的当事人之间的合同解决交易中的囚徒困境。设想甲、乙两人在采取行动之前签订一个合同，合同规定：不合作的一方将受到处罚，罚金为X。再假定双方都相信这个合同能够在法律上得到有效执行。我们得到了下图。

此时，给定对方合作，己方如果也合作，则双方都得到T；己方如果不合作，对方如图2-3所示得到的支付为S，而己方得到的支付为R-X。显然，只要罚金X足够大，使得R-X＜T，那么，每个人的最好选择都是“合作”，双方都选择合作就成为一个均衡，解决了个人理性与集体理性的矛盾。这就是合同的价值。当然，如果当事人不相信合同能够得到有效执行，或者违约处罚的力度不够大（即X＜R-T），我们就又回到了囚徒困境，合作仍然不会出现。

在上述例子中，我们也可以通过对合作一方提供奖励的办法解决囚徒困境。在经济学上，对不合作行为的惩罚等同于对合作行为的奖励，都属于激励制度，尽管在心理学上，奖励和惩罚的效果并不总是等同的。家庭和企业内部有各种各样的奖惩制度，其目的就是解决囚徒困境问题，促进合作。对整个社会来说，往往是通过法律来对不合作行为进行处罚来促进合作。可以说，法律是解决囚徒困境、促进社会合作的重要手段，尽管如我们在第六章和第七章中将看到的，在重复博弈中，许多合作无须借助法律和正式的制度也可以实现。