PyTorch][chapter 12][李宏毅深度学习][Semi-supervised Linear Methods-1]

news2024/9/24 9:17:59

这里面介绍半监督学习里面一些常用的方案：

K-means ,HAC, PCA 等

K-means
HAC
PCA

一 K-means

【预置条件】

$X=\begin{Bmatrix} x^1 &x^2 &... & x^N \end{Bmatrix}$

N 个样本分成k 个簇

step1:

初始化簇中心点 $c_i,i=1,2,..k$ (随机从X中抽取k个样本点作为）

Repeat:

For all $x^n$ in X: 根据其到 $C_i$ （i=1,2,..k）的欧式距离:

$b_i^n=\left\{\begin{matrix}1:\, x^n\, most\, close \, c_i\\ 0: else \end{matrix}\right.$ （代表第n个样本属于第i簇）

updating all $c_i:$

$c_i=\frac{\sum_{x^n}b_i^nx^n}{\sum_{x^n}b_i^n}$

问题：

不同的初始化参数影响很大.可以通过已打标签的数据集作为 $c_i$ ,

未打标签的

二 Hierachical agglomerative Clustering(HAC)层次凝聚聚类算法

流程

1： build a tree （创建数结构）

2 clustering by threshold （通过不同的阀值进行聚类）

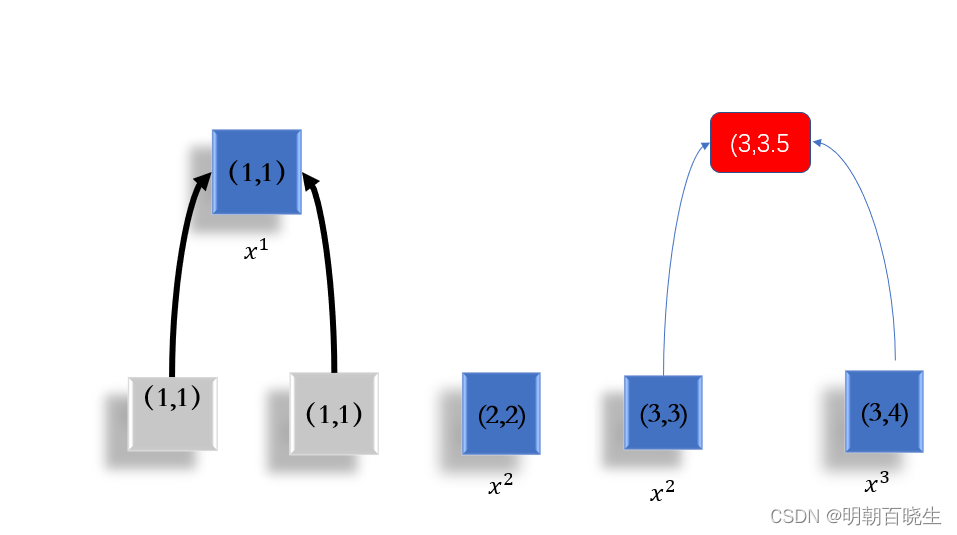
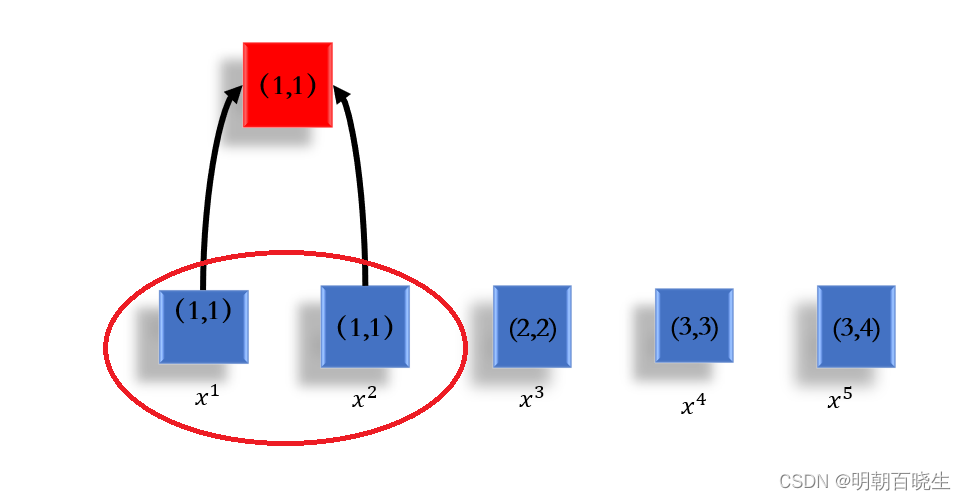
例假设有5笔data: $x^1,x^2,x^3,x^4,x^5$

build a tree

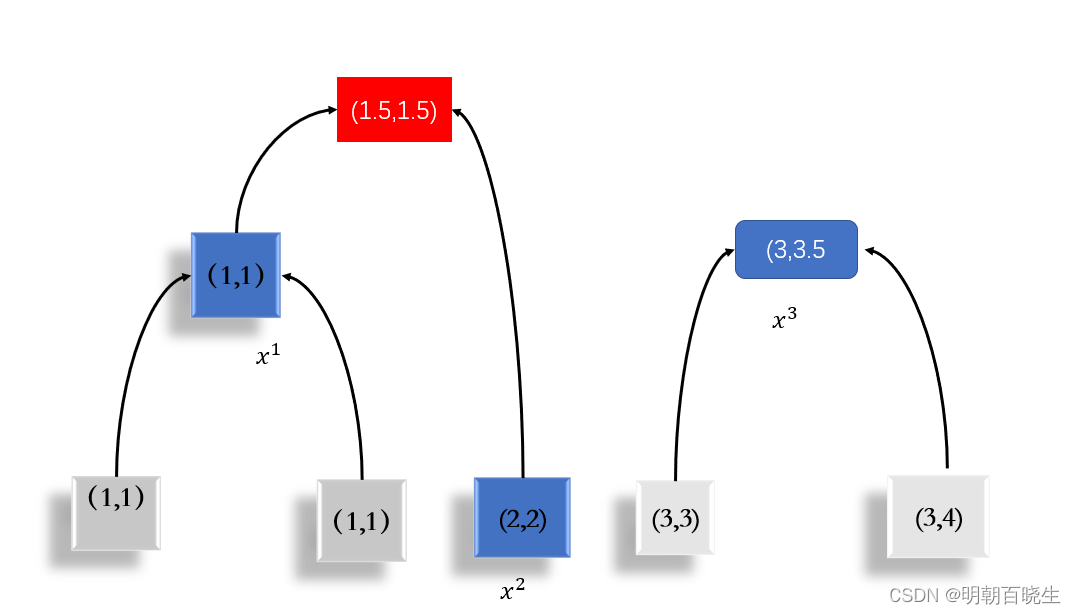
1 合并其中距离最近的两项   $x^1,x^2$



2 基于合并后的数据集 $(x^1,x^2,x^3,x^4)$ ,合并其中距离最小的两项   $x^2,x^3$



1.3 基于 $x^1,x^2,x^3$ 合并其中最小的两项 $x^1,x^3$

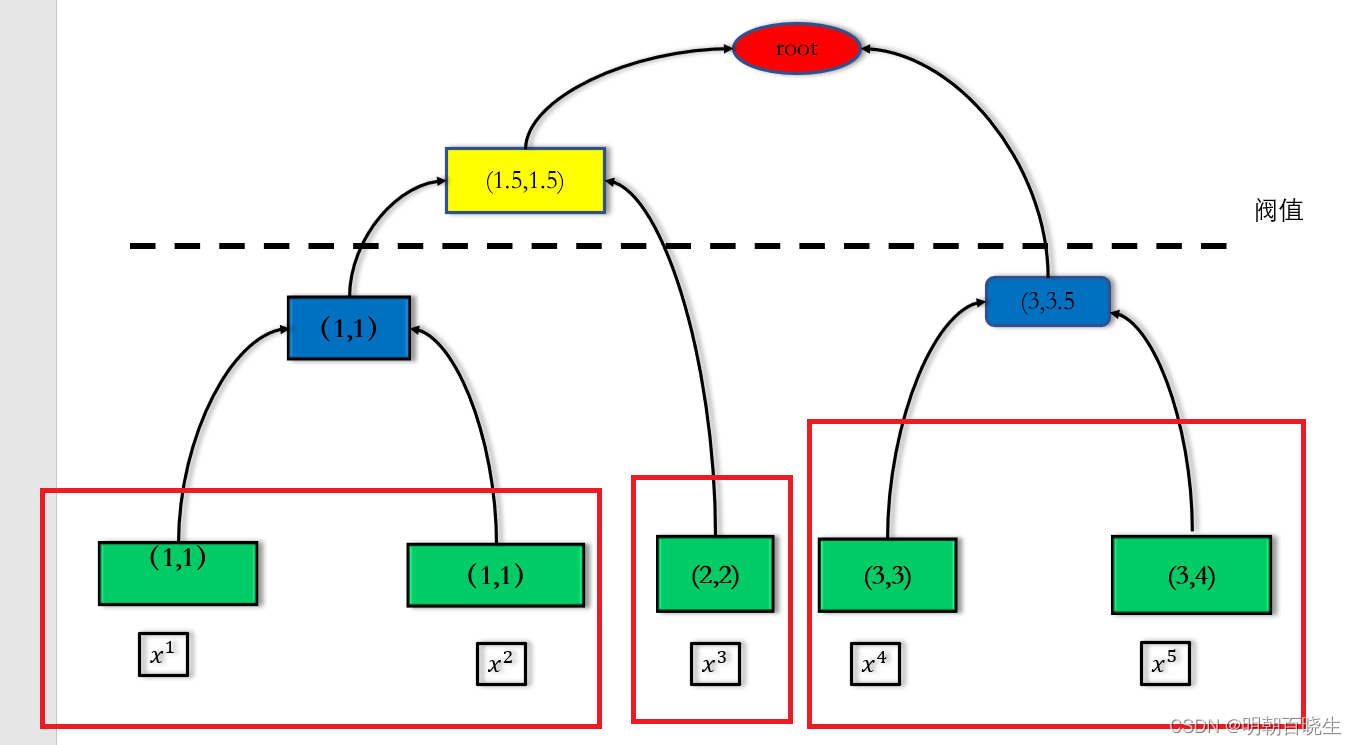
1.4 最后只剩下最后两项（N<=k),合并作为root

2 聚类（pick a threshold 选择不同的阀值进行分类）

比如阀值在黑色虚线的位置：

$x^1,x^2$ 为1类

$x^3$ 为一类

$x^4,x^5$ 为一类

# -*- coding: utf-8 -*-
"""
Created on Fri Jan 26 15:55:03 2024

@author: chengxf2
"""

import numpy as np
import math

def euler_distance(point1, point2):
    #计算欧几里德距离
    distance = 0.0
    c= point1-point2
    distance = np.sum(np.power(c,2))
    return math.sqrt(distance)


class tree:
    #定义一个节点
    def __init__(self, data, left= None,  right = None, distance=-1,idx= None,  count=1):
        
        self.x = data
        self.left = left
        self.right = right
        self.distance = distance
        self.id = idx
        self.count = count
        
        
def mergePoint(a,b):
    
    c= np.vstack((a,b))
    return c


class Hierarchical:
    
    
    
    def __init__(self, k=1):
        
        assert k>0
        self.k =k
        self.labels = None
        
    def getNearest(self, nodeList):
        #获取最邻近点
        
        N = len(nodeList)
        #print("\n N",N)
        min_dist = np.inf
       
        
        for i in range(N-1):
            for j in range(i+1, N):
                #print("\n i ",i,j)
                pointI = nodeList[i].x
                pointJ = nodeList[j].x
                d =  euler_distance(pointI, pointJ)
                if d <min_dist:
                    min_dist = d
                    closerst_point = (i, j)
        return closerst_point,min_dist
                
    def fit(self, data):
        N = len(data)
        nodeList = [ tree(data=x,idx = i) for i,x in enumerate(data)]
        currentclustid = -1
        self.labels =[-1]*N
        print(self.labels)
        
        
        while(len(nodeList)>self.k):
            
           closerest_point,min_dist = self.getNearest(nodeList)
           #print("\n closerest_point",closerest_point)
           id1, id2 = closerest_point
           node1, node2 = nodeList[id1], nodeList[id2]
           
           merge_vec =np.vstack((node1.x,node2.x))
           avg_vec = np.mean(merge_vec,axis=0)
           #print(node1.x, node2.x, avg_vec)
         
           new_node = tree(data=avg_vec, left=node1, right=node2, distance=min_dist, idx=currentclustid,
                                  count=node1.count + node2.count)
           currentclustid -= 1
           
           del nodeList[id2], nodeList[id1]
           nodeList.append(new_node)
        self.nodes = nodeList
        
           
    def calc_label(self):
         for i, node in enumerate(self.nodes):
             print("\b label",i)
             self.leaf_traversal(node, i)
             
    def leaf_traversal(self, node: tree, label):
         if node.left is None and node.right is None:
             self.labels[node.id] = label
             
         if node.left:
            
             self.leaf_traversal(node.left, label)
         if node.right:
             
             self.leaf_traversal(node.right, label)



if __name__ == "__main__":
    data = np.array([[1,1],
                     [1,1],
                     [2,2],
                     [3,3],
                     [3,4]] )
    
    net = Hierarchical(k=2)
    
    net.fit(data)
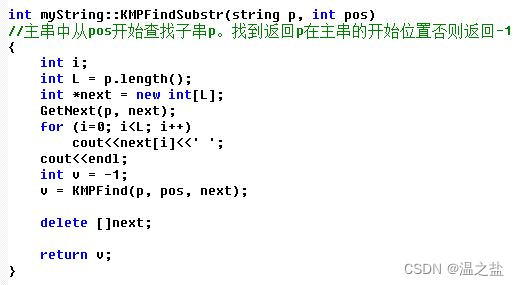
    net.calc_label()

三 PCA(Principle Component Analysis)

PCA 是机器学习里面一种主要降维方案，深度学习里面常用的是AE编码器.

如下图在3维空间里面，不同数据分布在不同的空间，通过PCA 降维到2D

空间后，不同类别的数据分布依然分布在不同的空间，数据处理起来更方便.