美国大学生数学建模竞赛（MCM）是全球知名的数学建模比赛之一，每年都吸引了来自世界各地的学生参加。在这场充满挑战的竞赛中，参赛者将面对多种题目，需要利用他们的数学建模技能来解决实际问题。下面，建模忠哥将向大家介绍MCM竞赛的常见题型和模型，希望能帮助大家更深入地理解美赛的精髓！（文章整理不易，如果你喜欢，请点赞支持！）

美赛的题型

01 美赛题目特点

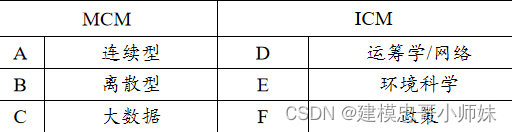
总的来说，MCM 偏自然、理工，而ICM偏社科、人文。更多的建模er更倾向于选择MCM的ABC题。MCM出的题目更偏向于运用数理知识建模解决，ICM则更偏重于运用跨学科知识。

02 近五年美赛选题占比

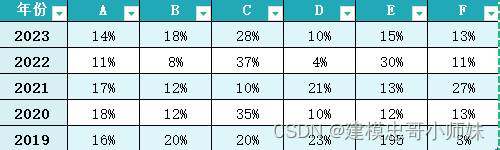
不难看出选题比例一定程度上可以反映各赛题对于选手们而言的难易程度，MCM选题总体较多，也一定程度上反映了理工背景的参赛者占比较多。

选题建议

01 A题

A题历来考察的是连续类模型图，22年的美赛考察的选题自行车赛的功率曲线，可以用微分方程与函数进行建模。以前的A题还考察过鱼群迁移等内容，这些都与美国本土的或者世界热点问题相关。更适合纯理工科队伍选择！

02 B题

B题是一道离散类问题的，考察离散优化和解方程组居多，也可以利用元胞自动机去完成。MCM的B题今年大概率可能是与重要环境因素有关，可以出现差分化的序列数据，也可能是地理位置与地理信息数据心，但条数不会很多如果条数不是很多的话，建议大家采用客观的方法去做。

03 C题

C题一直以来都是考察是数据挖掘的。数据挖掘问题的话，美赛似乎非常青睐时间数据的预测与分析应用图，尤其是金融时间序列与气象时间序列。如果条数不是很多的话，建议大家采用客观的方法去做。解决此类问题，过往很多人会采用机器学习，这是一个比较好的思路，同时如果没有一定机器学习基础的同学，也可以采用回归方程与假设检验，或者神经网络。数据的可视化在前期就应该做到位，在后面就不要再加一些过于美观但不实用的图片。数据的形式估计仍然可能是带有时间的面板数据，需要进行建模分析。在建模分析中，使用多变量回归、多变量检验以及神经网络上是非常普遍的现象。而如果想进行进一步探究，也可以用决策树类模型，最好的是能够通过概率分析等方法构建起不同物质之间作用的图模型去进行分析挖掘。

04 D题

ICM的D题是运筹与优化问题的，因为是运筹问题，我们在考虑方法的时候要考虑整数规划、多目标规划。但是实操的时候我们会更多地在评价类模型有上做文章，例如图论和博弈论。最大概率的是几个评价模型。如果大家有的人真的用到了评价类模型，要注意权重和评分。如果数据多就尽可能用客观评价，数据不多的话就更多的主观评价例如模糊综合、AHP等。

05 E题

E题的主题每年都与环境问题相关。考过森林等，这种主题经常会需要宏观时间序列数据，不过这种数据需要自己去找。如果考察关于环境治理的一些作用机理定要多查资料多找文献。数学层面的东西大概率不会考太复杂，更多的就是一些回归之类的方法，关键还是要把图片画好看，尤其是能传递环保的信息的。这个题比较建议没什么经验的人选而，尤其是有绘图、美工、广告设计等背景的同学，然后数学层面的东西它按理不会考太复杂，更多的就是一些回归之类的方法(其实回归也完全足够用了)，关键还是要把图片画好看口，尤其是能传递环保的信息的。

06 F题

F题是政治类问题中。这类题目，我们要找准切入点去下手并找准具体的突破点摆事实说话。

对于F题其实不需要太花哨方法，只要英文写作功底到位想冲击好一些的奖项完全有可能心。但在F题的突破中，数学成分不在于难，要在于恰到好处。用一个精准化的叙事体系去说一个抽象的宏观概念。

美赛中常见模型与算法

01 基础模型

线性回归，Logistic回归、多元线性回归、相关性分析

02 评价模型

层次分析，Topsis，模糊综合评价

03 预测模型

时间序列（ARIMA、指数平滑）、微分方程模型、多元线性回归、灰度预测、元胞自动机

03 降维模型

主成分分析，因子分析，随机森林，线性判别分析

04 优化模型

单/多目标规划，0-1整数规划，归一化与正则化，复杂网络优化、排队论

04 统计模型

多元分析（主成分分析、聚类分析、因子分析、判别分析、典型相关性分析等）、相关回归分析、假设检验、方差检验、贝叶斯统计

05 分类与判别算法

聚类（K-means、FCM、层次聚类），贝叶斯分类与判别，SVM，决策树

06 智能/随机算法

蒙特卡洛模拟、粒子群/蚁群算法、模拟退火、遗传算法

07 参数求解算法

遗传算法、贝叶斯搜索、极大似然估计、网格搜索

08 其他

图论算法、计算机经典算法(动态规划、回溯搜索、分治算法、分支定界等)

美赛的模型应用范围
01 物理科学

包括力学、电磁学、流体力学、量子力学等领域的建模与分析，如物体运动、电路设计、气象预测等。

02 工程与技术

涉及电子、机械、材料等工程领域的问题，如控制系统设计、结构优化、材料性能分析等。

03 生态与环境

关注生态系统、环境保护、自然资源管理等问题，如种群动力学、生态平衡、环境影响评估等。

04 经济与金融

研究经济现象和金融市场的建模与预测，例如市场供需分析、投资组合优化、经济增长模型等。

05 社会科学

探索社会问题和行为模式，如人口统计、社交网络分析、舆论传播模型等。

06 医学与生物科学

关注生物系统、医疗服务和疾病模型，如药物代谢、传染病传播、基因组分析等。

07 交通与物流

研究交通流动和物流管理问题，如交通拥堵研究、路径规划、供应链优化等。

模型的学习是无止境的，明白模型算法适用的场景，学会应用才是最关键的！

美赛的模型学习建议

01 微分方程模型：

学习微分方程的基本概念和解法，包括常微分方程和偏微分方程。

熟悉微分方程在物理、生态、经济等领域的应用，了解如何将实际问题转化为微分方程模型。

02 线性规划模型：

学习线性规划的理论基础和常见解法，如单纯形法和对偶理论等。

掌握如何建立线性规划模型，包括目标函数的设定、约束条件的建立等。

03 图论模型：

了解图论的基本概念，包括图的类型、路径、连通性等内容。

学习如何利用图论模型解决实际问题，如最短路径问题、网络流问题等。

04 统计分析模型：

掌握常见的统计分析方法，包括回归分析、方差分析、时间序列分析等。

学习如何利用统计分析模型对数据进行处理和预测。

05 随机模型：

了解随机过程的基本概念和性质，包括马尔可夫链、随机游走等内容。

学习如何建立随机模型来描述不确定性事件，并进行相应的分析和模拟。

06 优化模型：

熟悉各种优化方法，包括整数规划、非线性规划等。

学习如何利用优化模型解决实际问题，如资源分配、最佳路径选择等。

07 计算机仿真模型：

掌握计算机仿真的基本原理和方法，包括随机数生成、模型验证等内容。

学习如何利用计算机仿真模型对复杂系统进行建模和分析。

08

一些小tips：

（1）研究往年赛题及优秀论文(一定要认认真真研究几篇，这对于获奖帮助很大)；

（2）指标的数量不能少(多意味着全面)；

（3）指标的量化可以放入多个小模型，不仅丰富了文章内容，还提高了结果的准确性；

（4）先把模型建出来再考虑能不能实现；

（5）不必执着与个别找不到的数据，可以将这些指标替换，尽快进入建立模型的过程当中；

（6）做好可视化表达，往往O奖和F奖的区别就是O奖论文更加“好看”一些。