利用牛顿方法求解非线性方程（MatLab）

news2024/10/4 21:38:14

一、算法原理

1. 牛顿方法的算法原理

牛顿方法（Newton’s Method），也称为牛顿-拉弗森方法，是一种用于数值求解非线性方程的迭代方法。其基本思想是通过不断迭代来逼近方程的根，具体原理如下：

输入：要求解的非线性方程 $f (x) = 0$ ，以及初始猜测值 $x_0$ 。

输出：近似根 $x^*$ 。

初始化 $x_0$ 作为初始猜测值。
进行迭代：
- 计算 $f(x_k)$ 和 $f'(x_k)$ ，其中 $f(x_k)$ 是目标函数在当前猜测值 $x_k$ 处的值， $f'(x_k)$ 是目标函数的导数在同一点的值。
- 计算更新步骤： $x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}$ 。
- 检查终止条件，通常是检查 $f(x_{k+1})|$ 是否小于预定的精度阈值，或者检查 $x_{k+1} - x_k|$ 是否小于精度阈值。
- 如果满足终止条件，则输出 $x_{k+1}$ 作为近似根，并结束迭代。
- 否则，将 $x_{k+1}$ 作为新的猜测值，回到步骤2。

这个过程会不断重复，逐渐逼近方程 $f (x) = 0$ 的根。

2. 牛顿方法的收敛情况分析和渐进误差常数

牛顿方法的收敛性和渐进误差常数与初始猜测值以及目标函数的性质有关。以下是一些关键的考虑因素：

收敛性：

牛顿方法通常以二次收敛的速度迅速逼近根。这意味着每次迭代都会显著减小误差。
收敛性的成功与否取决于初始猜测值的选择。如果初始猜测值距离真实根足够接近，并且目标函数在根附近是光滑的（即一阶导数连续），那么方法通常会收敛。

渐进误差常数：

牛顿方法的渐进误差常数通常与目标函数的二阶导数（即曲率）有关。
如果 $f''(x^*)$ （其中 $x^*$ 是方程的真实根）不等于零且非常接近，则渐进误差常数通常较小，迭代会更快地逼近真实根。
渐进误差常数通常用 $C$ 表示，可表达为： $x_{k+1} - x^*| <= C |x_k - x^*|^2$ ，这说明误差减小得很快。

需要注意的是，牛顿方法也有一些限制和挑战，包括选择初始猜测值的困难、迭代可能发散的情况，以及对于多重根的处理。因此，在实际应用中，需要谨慎选择初始猜测值，并考虑算法的稳健性。

二、测试数据及结果

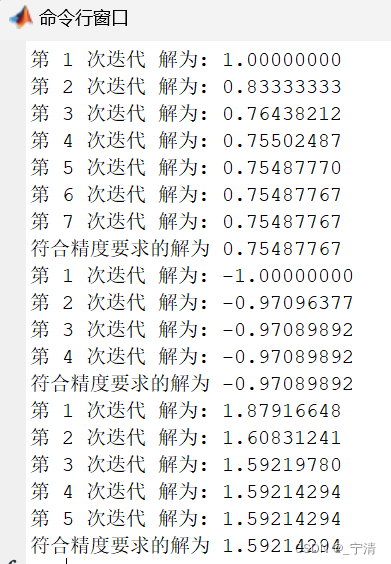
对每个方程，给出算法运行中的算法的输出结果
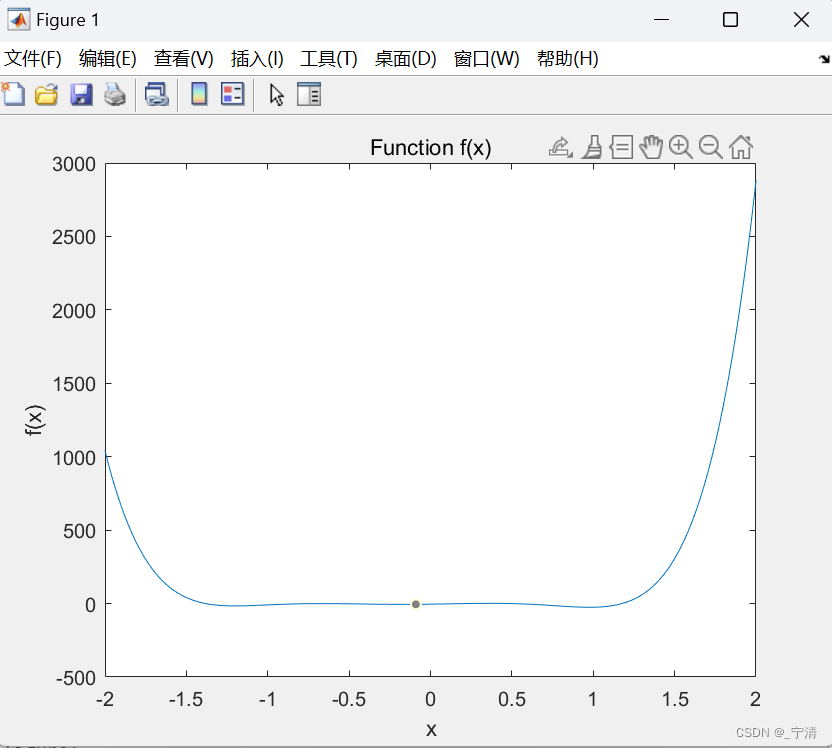
设 $f(x) = 54x^6 + 45x^5 - 102x^4 - 69x^3 + 35x^2 + 16x - 4$ ，在区间[−2,2] 上画出函数，使用牛顿方法找出该区间上的所有的5 个根。对于哪些根，牛顿方法线性收敛，哪些二次收敛？
要求：每次迭代中显示：“第x 次迭代解为: xxx”，并在停止迭代后显示“符合精度要求的解为xxx”。

% 清空工作区和命令窗口
clear;
clc;

% 创建符号变量
syms x;

% 定义目标函数
f = 54 * x^6 + 45 * x^5 - 102 * x^4 - 69 * x^3 + 35 * x^2 + 16 * x - 4;

% 绘制函数 f(x) 在区间 [-2, 2]
x_values = linspace(-2, 2, 1000);
y_values = double(subs(f, x, x_values));
figure;
plot(x_values, y_values);
title('Function f(x)');
xlabel('x');
ylabel('f(x)');

% 寻找区间 [-2, 2] 上的根
x0 = -2.0; % 初始猜测值
tol = 1e-8; % 精度要求
max_iter = 100; % 最大迭代次数
roots = []; % 存储根的数组

while x0 <= 2
    try
        root = newton_downhill(f, diff(f, x), x0, tol, max_iter);
        roots = [roots, root];
    catch
        % 如果未收敛到根，则继续下一个初始猜测值
    end
    x0 = x0 + 0.2; % 增加初始猜测值
end

% 显示找到的所有根
fprintf('找到的所有根为：\n');
disp(roots);

% 牛顿下山法函数
function root = newton_downhill(f, df, x0, tol, max_iter)
    x = x0;
    iter = 0;
    
    while iter < max_iter
        iter = iter + 1;
        f_val = double(subs(f, x));
        df_val = double(subs(df, x));
        x_new = x - f_val / df_val;
        
        fprintf('第 %d 次迭代 解为: %.8f\n', iter, x_new);
        
        if abs(x_new - x) < tol
            fprintf('符合精度要求的解为 %.8f\n', x_new);
            root = x_new;
            return;
        end
        
        x = x_new;
    end
    
    error('达到最大迭代次数，未找到满足精度要求的解');
end

函数图像：
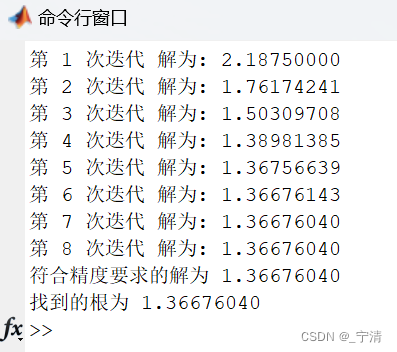
输出结果：

给出牛顿方法及牛顿下山法的运行结果。

寻找 $4x^4 - 6x^2 - \frac{11}{4} = 0$ 的根，并使用初始值 1 进行牛顿下山法求解：

function root = newton_downhill(f, df, x0, tol, max_iter)
    x = x0;
    iter = 0;
    
    while iter < max_iter
        iter = iter + 1;
        f_val = double(subs(f, x));
        df_val = double(subs(df, x));
        x_new = x - f_val / df_val;
        
        fprintf('第 %d 次迭代 解为: %.8f\n', iter, x_new);
        
        if abs(x_new - x) < tol
            fprintf('符合精度要求的解为 %.8f\n', x_new);
            root = x_new;
            return;
        end
        
        x = x_new;
    end
    
    error('达到最大迭代次数，未找到满足精度要求的解');
end

请添加图片描述

三、总结与思考

这次实验让我深入了解了牛顿迭代方法以及牛顿下山法在解决非线性方程中的应用。以下是我的总结和思考：

牛顿迭代方法：通过这次实验，我加深了对牛顿迭代方法的理解。该方法是一种迭代求根的技术，通过不断更新猜测值来逼近方程的根。它的关键是计算目标函数和其导数的值，以便求解新的猜测值。在实际应用中，选择合适的初始猜测值对于方法的收敛性至关重要。
牛顿下山法：本次实验引入了牛顿下山法，这是对传统牛顿迭代方法的改进。牛顿下山法克服了牛顿法对初始猜测值敏感的问题，通过引入步长来确保迭代方向是向着根的。这提高了方法的鲁棒性，使其更适用于实际问题。
代码实现和调试：编写MATLAB代码的过程让我学到了如何在计算机上实现数值方法。同时，我也学到了如何进行调试和错误处理。在编写代码时，要特别注意输入数据的有效性和算法的边界情况，以确保代码的稳健性。
根的重数判定：在本次实验中，我学到了如何通过计算一阶导数和二阶导数的值来判定根的重数。这是一个重要的数值分析概念，可以帮助我们理解根的收敛性和速度。
实际应用：通过解决具体的非线性方程，我认识到数值方法在实际问题中的广泛应用。无论是工程、科学还是金融领域，数值方法都是解决复杂问题的重要工具之一。