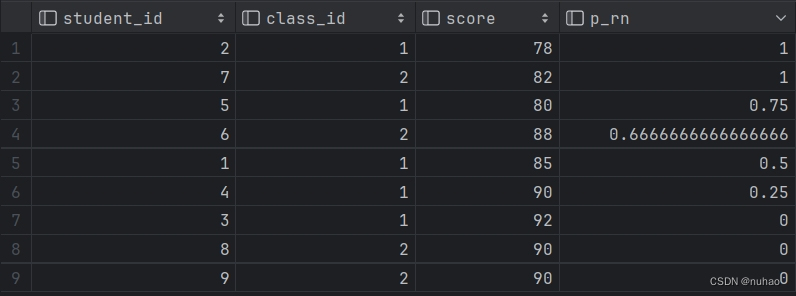
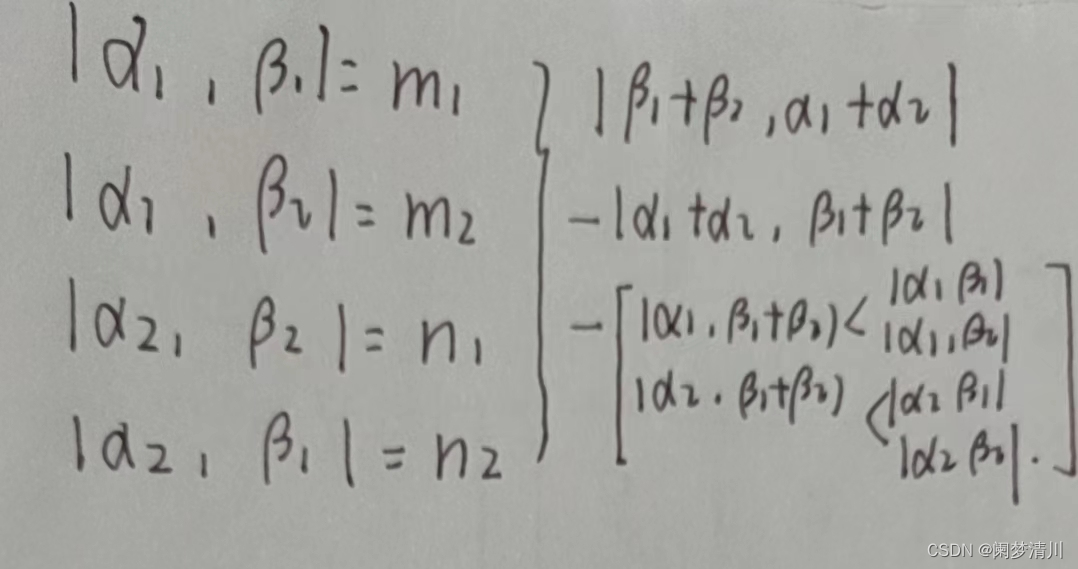不定积分这部分是为后面的定积分做准备的，整体上的框架可以分为2（定义）+3（计算方式）+3（能积出来的三个函数）

1、不定积分的概念：求某一个函数的不定积分就是求这个函数的原函数，那这里就牵扯到了存在性的问题，什么函数一定有不定积分即原函数？第一，连续的函数一定有原函数，因为连续，所以这个函数的变上限积分函数的导数等于这个函数，因此变上限积分函数就是一个原函数（这里会有一个题型，给我们一个连续的分段函数让我们求这个分段函数的原函数，我们要注意当分段求出原函数后有任意常数C，C等于多少是根据原函数一定连续得出的，因为只有函数在某一点处连续才可能可导，连续是可导的必要条件，这里不用用定义证明可导）；第二，有第一类间断点则一定没有原函数，有第二类间断点的函数有可能有原函数。

不定积分公式表：

 注意14-28这五个公式，前三个是“凑”出来的，后两个是换元出来的。

2、不定积分的三种计算方式

（1）“凑”

将函数中的某一部分拿到d的后面，也就是根据积分因子利用公式求积分，然后用积分解决问题的方法。将谁拿到后面是有学问的，如果分母是平方的形式或者是根号的形式就有可能把分母拿过去，如果分母求导=分子，那就可以直接将分子拿过去。

（2）换元

目的就是为了去掉根号、去掉e^x、去掉arcsinx等反函数，如果遇到有根号的函数，里面x是二次方我们可以用三角换元（sinx^2+cosx^2=1;1+tanx^2=sec^2;1+cotx^2=csc^x），里面如果是一次方就可以将整个根号换掉。如果遇到e^x或者是arcsinx首先看能否使用分部积分，如果不行那就整体换元。

（3）分部积分

用于两类函数乘除中，一般有多项式和指数函数、多项式和三角函数，这时候将指数函数和三角函数挪到后面；指数函数和三角函数相乘，将指数函数挪到后面；多项式和不好积分的函数相乘，一般将多项式拿到后面。拿到后面的原因是希望对前面的函数求导，使整个积分更好做。

3、三类可积分的函数

（1）有理函数的积分

有理函数首先有假分式有真分式，假分式要用多项式除法化为真分式，真分式可以分为四种，

分母可拆分的/不可拆分的，分子为常数的/分子为未知函数的。若分母可拆，则我们可以直接拆项化简计算（分母为一次，分子为常数，分子是分母的次数-1；分母是(x+1)^2，这可以设为Ax+B,也可以拆为两项，最好是拆成两项，分子都是常数），不管分子是否为常数都要这样做，但是有一种特殊情况，分母为（x^2+a^2）^2时不能拆分为多项了,直接把分母拿到d的后面去即可。若分子不可拆分子为常数，就凑成平方和平方的关系然后用公式解决。若分子不为常数，则观察分子和分母导数的关系然后加减常数并拆分计算。

（2）三角函数的积分

 

（3）无理函数的积分

这里和前面换元法中的x为1次很像