插值
插值是数学和计算机科学领域中的一种技术,用于在给定一些离散数据点的情况下,估计在这些点之间的数值。插值的目标是通过某种函数(插值函数)来逼近或拟合这些离散数据,从而使得在原始数据点之间的数值也有合理的估计。
具体来说,插值可以用于以下情况:
-
数据平滑: 通过在原始数据点之间绘制平滑的曲线,可以去除数据中的噪声或波动,提供一个更加平滑的估计。
-
数据预测: 插值可以用于预测在原始数据点之外的位置的数值,从而对未知数据点进行估计。
-
数据重构: 在数字图像处理和计算机图形学中,插值用于在像素之间生成新的像素值,以便在缩放或旋转等操作时保持图像的平滑性。
-
曲线拟合: 插值方法可以用于逼近一组数据点,生成一个平滑的曲线,以便更好地理解数据的趋势。
常见的插值方法包括线性插值、多项式插值、样条插值等。
一维插值
一维插值是指在一维空间中进行的插值操作。
在一维插值中,有一组离散的数据点,每个数据点都有一个唯一的自变量,以及一个对应的因变量。一维插值的目标是根据这些已知的数据点,推断出在自变量的连续范围内的其他位置的因变量值。
一维插值通常涉及将数据点之间的间隙填充或者对原始数据进行平滑拟合,以便于预测、分析或可视化。
插值方法的选择取决于数据的性质、所需的精度、计算资源等因素。
常见的一维插值方法:
-
线性插值: 这是一种简单的插值方法,假设在两个相邻数据点之间的因变量值之间存在线性关系。线性插值使用直线来连接相邻数据点,从而估计介于这些数据点之间的值。
-
多项式插值: 多项式插值使用一个多项式函数来逼近原始数据点,通过将多项式函数拟合到数据点上来实现插值。常见的多项式插值方法包括拉格朗日插值和牛顿插值。
-
样条插值: 样条插值将数据点之间的插值函数表示为一系列分段连续的低阶多项式(通常是三次多项式),这些多项式在数据点处相连接。这种方法可以产生平滑的曲线,并且可以控制曲线的导数,从而在拟合数据时具有更高的灵活性。
-
径向基函数插值: 这种方法使用径向基函数来拟合数据点,通过将数据点表示为这些基函数的线性组合来实现插值。径向基函数插值在某些情况下可以提供更好的逼近效果。
Python代码
import numpy as np
from scipy import interpolate
import pylab as plt
original_x = np.linspace(0, 10, 11)
# 生成一个包含11个元素的数组,表示在0到10之间均匀间隔的数列。这将用作原始数据的横坐标。
original_y = np.sin(original_x)
# 计算数组x中每个元素的正弦值,这将用作原始数据的纵坐标。
new_x = np.linspace(0, 10, 101)
# 生成一个包含101个元素的数组,表示在0到10之间均匀间隔的更细密的数列。这将用作插值后的数据的横坐标。
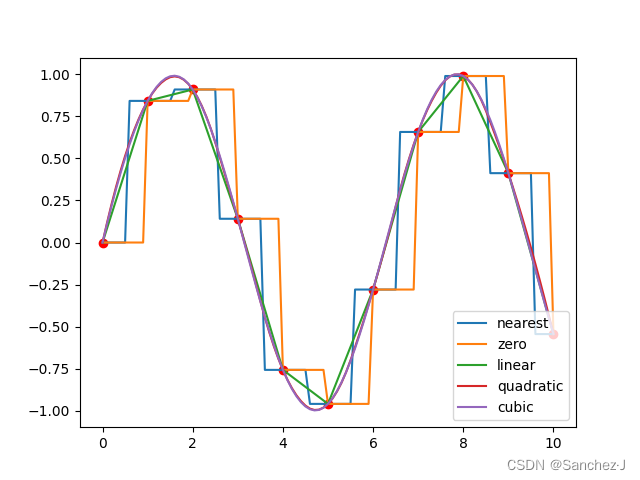
plt.plot(original_x, original_y, "ro")
# 使用红色的圆点标记绘制原始数据。"ro"表示红色圆点。
for interpolation_method in ["nearest", "zero", "linear", "quadratic", "cubic"]:
# 遍历插值方法的列表,包括"nearest"、"zero"、"linear"、"quadratic"和"cubic"。
# "nearest","zero"为阶梯插值
# linear 线性插值
# "quadratic","cubic" 为2阶、3阶B样条曲线插值
interpolation_function = interpolate.interp1d(original_x, original_y, kind=interpolation_method)
# 使用当前遍历到的插值方法创建一个插值函数f,将原始数据original_x和original_y传入。
new_y = interpolation_function(new_x)
# 使用插值函数f对新的横坐标new_x进行插值,得到插值后的纵坐标new_y。
plt.plot(new_x, new_y, label=str(interpolation_method))
# 使用当前插值方法绘制插值后的曲线。
plt.legend(loc="lower right")
plt.show()
运行结果:
二维插值
二维插值是指在二维空间中进行的插值操作。
-
双线性插值: 双线性插值假设在四个相邻的数据点之间存在平面,并使用这些平面来估计目标位置的值。这是一种简单而高效的插值方法,特别适用于规则的二维网格。
-
双三次插值: 双三次插值使用相邻的16个数据点,在目标位置周围形成一个3x3的矩形区域。然后,通过一个双三次多项式来拟合这些数据点,从而得到目标位置的插值结果。这种方法通常比双线性插值更精确,但也更计算密集。
-
二维多项式插值: 类似于一维情况,可以使用二维多项式来逼近原始数据点。这包括双变量的拉格朗日插值或者双变量的牛顿插值。
-
二维样条插值: 与一维样条插值类似,二维样条插值将数据点之间的插值函数表示为一系列分段连续的低阶多项式。这可以产生平滑的曲面,并且在拟合数据时提供更高的灵活性。
-
径向基函数插值: 类似于一维情况,径向基函数插值在二维情况下使用径向基函数来拟合数据点,从而实现插值。
Python代码
import numpy as np
from scipy import interpolate
import pylab as plt
import matplotlib as mpl
# SciPy用于科学计算
def sample_function(x, y):
return (x + y) * np.exp(-5.0 * (x ** 2 + y ** 2))
# 这定义了一个函数 sample_function(x, y),它接受两个参数 x 和 y,并返回使用数学表达式计算的值。
# 这里使用NumPy的 mgrid 创建了一个2D网格,其中 x 和 y 值在指定范围内有15个点。
grid_y, grid_x = np.mgrid[-1:1:15j, -1:1:15j]
function_values = sample_function(grid_x, grid_y)
# 计算每个网格点上的函数值 15*15的值
# 将函数 sample_function 应用于网格中的每个 x 和 y 对,
print(len(function_values[0]))
# 并将结果存储在 function_values 中。打印了 function_values 的第一行的长度。
# 三次样条二维插值
interpolated_function = interpolate.interp2d(grid_x, grid_y, function_values, kind='cubic')
# 这使用SciPy的 interp2d 使用三次样条插值进行了二维插值。
# 它创建了一个新函数 (interpolated_function) 来表示插值的值。
# 计算100*100的网格上的插值
new_x_values = np.linspace(-1, 1, 100) # x
new_y_values = np.linspace(-1, 1, 100) # y
interpolated_values = interpolated_function(new_x_values, new_y_values) # 仅仅是y值 100*100的值
# 为一个100x100的网格生成新的 x 和 y 值,并使用 interpolated_function 计算插值的值。
# 为了更明显地比较插值前后的区别,使用关键字参数interpolation='nearest'
# 关闭imshow()内置的插值运算。
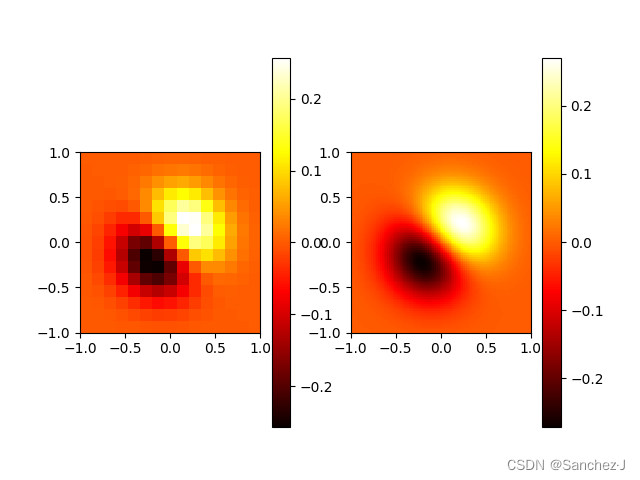
plt.subplot(121)
im1 = plt.imshow(function_values, extent=[-1, 1, -1, 1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower") # pl.cm.jet
# extent=[-1,1,-1,1]为x,y范围 favals为
plt.colorbar(im1)
plt.subplot(122)
im2 = plt.imshow(interpolated_values, extent=[-1, 1, -1, 1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
plt.colorbar(im2)
plt.show()
# 使用Matplotlib创建了两个子图,每个子图显示插值的结果 (function_values 和 interpolated_values)。
# 使用 imshow 函数显示2D数据,并添加了 colorbar 作为参考。
# 使用 interpolation='nearest' 参数可视化地比较插值前后的差异,
# origin="lower" 指定了左下角为坐标轴的原点。使用 plt.show() 显示了这两个子图。
运行结果:
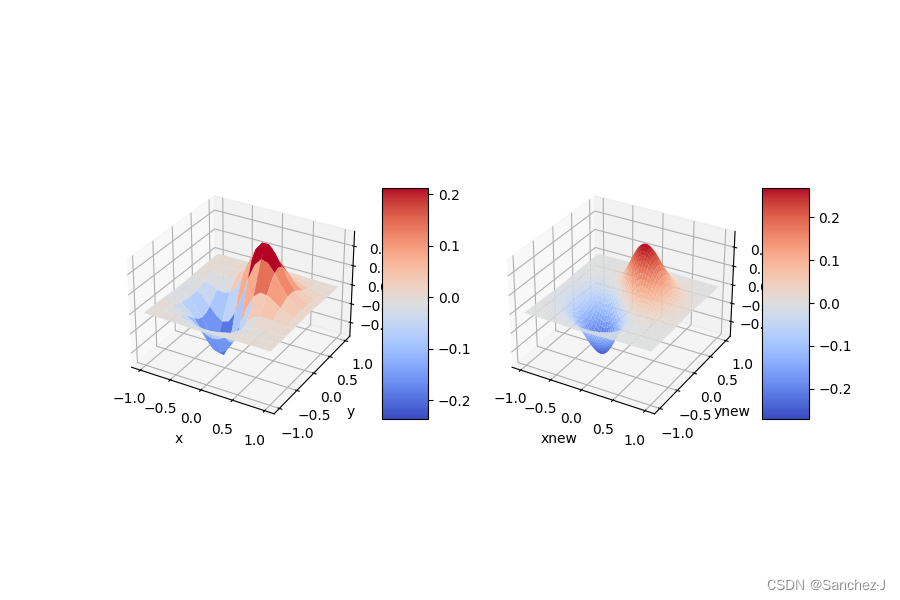
二维插值的三维表示的Python代码
详见注释
import numpy as np
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt
def target_function(x, y):
return (x + y) * np.exp(-5.0 * (x ** 2 + y ** 2))
# 目标函数
# X-Y轴分为20*20的网格
x_values = np.linspace(-1, 1, 20)
# 在[-1, 1]之间生成20个等间隔的x值。
y_values = np.linspace(-1, 1, 20)
# 在[-1, 1]之间生成20个等间隔的y值。
x_grid, y_grid = np.meshgrid(x_values, y_values)
# 生成一个20x20的网格数据,x和y分别代表网格点的x、y坐标。
function_values = target_function(x_grid, y_grid)
# 计算每个网格点上函数func的值,形成一个15x15的函数值数组。
fig = plt.figure(figsize=(9, 6))
# 创建一个图形窗口,并设置大小为(9, 6)。
# Draw sub-graph1
ax1 = plt.subplot(1, 2, 1, projection='3d')
# 在图形窗口中创建一个1行2列的子图,当前操作的是第1个子图,使用3D坐标轴。
surf1 = ax1.plot_surface(x_grid, y_grid, function_values, rstride=2, cstride=2, cmap=cm.coolwarm, linewidth=0.5, antialiased=True)
# 绘制三维表面图,使用提供的x、y、fvals数组,
# rstride和cstride控制网格线的密度,cmap设置颜色映射,
# linewidth设置线宽,antialiased开启抗锯齿。
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('f(x, y)')
plt.colorbar(surf1, shrink=0.5, aspect=5)
# 标注
# 使用二维插值方法cubic,生成新的插值函数newfunc。
interpolation_function = interpolate.interp2d(x_values, y_values, function_values, kind='cubic') # newfunc为一个函数
# 计算100*100的网格上的插值
x_new_values = np.linspace(-1, 1, 100) # 在[-1, 1]之间生成100个等间隔的新x值。
y_new_values = np.linspace(-1, 1, 100) # 在[-1, 1]之间生成100个等间隔的新y值。
function_new_values = interpolation_function(x_new_values, y_new_values) # 计算插值函数在新网格上的值,形成一个100x100的数组。
x_new_grid, y_new_grid = np.meshgrid(x_new_values, y_new_values)
# 生成新的100x100的网格数据,xnew和ynew分别代表新网格点的x、y坐标。
ax2 = plt.subplot(1, 2, 2, projection='3d')
# 在图形窗口中创建一个1行2列的子图,当前操作的是第2个子图,使用3D坐标轴。
surf2 = ax2.plot_surface(x_new_grid, y_new_grid, function_new_values, rstride=2, cstride=2, cmap=cm.coolwarm, linewidth=0.5, antialiased=True)
# 绘制三维表面图,使用新的xnew、ynew、fnew数组,其他参数同上。
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x, y)')
plt.colorbar(surf2, shrink=0.5, aspect=5) # 标注
plt.show()
运行结果: