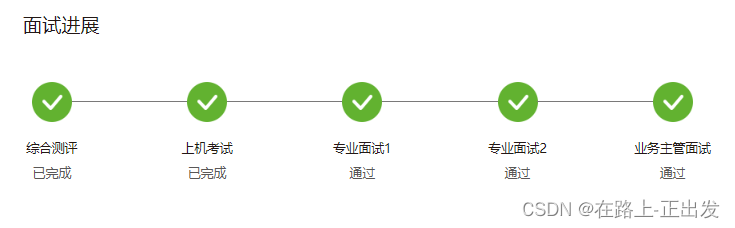
系统学习最优化理论
什么是最优化问题?
决策问题:
(1)决策变量
(2)目标函数(一个或多个)
(3)一个可由可行策略组成的集合(等式约束或者不等式约束)
最优化问题基本形式

1 最优化问题分类
根据可行域S划分:无约束/约束优化

根据函数的性质划分:线性规划/非线性规划

根据可行域的性质划分:离散优化/连续优化

根据函数的向量性质划分:单目标/多目标优化

根据规划问题有关信息的确定性划分:随机/模糊/确定性规划

2 预备知识
凸优化理论:凸集、凸函数、凸优化问题- 无约束优化问题的算法
- 约束优化的
最优性条件及对偶理论 - 线性规划、二次规划算法
- 约束优化的
罚函数方法
2.1 线性代数知识
最优化问题的表述和求解过程中矩阵是必不可少的
线性空间
通常考虑的线性空间是n维(列)向量空间
R
n
R^n
Rn,记n维列向量为:
x
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
T
x=(x_1,x_2,...,x_n)^T
x=(x1,x2,...,xn)T
欧氏空间Euclid
矩阵
若
A
A
A为
n
n
nX
n
n
n矩阵,且
A
A
A满足
A
T
=
A
A^T=A
AT=A,则称A为对称矩阵;若对于一切
x
≠
0
x≠0
x=0,均有
x
T
A
x
>
0
x^TAx>0
xTAx>0,则称A为正定矩阵;若对一切
x
x
x,均有
x
T
A
x
≥
0
x^TAx≥0
xTAx≥0,则称
A
A
A为半正定矩阵。
2.2 多元函数分析
分析多元函数在一点附近的特性,在该点处的线性近似和二次近似对于考虑这个函数在该点处的最优性条件是非常有用的。
函数f(x)在x处的一阶导数和梯度,记 g ( x ) = ▽ f ( x ) g(x)=\bigtriangledown f(x) g(x)=▽f(x)(g(x)为列向量)
函数f(x)在x处的二阶导数或海森矩阵,记为 ▽ 2 f ( x ) \bigtriangledown^2f(x) ▽2f(x),若f(x)对x各变元的所有二阶偏导数都连续,此时 ▽ 2 f ( x ) \bigtriangledown^2f(x) ▽2f(x)为对称矩阵。
3 凸集
m
i
n
f
(
x
)
s
.
t
.
x
∈
S
min\ f(x)\\ s.t.\ x∈S
min f(x)s.t. x∈S
f
(
x
)
f(x)
f(x)一维:

f
(
x
)
f(x)
f(x)二维:
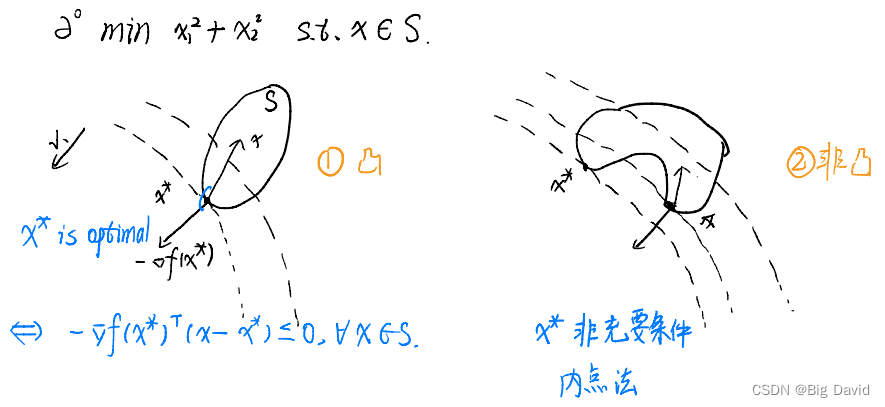
3.1 凸集的定义

3.2 常见凸集


保持凸性的运算


3.3 凸集合的性质


3.4 凸集之Farkas引理