摘 要:在分析无刷直流电机(BLDC)数学模型的基础上,提出了无刷直流电机系统仿真建模的
新方法。在Matlab/Simulink 中,建立独立的功能模块,如BLDC 本体模块、电流滞环控制模块、
速度控制模块等,再进行功能模块的有机整合,搭建无刷直流电机系统的仿真模型。为保证仿真
快速性和有效性,模型采用分段线性法生成梯形波反电动势,系统采用双闭环控制:速度环采用
PI 控制,电流环采用滞环电流控制。仿真结果证明了该方法的有效性,同时也适用于验证其他控
制算法的合理性,为实际电机控制系统的设计和调试提供了新的思路。
关键词:无刷直流电机(BLDC);仿真建模;MATLAB;分段线性法
引 言1
随着电力电子技术、微电子技术、新型电机控制理论和稀土永磁材料的快速发展,永磁无刷直流电动机得以迅速推广。因其体积小、性能好、结构简单、可靠性高、输出转矩大等特点,永磁无刷直流电动机受到了广泛关注。随着永磁无刷直流电机应用领域的不断拓宽,对电机控制系统设计要求越来越高,既要考虑成本低廉、控制算法合理,又需兼顾控制性能好、开发周期短。因此,如何建立有效的永磁无刷直流电机控制系统的仿真模型成为电机控制算法设计人员迫切需要解决的关键问题,从而,对于建立电机控制系统仿真模型方法的研究具有十分重要的意义。永磁直流电动机根据永磁体在气隙中产生的磁场波形不同,可分为正弦波永磁无刷直流电机(PMSM)和方波永
磁无刷直流电机(BLDC)。PMSM 的气隙磁密为正弦波分布,反电动势和相电流波形皆为正弦波;而BLDC 的气隙磁密为方波分布,反电动势波形为梯形波,相电流波形为方波。Matlab针对电气传动控制领域所设计的工具箱SimPowerSystem Toolbox2.3已提供了PMSM的电机模型,但没有给出 BLDC 的电机模型。因此,本文在分析无刷直流电机数学模型的基础上,借助于Matlab 强大的仿真建模能力,在Matlab/Simulink 中建立了BLDC 控制系统的仿真模型。对于在 Matlab 中进行BLDC 建模仿真方法的研究已受到广泛关注,例如:已有提出采用节点电流法对电机控制系统进行分析,通过列写m 文件,建立BLDC 仿真模型,这种方法实质上是一种整体分析法,因而这一模型基础上修改控制算法或添加、删除闭环就显得很不方便;为了克服这一不足,在Matlab/Simulink 中构造独立的功能模块,通过模块组合进行BLDC 建模,这一方法可观性好,在原有的建模基础上添加、删除闭环或改变控制策略都十分便捷,但该方法采用快速傅立叶变换(FFT)方法求取反电动势,使得仿真速度很受限制。本文提出了一种新型的BLDC 建模方法,将控制单元模块化,在Matlab/Simulink 建立独立的功能模块:BLDC 本体模块、电流滞环控制模块、速度控制模块、参考电流模块、转矩计算模块和电压逆变模块,对这些功能模块进行有机整合,即可搭建出无刷直流电机系统的仿真模型。在建模过程中,梯形波反电动势的求取方法一直是较难解决的问题,本文采用分段线性法成功地化解了这一难点,克服了建模方法存在的不足。仿真结果证明了该种新型建模方法的快速性和有效性,采用该方法不仅可以节省控制方案的设计周期,快速验证所设计的控制算法;更可以充分利用计算机仿真的优越性,通过修改系统参变量或人为加入不同扰动因素来考察不同实验条件下电机系统的动、静态性能,也可以模拟相同的实验条件,比较不同控制策略的优劣,为分析和设计BLDC 控制系统提供了有效的手段和工具。
1 永磁无刷直流电动机(BLDC)的数学模型
以二相导通星形三相六状态为例,分析 BLDC 的数学模型及电磁转矩等特性。为了便于分析,假定:
(1) 三相绕组完全对称,气隙磁场为方波,定子电流、转子磁场分布皆对称;
(2) 忽略齿槽、换相过程和电枢反应等的影响;
(3) 电枢绕组在定子内表面均匀连续分布;
(4) 磁路不饱和,不计涡流和磁滞损耗。
则三相绕组的电压平衡方程[5]可表示为:

式中:![]() —定子相绕组电压(V);
—定子相绕组电压(V);![]() —定子相绕组电流(A);
—定子相绕组电流(A);![]() —定子相绕组电动势(V);L—每相绕组的自感(H);M—每两相绕组间的互感
—定子相绕组电动势(V);L—每相绕组的自感(H);M—每两相绕组间的互感
(H);p—微分算子![]() 。一相方波电流和梯形波反电动势如图1 所示。
。一相方波电流和梯形波反电动势如图1 所示。
三相绕组为星形连接,且没有中线,则有
![]() 并且
并且
![]() 将式(2)和式(3)代入式(1),得到电压方程为
将式(2)和式(3)代入式(1),得到电压方程为


永磁无刷直流电动机的电磁转矩是由定子绕组中的电流与转子磁钢产生的磁场相互作用而产生的。定子绕组产生的电磁转矩表达式为

由(5)式可看出,无刷直流电动机的电磁转矩方程与普通直流电动机相似,其电磁转矩大小与磁通和电流幅值成正比,所以控制逆变器输出方波电流的幅值即可控制无刷直流电动机的转矩。为产生恒定的电磁转矩,要求定子电流为方波,反电动势为梯形波,且在每半个周期内,方波电流的持续时间为120°电角度,梯形波反电动势的平顶部分也为120°电角度,两者应严格同步。
2 基于 MATLAB的BLDC系统模型的建立
在 Matlab6.5 的Simulink 环境下,利用SimPowerSystemToolbox2.3 丰富的模块库,在分析BLDC 数学模型的基础上,提出了建立BLDC 控制系统仿真模型的方法,系统设计框图如图3 所示。

如图 3 所示,BLDC 建模仿真系统采用双闭环控制方案:转速环由PI 调节器构成,电流环由电流滞环调节器构成。根据模块化建模的思想,将图3 所示的控制系统分割为各个功能独立的子模块,图4 即为BLDC 建模的整体控制框图,其中主要包括:BLDC 本体模块、电流滞环控制模块、速度控制模块、参考电流模块、转矩计算模块和电压逆变模块。通过这些功能模块的有机整合,就可在Matlab/Simulink 中搭建出BLDC 控制系统的仿真模型,并实现双闭环的控制算法,如图4 所示,图中各功能模块的作用与结构简述如下。

图 4 Matlab/Simulink 中BLDC 仿真建模整体控制框图
3 仿真结果
本文基于 Matlab/Simulink 建立了BLDC 控制系统的仿真模型,并对该模型进行了BLDC 双闭环控制系统的仿真。仿真中,BLDC 电机参数设置为:定子相绕组电阻R=1Ω,定子相绕组自感L=0.02L,互感M=-0.0067H,转动惯量J=0.005kg.m2,额定转速ne=2500r/min ,极对数np=1,200V 直流电源供电。为了验证所设计的 BLDC 控制系统仿真模型的静、动态性能,系统空载起动,待进入稳态后,在t=0.5s 时突加负载TL=5Nm,可得到系统转速、转矩、A 相电流和A 相反电动势仿真曲线如图10-13 所示。
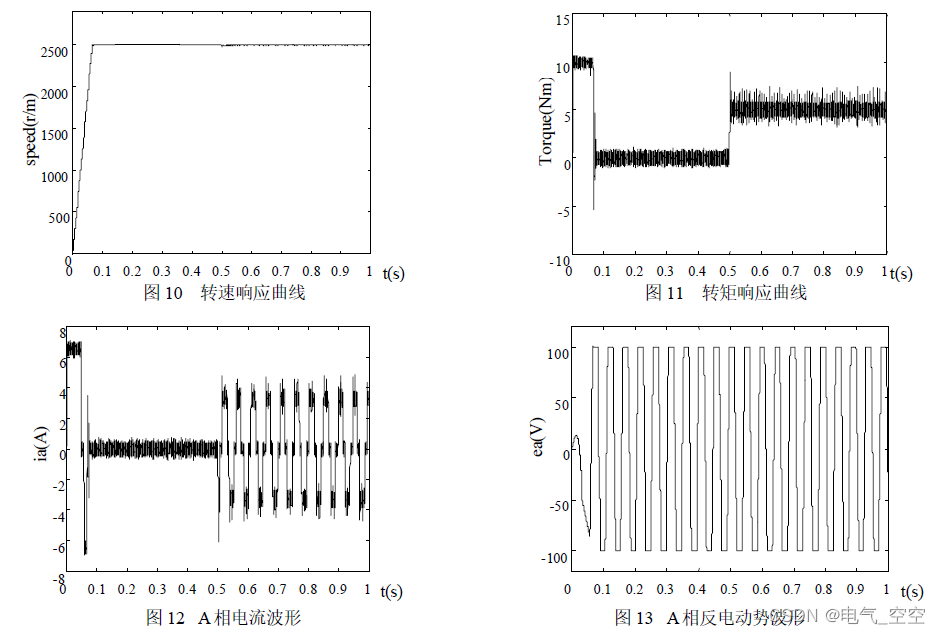
由仿真波形可以看出,在 ne=2500r/min 的参考转速下,系统响应快速且平稳,相电流和反电动势波形较为理想。仿真波形图10、11 表明:起动阶段系统保持转矩恒定,因而没有造成较大的转矩和相电流冲击,参考电流的限幅作用十分有效;空载稳速运行时,忽略系统的摩擦转矩,因而此时的电磁转矩均值为零;在t=0.5s 时突加负载,转速发生突降,但又能迅速恢复到平衡状态,稳态运行时无静差。仿真波形图11 中,突加负载后,负载转矩有较大的脉动,这主要是由电流换向和电流滞环控制器的频繁切换造成的。仿真结果证明了本文所提出的这种新型BLDC 仿真建模方法的有效性。
4 结论
本文在分析 BLDC 数学模型的基础上,提出了一种新型的基于 Matlab 的BLDC 控制系统仿真建模的方法,将该方法应用于Simulink 环境下BLDC 模型的设计,采用经典的速度、电流双闭环控制方法对该建模方法进行了测试,仿真结果表明:波形符合理论分析,系统能平稳运行,具有较好的静、动态特性。采用该BLDC 仿真模型,可以十分便捷地实现、验证控制算法,改换或改进控制策略也十分简单,只需对部分功能模块进行替换或修改,因此,它为分析和设计BLDC 控制系统提供了有效地手段和工具,也为实际电机控制系统的设计和调试提供了新的思路。