3MN: Three Meta Networks for Multi-Scenario and Multi-Task Learning in Online Advertising Recommender Systems
背景
推荐领域的多场景多任务学习:维护单模型即可节省资源也可节省人力;各个场景的数据共享,理论上面学习是更加充分的
问题&挑战
- 怎么学习复杂的多任务、多场景之间的关系MSMT(Multi-Scenario Multi-Task Learning),即(场景-场景、场景-任务、任务-任务之间的相互关系)
- 单个模型如何解决多个场景多个任务的不同数据分布问题(例如,来自不同媒体的用户不同,点击广告的意愿也不同;即使用户来自同一媒体,他们也点击广告的意愿通常会与他们下载应用程序的意愿不同)
- 不同场景下的样本分布严重不均,来自主流媒体的样本通常比小规模媒体要多得多,样本充足的场景怎么帮助哪些相关但是样本少的场景
解决方案
Three Meta Networks-based solution (3MN)
提出的三个场景自适应组件解决了挑战1,极大地提升了多任务的性能。第二个挑战由场景任务自适应主干网络及分类器解决,主干网络利用场景任务信息抽取分场景的任务特有、任务共享特征,场景自适应分类器利用这些特征提升分场景的多任务预测性能。第三个挑战由场景自适应embedding层解决,以一个自动的方式来选择不同场景下的Embedding维度。
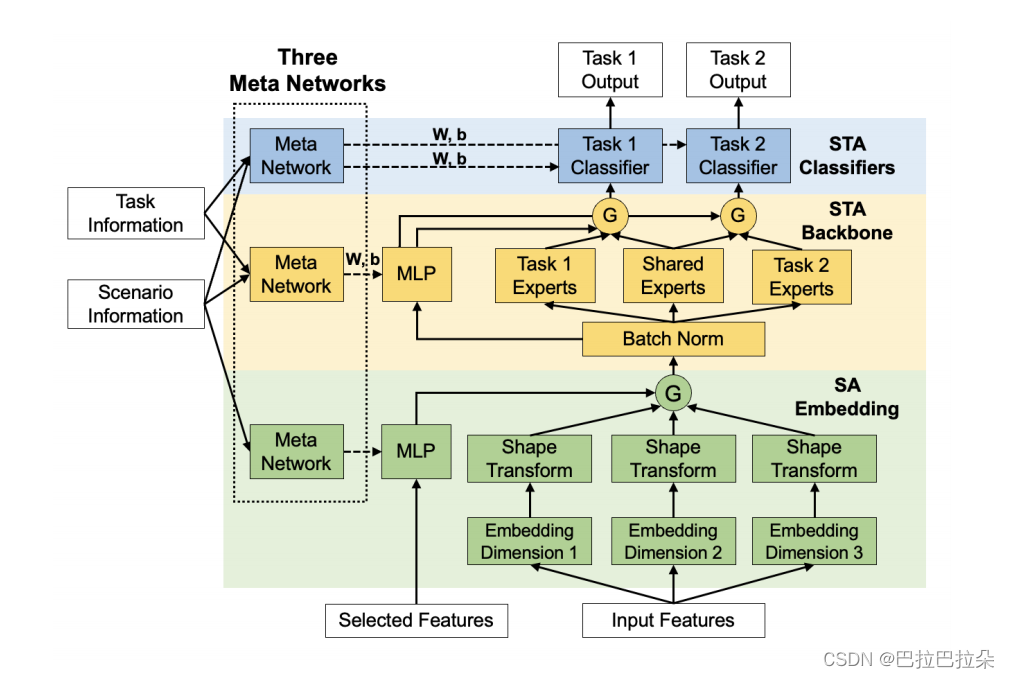
点评:这篇文章是把元网络用到了极致,底层、中间层、顶层都注入了场景知识,实现场景的自适应匹配
方案详情
Scenario-Adaptive Embedding Layer
step1:Unified Embedding Dimensions.
以往的每个特征在Embedding层都映射到一个固定维度的特征向量上面,这里为了场景自适应匹配维度,设计了根据场景来选择合适的维度。
具体就是预先设置一组维度列表
{
α
1
,
α
2
,
.
.
.
,
α
a
}
\{\alpha_1, \alpha_2, ..., \alpha_a\}
{α1,α2,...,αa},长度为
∣
α
∣
|\alpha|
∣α∣,对于每个输入的特征,产生
∣
α
∣
|\alpha|
∣α∣个embedding向量
x
i
=
E
m
b
e
d
d
i
n
g
i
(
x
)
i
∈
{
1
,
2
,
.
.
.
,
∣
α
∣
}
\mathbf x_i = \mathrm {Embedding}_i(\mathbf x) \ \ \ \ i \in \{1,2, ..., |\alpha|\}
xi=Embeddingi(x) i∈{1,2,...,∣α∣}
然后使用一个形状转换层将形状转为统一的尺寸
x
i
~
=
x
i
W
i
+
b
i
i
∈
{
1
,
2
,
.
.
.
,
∣
α
∣
}
\widetilde {\mathbf x_i} = \mathbf x_i \mathbf W_i + \mathbf b_i \ \ \ \ i \in \{ 1,2,..., |\alpha| \}
xi
=xiWi+bi i∈{1,2,...,∣α∣}
然后使用BatchNorm对这
∣
α
∣
|\alpha|
∣α∣个向量进行处理,避免出现由形状转换引起的极端数值变化
x
i
‾
=
B
a
t
c
h
N
o
r
m
(
x
i
~
)
\overline {\mathbf x_i} = \mathrm {BatchNorm} ( \widetilde {\mathbf x_i} )
xi=BatchNorm(xi
)
step2:Scenario-Adaptive Embedding Dimension Selection
然后将
∣
α
∣
|\alpha|
∣α∣个向量进行加权求和得到特征最终的embedding向量
x
s
a
e
m
b
=
∑
i
=
1
∣
α
∣
p
i
‾
x
i
‾
\mathbf x_{sa_emb} = \sum_{i=1}^{|\alpha|} \overline {\mathbf {p_i}} \overline {\mathbf {x_i}}
xsaemb=∑i=1∣α∣pixi
这里的权重
p
i
‾
\overline {\mathbf {p_i}}
pi是由元网络得到的,而元网络的输入是场景特征,因此能做到场景自适应的选择不同Embedding维度。
W
1
,
b
1
,
W
2
,
b
2
=
M
e
t
a
N
e
t
e
m
b
(
x
s
c
e
n
e
)
\mathbf W_1, \mathbf b_1, \mathbf W_2, \mathbf b_2 = \mathrm {MetaNet_{emb}} (\mathbf x_{scene})
W1,b1,W2,b2=MetaNetemb(xscene)
p = f 1 ( σ ( W 2 T ( σ ( W 1 T E m b e d d i n g ( x s e l e c t e d ) ) + b 1 ) + b 2 ) ) \mathbf p = f_1(\sigma ( \mathbf W_2^T( \sigma(\mathbf W^T_1 \mathrm {Embedding}( \mathbf x_{selected})) + b_1) + \mathbf b_2)) p=f1(σ(W2T(σ(W1TEmbedding(xselected))+b1)+b2))
其中 x s e l e c t e d \mathbf x_{selected} xselected是用户及item的一些频次统计特征,也就是基于user、item、scene三者来选择不同维度的Embedding
p
∈
R
∣
α
∣
∗
n
f
i
e
l
d
\mathbf p\in R^{|\alpha| * n^{field}}
p∈R∣α∣∗nfield,先reshape成
R
n
f
i
e
l
d
∗
∣
α
∣
R^{n^{field}*|\alpha| }
Rnfield∗∣α∣,然后经过softmax后再拆分成
α
\alpha
α
p
1
‾
,
p
2
‾
,
.
.
.
,
p
∣
α
∣
‾
=
S
p
l
i
t
(
S
o
f
t
m
a
x
(
R
e
s
h
a
p
e
(
p
)
)
)
\overline {\mathbf {p_1}},\overline {\mathbf {p_2}},...,\overline {\mathbf {p_{|\alpha|}}} = \mathrm {Split} (\mathrm { Softmax}( \mathrm {Reshape ( \mathbf p)} ))
p1,p2,...,p∣α∣=Split(Softmax(Reshape(p)))
Scenario&Task-Adaptive Backbone Network
类似于PLE的结构,有任务特有和任务共享的专家
Shared and Specific Experts.
首先BN处理下
x
b
n
=
B
a
t
c
h
N
o
r
m
(
x
s
a
e
m
b
)
\mathbf x_{bn} = \mathrm {BatchNorm} (\mathbf x_{sa_emb})
xbn=BatchNorm(xsaemb)
然后任务特有的专家和任务共享的专家
e
i
,
j
=
T
a
s
h
S
p
e
c
E
x
p
e
r
t
i
(
x
b
n
)
\mathbf e_{i,j} = \mathrm {TashSpecExpert_i}(\mathbf x_{bn})
ei,j=TashSpecExperti(xbn)
s
k
=
T
a
s
h
S
h
a
r
e
E
x
p
e
r
t
k
(
x
b
n
)
\mathbf s_{k} = \mathrm {TashShareExpert_k}(\mathbf x_{bn})
sk=TashShareExpertk(xbn)
Scenario&Task-Adaptive Expert Selection
对专家进行加权融合
x
t
i
~
=
p
t
i
~
X
t
i
\widetilde {\mathbf x_{t_i}} = \widetilde{ \mathbf p_{t_i}} \mathbf X_{t_i}
xti
=pti
Xti
这里的专家即
X
t
i
=
[
e
i
,
1
T
,
e
i
,
2
T
,
.
.
.
,
e
i
,
n
n
i
T
,
s
1
T
,
s
2
T
,
.
.
.
,
s
n
s
e
T
]
\mathbf X_{t_i} = [ \mathbf e_{i,1}^T, \mathbf e_{i,2}^T, ..., \mathbf e_{i,n^{n_i}}^T, \mathbf s_1^T, \mathbf s_2^T, ..., \mathbf s_{n^{se}}^T]
Xti=[ei,1T,ei,2T,...,ei,nniT,s1T,s2T,...,snseT]
各个专家的权重 p t i ~ \widetilde{ \mathbf p_{t_i}} pti 是场景自适应的,也是由元网络得到的,元网络的输入是场景信息和任务信息
p
t
i
=
f
2
(
σ
(
W
2
T
(
σ
(
W
1
T
E
m
b
e
d
d
i
n
g
(
x
b
n
)
)
+
b
1
)
+
b
2
)
)
\mathbf p_{t_i} = f_2(\sigma ( \mathbf W_2^T( \sigma(\mathbf W^T_1 \mathrm {Embedding}( \mathbf x_{bn})) + b_1) + \mathbf b_2))
pti=f2(σ(W2T(σ(W1TEmbedding(xbn))+b1)+b2))
W
1
,
b
1
,
W
2
,
b
2
=
M
e
t
a
N
e
t
b
a
c
k
b
o
n
e
(
[
x
s
c
e
n
e
∣
∣
x
t
a
s
k
]
)
\mathbf W_1, \mathbf b_1, \mathbf W_2, \mathbf b_2 = \mathrm {MetaNet_{backbone}} ([\mathbf x_{scene} \ || \ \mathbf x_{task}])
W1,b1,W2,b2=MetaNetbackbone([xscene ∣∣ xtask])
p t i ‾ = S o f t m a x ( p t i ) \overline {\mathbf p_{t_i}} = \mathrm {Softmax}(\mathbf p_{t_i}) pti=Softmax(pti)
Scenario&Task-Adaptive Classifiers
得到专家的加权输出后,再通过各自任务的tower层,得到最终任务的输出
o
t
i
=
f
3
(
σ
(
W
2
T
(
σ
(
W
1
T
E
m
b
e
d
d
i
n
g
(
x
t
i
~
)
)
+
b
1
)
+
b
2
)
)
\mathbf o_{t_i} = f_3(\sigma ( \mathbf W_2^T( \sigma(\mathbf W^T_1 \mathrm {Embedding}( \widetilde {\mathbf x_{t_i}})) + b_1) + \mathbf b_2))
oti=f3(σ(W2T(σ(W1TEmbedding(xti
))+b1)+b2))
W
1
,
b
1
,
W
2
,
b
2
=
M
e
t
a
N
e
t
c
l
a
s
s
i
f
y
(
[
x
s
c
e
n
e
∣
∣
x
t
a
s
k
]
)
\mathbf W_1, \mathbf b_1, \mathbf W_2, \mathbf b_2 = \mathrm {MetaNet_{classify}} ([\mathbf x_{scene} \ || \ \mathbf x_{task}])
W1,b1,W2,b2=MetaNetclassify([xscene ∣∣ xtask])
MSMT Meta Networks
详解 meta 网络也有三个组件, meta embedding layer, meta backbone network, and meta fully-connected layers
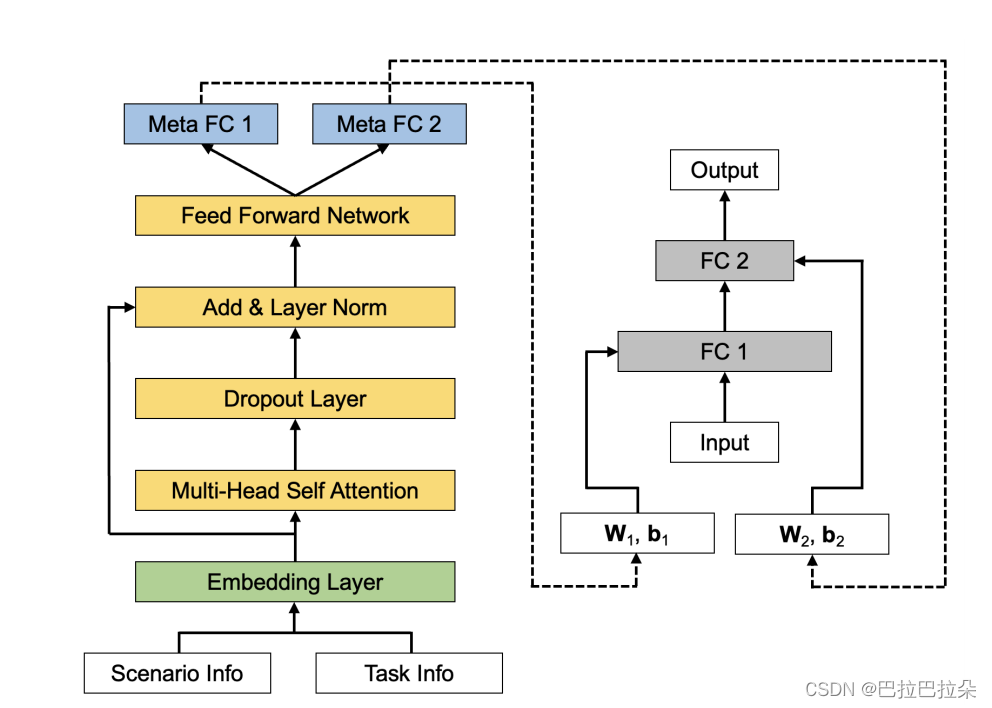
meta embedding layer
x
e
m
b
=
E
m
b
e
d
d
i
n
g
(
[
x
s
c
e
n
e
∣
∣
x
t
a
s
k
]
)
\mathbf x_{emb} = \mathrm {Embedding} ([\mathbf x_{scene} \ || \ \mathbf x_{task}])
xemb=Embedding([xscene ∣∣ xtask])
meta backbone network
x m e t a = L a y e r N o r m ( D r o p o u t ( M H ( x e m b ) ) ) + x e m b \mathbf x_{meta} = \mathrm {LayerNorm} ( \mathrm {Dropout} ( \mathrm {MH} (\mathbf x_{emb}) ) ) + \mathbf x_{emb} xmeta=LayerNorm(Dropout(MH(xemb)))+xemb
x m e t a ‾ = M L P ( x m e t a ) \overline {\mathbf x_{meta}} = \mathrm {MLP} (\mathbf x_{meta}) xmeta=MLP(xmeta)
meta fully-connected layers 得到最终的权重
W
i
,
b
i
=
W
i
m
e
t
a
x
m
e
t
a
‾
+
b
i
m
e
t
a
i
∈
{
1
,
2
}
\mathbf W_i, \mathbf b_i = \mathbf W_i^{meta} \overline {\mathbf x_{meta}} + \mathbf b_i^{meta} \ \ \ i \in \{1,2\}
Wi,bi=Wimetaxmeta+bimeta i∈{1,2}
其中
W
i
m
e
t
a
\mathbf W_i^{meta}
Wimeta和
b
i
m
e
t
a
\mathbf b_i^{meta}
bimeta是元网络FCN的参数
这里产出的
W
i
,
b
i
\mathbf W_i, \mathbf b_i
Wi,bi就是上面用到的权重
实验&消融分析
数据集
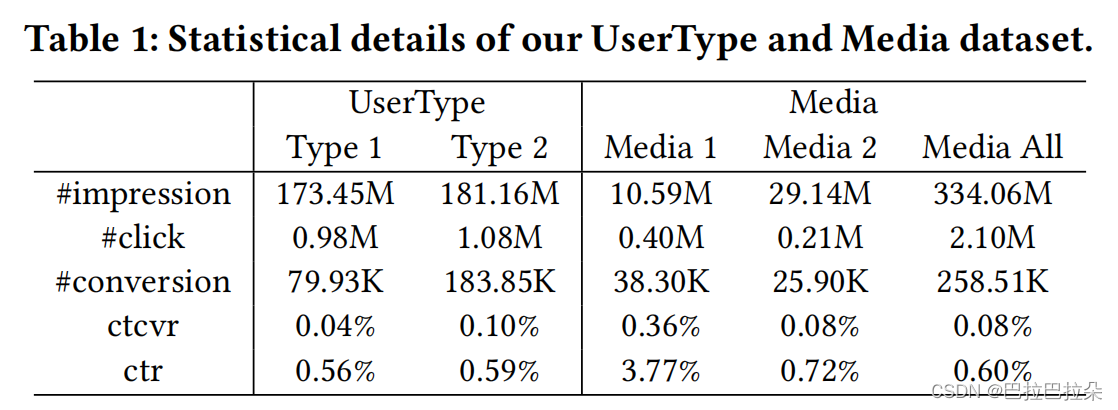
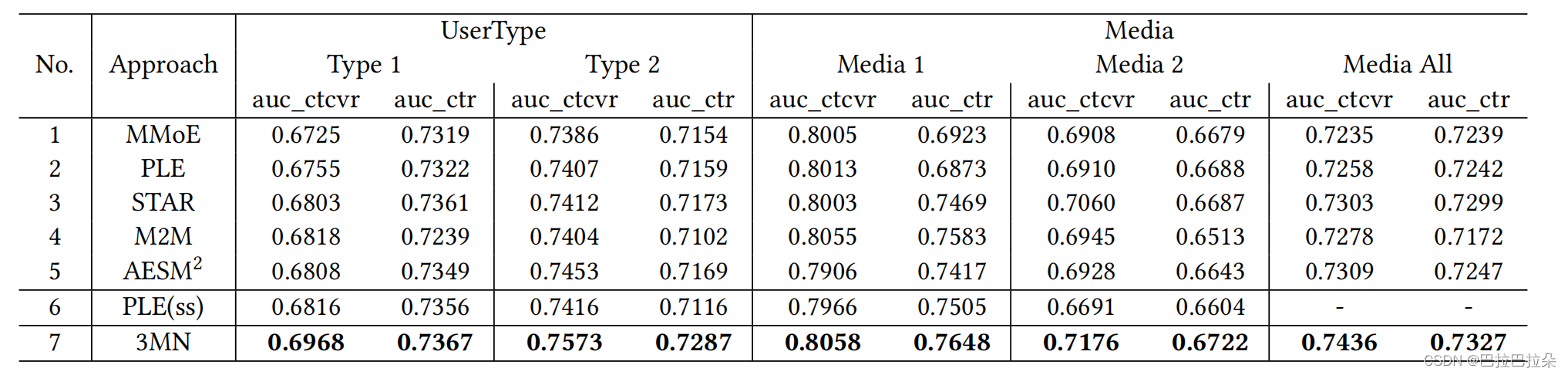
实验效果
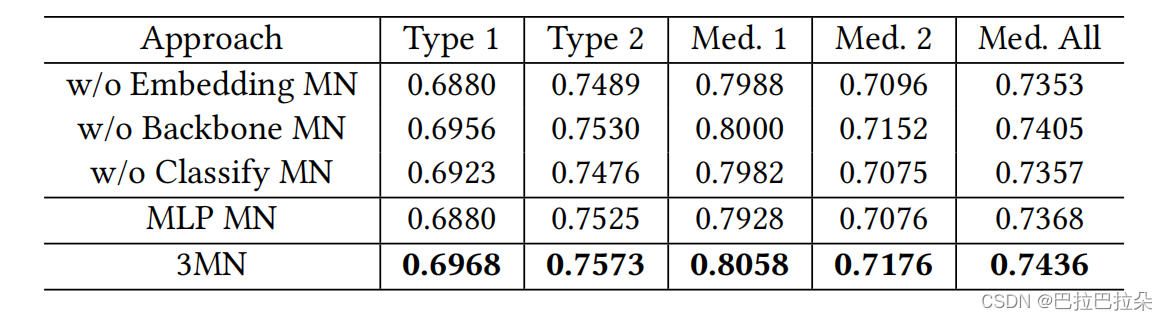
各个组件消融分析
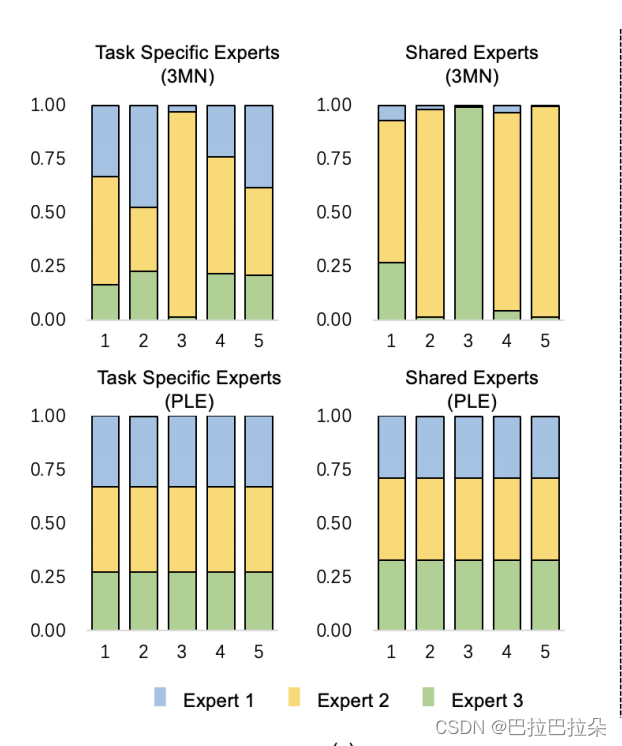
专家选择权重的可视化
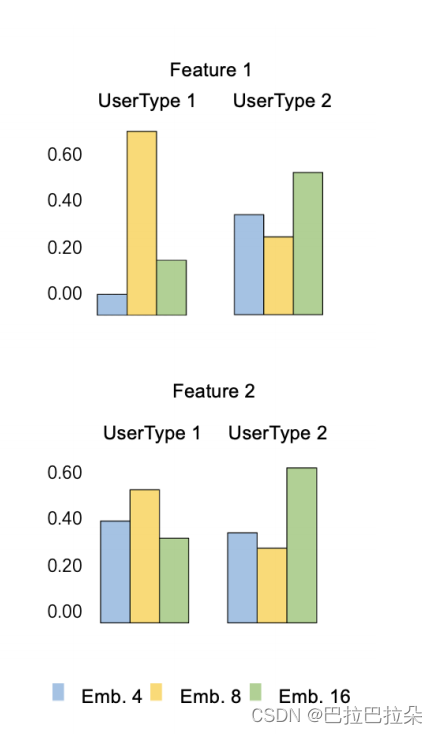
不同embedding尺寸选择权重的可视化
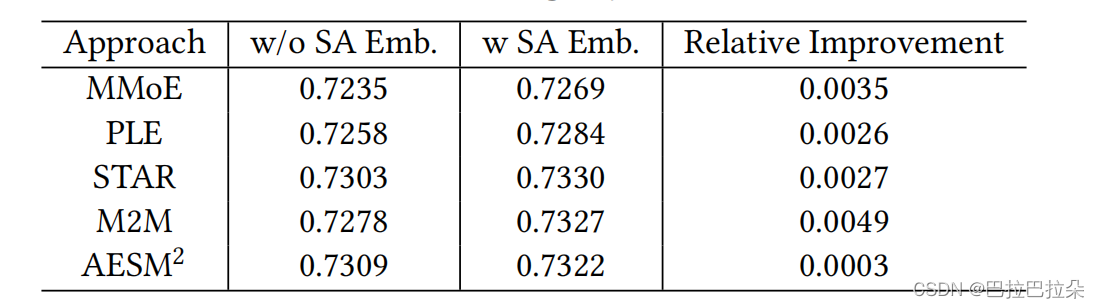
SA embedding layer加在base模型上的效果增益