1 GoogleNet Inception v2

v1具体结构：

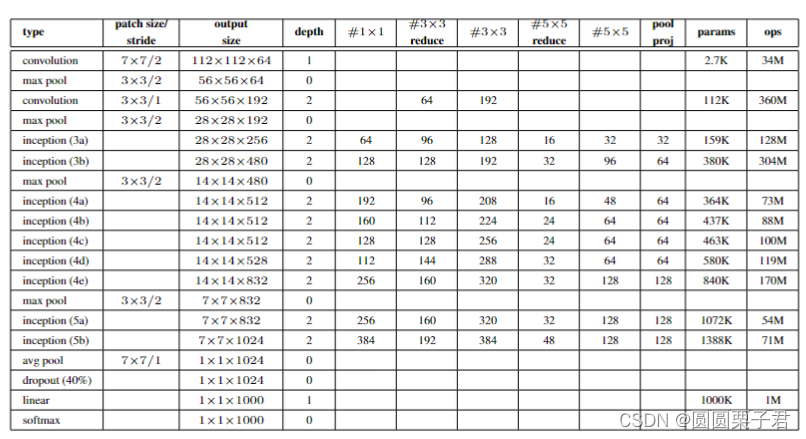
v2具体结构：

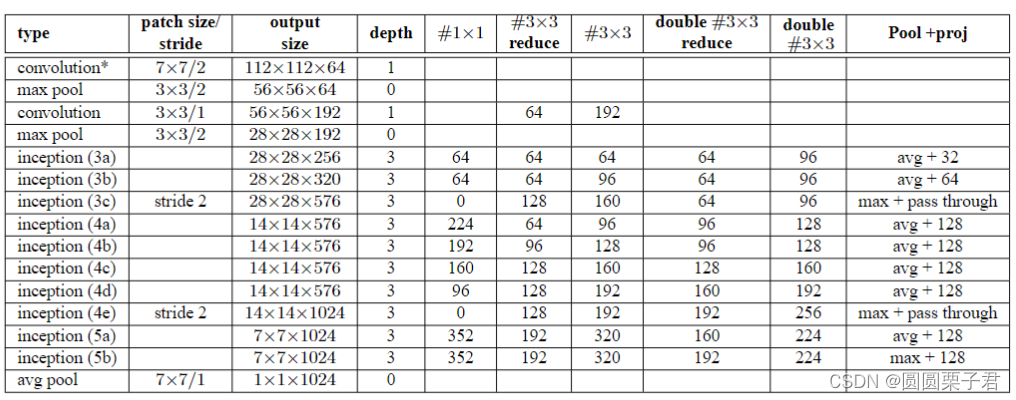
1 引入Batch Normalization（BN）:

Inception v2在每个卷积层之后引入了BN。这有助于解决深层网络中的梯度消失问题，同时加快训练过程并提高模型的收敛速度。BN通过减少内部协变量偏移，使每一层的输入更加稳定。

2 使用更小的卷积核:

Inception v2采用了更多的3x3卷积核代替大尺寸卷积核。这种设计可以减少参数数量，从而减少过拟合的风险，并降低计算复杂度。

Inception v2将大尺寸的卷积核（如5x5）分解成两个较小的卷积核（如3x3）。这不仅减少了参数的数量和计算量，还保持了网络的表达能力。如下图在v1中，只改变了，第三个位置的5x5变成了两个3x3，当然也修改了inception结构输出的通道数

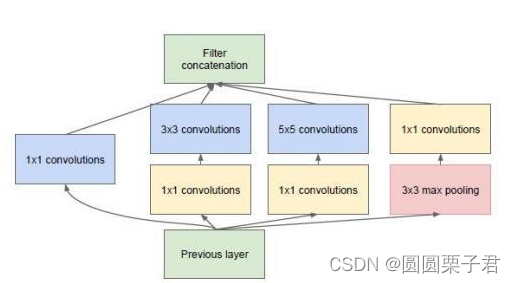
3 两处的maxpool替换成inception进行下采样

在inception3a和inception3b后面的池化层改成了inception3c进行下采样

inception3c参考上面2中的图来进行修改，去掉了第一个的1x1卷积，第二个为上图没有变化，步长变成2，第三个变成1x1，3x3，3x3的结构，就是把两个5x5分解成了两个3x3，最后一个卷积层步长为2，第四个删掉了1x1卷积，剩一个3x3的池化，步长也为2。只在inception3和inception4的池化就行修改，后面没有修改，还有删除了LRN，在每个卷积后面加上了BN

2 GoogleNet Inception v3

Inception v3实在inceptionv2的基础上做了改进

1 结构讲解

将7x7分解成三个3x3卷积，然后在inceptionv2中的第二次池化变成卷积进行下采样，即下图

然后对于第一类inception，就是inception3系列改成如下图

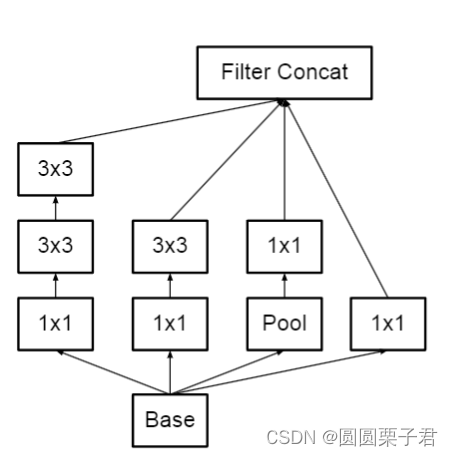
第二类inception改为下图

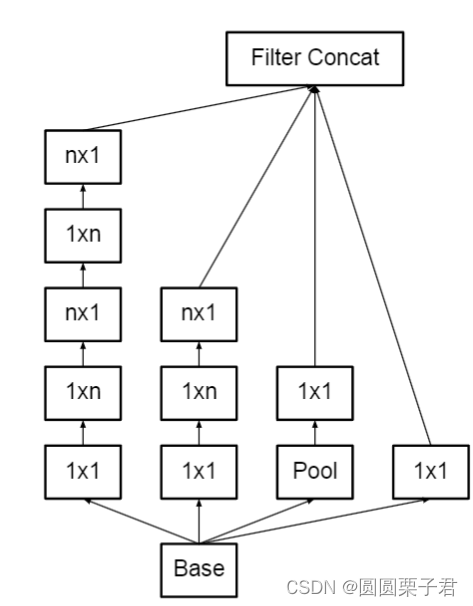
把一个1x1，两个3x3变成1x1,1x3,3x1,1x3,3x1，在感受野来说是差不多的，包括如下图理解

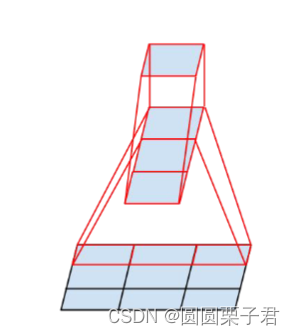
第三类inception改为下图

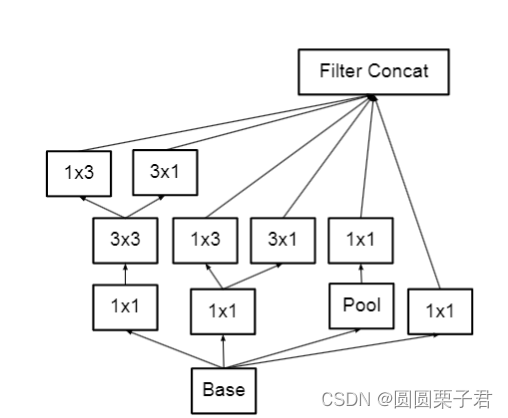
后面的话就没什么区别了，有人会想，为什么前面不用拆解，后面要拆解呢，对于前面浅层来说，提取的都是细节特征，如果进行拆解，则会导致效果不好，后面进行拆解，是因为后面提取的都是高度的抽象特征，拆解之后不仅可以减少计算量，还能增加特征的组合能力。

2 标签平滑

Inception v3在训练过程中采用了标签平滑技术，以降低模型过于自信的风险，增加模型的泛化能力

标签平滑作为一种正则化策略，有其特定的好处，尤其是从长远来看，它可以提高模型的泛化能力。下面是标签平滑带来的一些潜在好处：

1. 防止过拟合: 标签平滑通过防止模型对训练数据中的某些样本过于自信来减轻过拟合。当模型被迫也考虑到非目标类别时，它变得不那么确定，这有助于模型学习更加平滑、更具泛化能力的特征。

2. 提高模型的泛化能力: 通过避免模型完全信任训练数据中的标签，标签平滑鼓励模型在决策边界附近更加谨慎，这通常会导致更好的泛化性能。

3. 处理标签噪声: 在实际应用中，数据集可能包含错误或不确定性标签。标签平滑自然地给予模型一定的容忍度来处理这些不完美的标签。

4. 鼓励特征学习: 由于模型不能完全依赖标签，它必须通过学习更加鲁棒的特征表示来提高其预测的准确性。这可以导致模型在特征空间中更有效地学习区分不同类别。

虽然标签平滑可能会使得训练过程中的损失略微增加，但这种策略提供了更加稳健的模型学习方法，特别是在复杂的模型和大规模数据集上，它可以提高模型的最终性能。当然，像任何正则化技术一样，标签平滑的效果可能依赖于具体任务和数据集，因此实践中通常需要通过交叉验证来确定最佳的平滑参数 ϵ。