PTA | 1003 Emergency
书接上回,上次我们使用了python实现无向带权图与DFS算法的设计,本次我们将使用C++对本题进行解答,思路和题目分析同上一节内容,本次我们将在上一节的基础上继续实现。
okok现在又是激动人心的手搓代码时间:(代码思路来自哔哩哔哩)
首先,定义以下全局变量:
1, int N, M, C1, C2; 输入变量:城市数量,道路数量,起始城市, 终点城市
2, int path, teams; path表示路径数量,teams表示经过每个城市的最多的队伍数量
3, int num_of_team[500] = {0};表示每个城市的队伍数
4, int distence[500][500];距离矩阵
5, int mindis[500];最短路径数量
6, vector<int> v[500];用于构建无向带权图网络
此后,根据题意对输入数据进行处理:
int i,j,k,l; // j,k,l分别表示输入的两个城市j、k和这两者之间的距离l
cin >> N >> M >> C1 >> C2;
for(int i = 0; i < N; i ++){
cin >> num_of_team[i];
}
for(int i = 0; i < M; i++){
cin >> j >> k >> l;
// 无向带权图,则j—>k与k->j应当看作同一条路径,即二者作为端点均需要相互连接
v[j].push_back(k);
v[k].push_back(j);
// 距离矩阵中,二者之间的距离是一致的
distence[j][k] = distence[k][j] = l;
}此后,我们定义最短距离矩阵,为每个元素初始化为一个很大的数,表示两两之间并不相通:
for(int i=0; i<N; i++)mindis[i] = 100000000;重点来了,现在我们设计dfs函数:选择当前城市,当前走过的路径长度,当前积累的救援队数量作为传入参数,
void dfs(int curcity, int curlen, int curnums)第一步:剪枝
根据传入参数,我们可以意识到,当当前走过的路径长度curlen大于mindis[curcity],即并非第一次到达curcity且走过的路径长度比之前到达curcity所花费的距离大,直接return,
此后,由于我们的传入参数中并没有目标城市,因此对于当前城市,我们需要先对其进行判断:
if 是目标城市:
当前所走过的路径curlen是否小于该城市之前的所记录的最短距离mindis[city]:
if 距离相等:
说明是满足要求的最短路径之一,path自增1
同时比较当前积累的救援队数量curnums和最大救援队数量teams是否需要交换
elif 当前走过的路径curlen小于该城市之前的所记录的最短距离mindis[city]:
表示之前所有的路径均非最短路径,此时将重新对最短路径数组mindis[C2],路径数path,最大救援队数量teams重新赋值,
elif 非目标城市:
此时运用一点贪心的思想,比较当前走过的路程curlen与当前城市记录到的最短路径值,
if curlen < mindis[curcity]:
表示以前走过的到达本城市的路径均非最短路径,直接对其重新赋值为当前路径长度
for 对于所有与当前城市接壤的所有城市v[curcity]进行遍历,
将其中的所有城市与当前城市相结合,即在当前城市的基础上, 继续DFS,直到路径到达终点或者遍历结束
本部分较为繁琐, DFS的代码思路如上, 接下来是本部分的代码:
if(curcity == C2){ // if 是目标城市:
// 当前所走过的路径curlen是否小于该城市之前的所记录的最短距离mindis[city]:
// if 距离相等:
if(curlen == mindis[curcity]){
path ++;
if(curnums > teams){
teams = curnums;
}
}
// elif 当前所走过的路径curlen小于该城市之前的所记录的最短距离mindis[city]:
else{
mindis[C2] = curlen;
path = 1;
teams = curnums;
}
}
// elif 非目标城市:
else{
if(curlen < mindis[curcity])mindis[curcity] = curlen;
for(int i = 0;i < v[curcity].size(); i++){
// 在当前城市的基础上, 继续DFS,直到路径到达终点或者遍历结束
int j = v[curcity][i];
dfs(j, curlen+distence[curcity][j], curnums+num_of_team[j]);
}
}完整的代码如下:
#include<bits/stdc++.h>
using namespace std;
int N, M, C1, C2;
int path, teams;
int num_of_team[500] = {0};
int distence[500][500];
int mindis[500];
vector<int> v[500];
void dfs(int curcity, int curlen, int curnums){
if(curlen > mindis[curcity])return;
if(curcity == C2){
if(curlen == mindis[curcity]){
path ++;
if(curnums > teams){
teams = curnums;
}
}
else{
mindis[C2] = curlen;
path = 1;
teams = curnums;
}
}
else{
if(curlen < mindis[curcity])mindis[curcity] = curlen;
for(int i = 0;i < v[curcity].size(); i++){
int j = v[curcity][i];
dfs(j, curlen+distence[curcity][j], curnums+num_of_team[j]);
}
}
}
int main(){
int i,j,k,l;
cin >> N >> M >> C1 >> C2;
for(int i = 0; i < N; i ++){
cin >> num_of_team[i];
}
for(int i = 0; i < M; i++){
cin >> j >> k >> l;
v[j].push_back(k);
v[k].push_back(j);
distence[j][k] = distence[k][j] = l;
}
for(int i=0; i<N; i++)mindis[i] = 100000000;
dfs(C1, 0, num_of_team[C1]);
cout << path<< " " << teams;
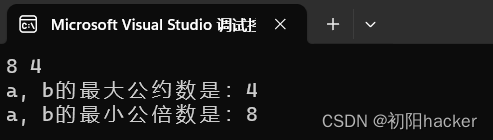
}以上就是使用C++解决本题的全部内容,最后附上AK截图:
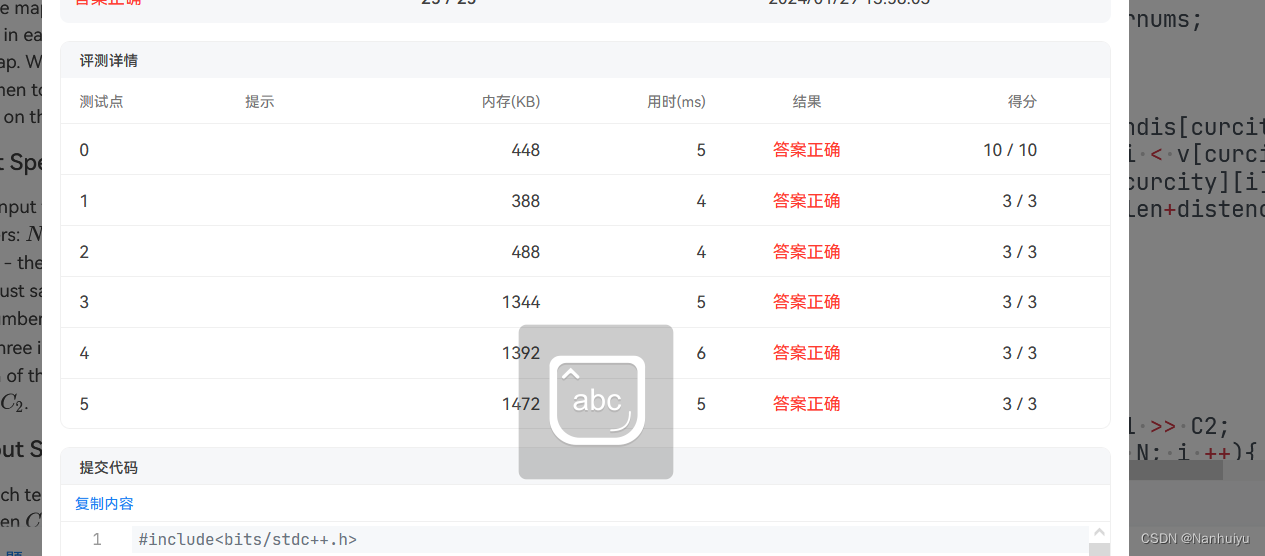
本题难度较大,思路尚未清晰的童鞋也不要气馁, 可以针对这部分内容多看看讲解或者是找一些简单题来练手, DFS题目重难点都在于DFS内容的设计,这部分没有固定的公式可以套用,但是只要思路清晰,虽然不能拿到全部的用例分,我相信大部分的分数还是可以拿到手的.
针对本题,C++部分的做法较为简单直接和常规,如果您有疑惑或者是更好的见解,请在评论区留言交流!