目录
介绍:
初始化:
建模:
预测:
改变结果:
介绍:
在深度学习中,神经元通常指的是人工神经元(或感知器),它是深度神经网络中的基本单元。深度学习的神经元模拟了生物神经元的工作原理,但在实现上更加简化和抽象。
在深度学习神经元中,每个神经元接收一组输入信号,通过加权求和和激活函数来生成输出信号。每个输入信号都有一个对应的权重,用于控制其对输出信号的影响程度。加权求和之后,通过激活函数进行非线性变换,以生成最终的输出信号。
参考: 使用程序设计流程图解析并建立神经网络(不依赖深度学习library)-CSDN博客 深度学习使用python建立最简单的神经元neuron-CSDN博客
初始化:
import numpy as np
from matplotlib import pyplot as plt
# (1) assign input values
input_value=np.array([[0,0],[0,1],[1,1],[1,0]])
input_value.shape
#结果:(4,2)
input_value
'''结果:
array([[0, 0],
[0, 1],
[1, 1],
[1, 0]])
'''
# (2) assign output values
output_value=np.array([0,1,1,0])
output_value=output_value.reshape(4,1)
output_value.shape
#结果:(4,1)
output_value
'''结果:
array([[0],
[1],
[1],
[0]])
'''
# (3) assign weights
weights = np.array([[0.3],[0.4]])
weights
'''结果:
array([[0.3],
[0.4]])
'''
# (4) add bias
bias = 0.5
# (5) activation function
def sigmoid_func(x):
return 1/(1+np.exp(-x))
# derivative of sigmoid function
def der(x):
return sigmoid_func(x)*(1-sigmoid_func(x))建模:
# updating weights and bias
j=0 #debug draw picture
k=[] #debug draw picture
l=[] #debug draw picture
for epochs in range(2000):
sum = np.dot(input_value, weights) + bias #summation and bias
act_output = sigmoid_func(sum) #activation
error = act_output - output_value #calculte error in predict
total_error = np.square(error).mean()
act_der = der(act_output) #Backpropagation and chain rule
derivative = error * act_der
final_derivative = np.dot(input_value.T, derivative)
j=j+1 #debug draw picture
k.append(j) #debug draw picture
l.append(total_error) #debug draw picture
print(j,total_error) #debug draw picture
# update weights by gradient descent algorithm
weights = weights - 0.5 * final_derivative
# update bias
for i in derivative:
bias = bias - 0.5 * i
plt.plot(k,l)
print('weights:',weights)
print('bias:',bias)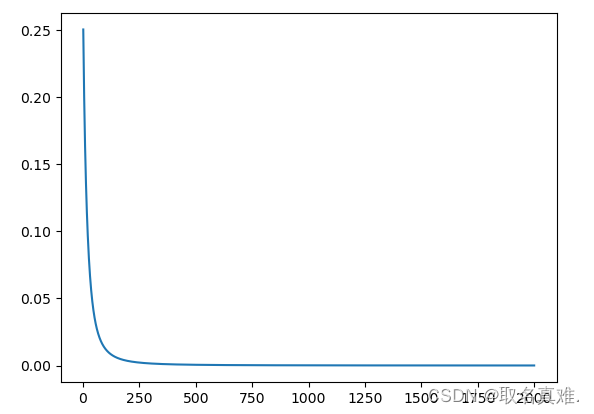
预测:
# prediction
pred = np.array([1,0])
result = np.dot(pred, weights) + bias
res = sigmoid_func(result) >= 1/2
print(res)
#结果:[False]改变结果:
output_value=np.array([0,1,1,0])
#改为
output_value=np.array([0,0,0,0])# updating weights and bias
j=0 #debug draw picture
k=[] #debug draw picture
l=[] #debug draw picture
for epochs in range(2000):
sum = np.dot(input_value, weights) + bias #summation and bias
act_output = sigmoid_func(sum) #activation
error = act_output - output_value #calculte error in predict
total_error = np.square(error).mean()
act_der = der(act_output) #Backpropagation and chain rule
derivative = error * act_der
final_derivative = np.dot(input_value.T, derivative)
j=j+1 #debug draw picture
k.append(j) #debug draw picture
l.append(total_error) #debug draw picture
print(j,total_error) #debug draw picture
# update weights by gradient descent algorithm
weights = weights - 0.5 * final_derivative
# update bias
for i in derivative:
bias = bias - 0.5 * i
plt.plot(k,l)
print('weights:',weights)
print('bias:',bias)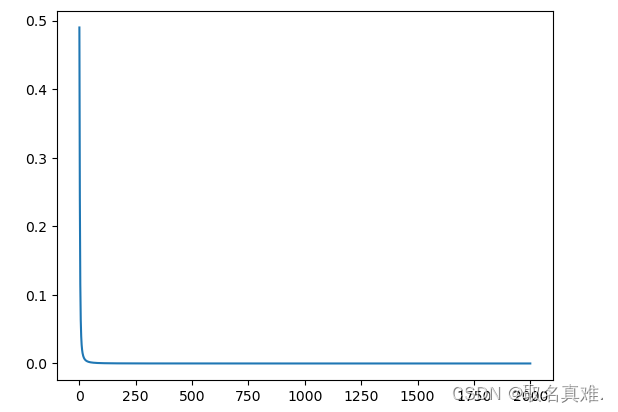
# prediction
pred = np.array([1,0])
result = np.dot(pred, weights) + bias
res = sigmoid_func(result) >= 1/2
print(res)
#结果:[False]