【基础算法练习】单调队列与单调栈模板

news2024/12/27 12:07:05

文章目录

单调栈
- 模板题
- 代码模板
- 算法思想
单调队列
- 模板题
- 代码模板
- 算法思想

单调栈

模板题

题目链接：ACwing 830. 单调栈

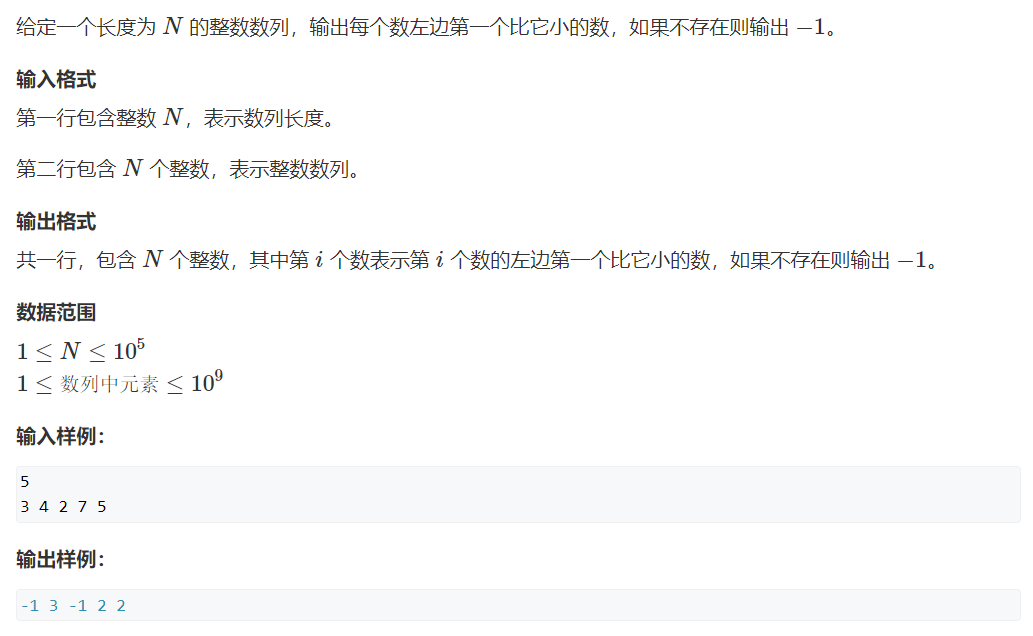
代码模板

#include <iostream>
#include <vector>
#include <stack>

using namespace std;

const int N = 100010;

vector<int> v(N);

int main()
{
    int n;
    cin >> n;
    stack<int> st;
    for (int i = 0; i < n; i++) cin >> v[i];
    for (int i = 0; i < n; i++) {
    	// v[i] 是当前在遍历的数, v[i] 比栈里的数小就 pop, 直到在栈里找到比他大的数
        while (!st.empty() && st.top() >= v[i]) st.pop();  
        if (!st.empty()) cout << st.top() << " ";
        else cout << -1 << ' ';
        st.push(v[i]);
    }
    return 0;
}

算法思想

单调栈的核心就是根据题目的要求维护一个具有单调性的栈，核心代码：while (!st.empty() && st.top() >= v[i]) st.pop(); 通过这一段代码，在下一个数入栈之前，将不符合题目要求的单调性的栈元素全部出栈，从而做到每次入栈都能保持单调栈的单调性

这就是单调栈的核心的算法思想

单调队列

模板题

题目链接：154. 滑动窗口

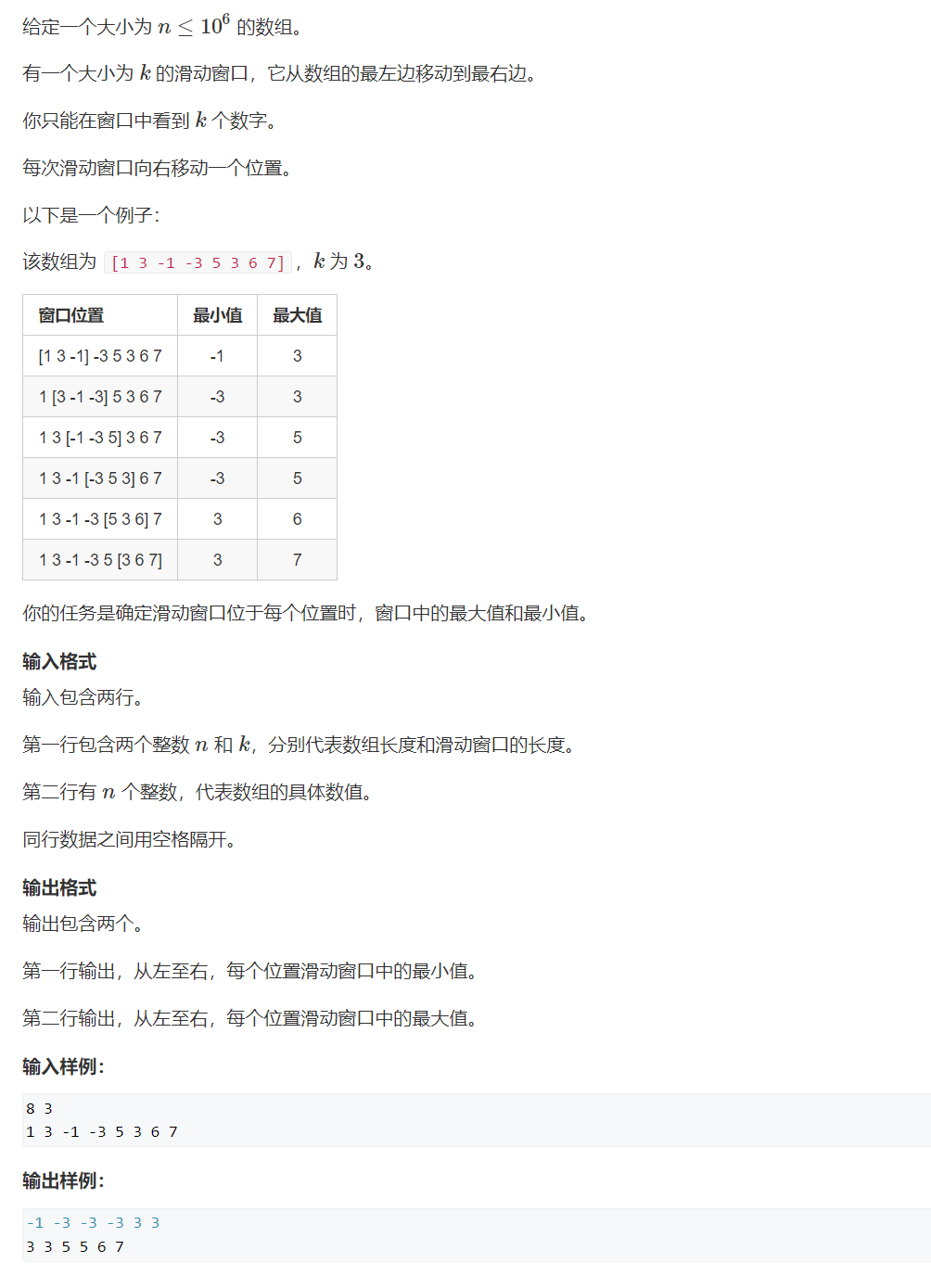
代码模板

#include <iostream>
#include <vector>
#include <deque>
using namespace std;

const int N = 1000010;

vector<int> v(N);

deque<int> q;

int main()
{
    int n, k;
    cin >> n >> k;
    for (int i = 0; i < n; i++) cin >> v[i];
    
    for (int i = 0; i < n; i++) { // 求最小值
        while (q.size() > 0 && q.back() > v[i]) q.pop_back(); // 比下一个数大的数全部都出队
        q.push_back(v[i]); // 入队
        if (i - k >= 0 && q.front() == v[i - k]) q.pop_front(); // 如果这个数在窗口到期了, 就出队
        if (i >= k - 1) cout << q.front() << " ";
    }
    
    q.clear();
    cout << endl;
    
    for (int i = 0; i < n; i++) { // 求最大值
        while (q.size() > 0 && q.back() < v[i]) q.pop_back(); // 比下一个数小的数全部都出队
        q.push_back(v[i]); // 入队
        if (i - k >= 0 && q.front() == v[i - k]) q.pop_front(); // 如果这个数在窗口到期了, 就出队
        if (i >= k - 1) cout << q.front() << " ";
    }
    return 0;
}