目录
BFS思路
可能需要看的视频和博客
代码如下
输出最短路径途径点

关于这种类型的题,我是有点印象的。。。当时蓝桥杯校内选拔就有这种题,当时还没学算法hhh
BFS思路
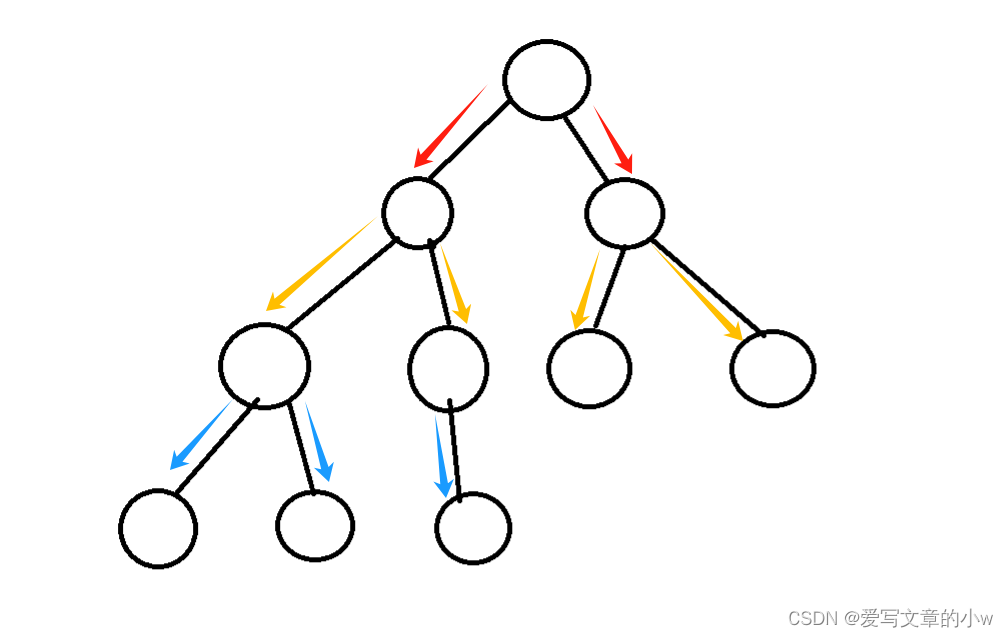
对应上图来理解BFS的方式还是很容易的,只是如何在题目中应用BFS的思想来解决问题呢?从具体的树的模型框架来看还容易理解,可是如果到了题目中这种二维数组走迷宫的形式,又该如何将我们已经理解的BFS思想对应到这种题目里面呢?
在走迷宫问题中,
我们可以将每一个可能的步骤或者位置看作是树的一个节点,因为我们每移动一个位置,都会距起始位置远一点,每到一个新的位置,就相当于到达了树的新的一层。
如果有多个具有相同地位的满足条件的位置,这些位置就可以看做是同一层的节点。
起始位置是根节点。每一次移动都相当于从当前节点到达子节点。
通过上面的叙述相信对这种方法的实际应用有了大概的思路。
可能需要看的视频和博客
下面这两个视频里有详细的走迷宫问题的广度优先搜索的动态过程,非常推荐看一下,会对BFS在迷宫问题里与在树的结构 之间的联系有更清晰的理解。
【【信息学奥赛教程】广度优先搜索算法 - 走迷宫】
【【直观的算法】如何用最短的路径走出迷宫】
我们这里用到数组模拟队列,需要回顾的可以看之前写的这篇文章
【第十一课】数组模拟栈和队列 / 单调栈 / 单调队列(滑动窗口) (c++代码 / 思路 )(acwing-828,829,830,154)
其实用数组模拟栈和队列甚至链表,其实主要就是运用数组的结构,但是更改数组下标的含义,这样的思路来模拟的。
代码如下
#include<iostream>
#include<cstring>//memset函数的头文件
using namespace std;
typedef pair<int,int> PII;//定义 坐标对
const int N=110;
int n,m;
int g[N][N];//存储二维迷宫
int d[N][N];//存储从起点到达 每个被访问过的位置 的最短路径长度
PII q[N*N];//创建N*N大小的队列,足以容纳整个迷宫的每个位置
int bfs()
{
int hh=0,tt=0;//定义队头和队尾
q[0]={0,0};//将起始点存入队列
memset(d,-1,sizeof d);//初始化迷宫所有的点为-1 表示未被访问过
d[0][0]=0;//起始点标记为0 表示已访问,并且起始点到(0,0) (也就是其自身)的最短路径长度为0
//表示在二维坐标系中,某点的四个相邻位置的 偏移量
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
while(hh<=tt)//只要队列中还有 待寻找下一个满足条件的节点 的当前节点时,就继续执行循环
{
PII t=q[hh++];//将队头元素出队
for(int i=0;i<4;i++)
{
//由于t是pair类型,可以由.first/.second访问元素(这里元素也就是x y坐标)
// 由原来的坐标加上偏移量就得出四个方向上的坐标
int x=t.first+dx[i];
int y=t.second+dy[i];
//首先要满足在迷宫大小范围内的可以通过的点(即g为0),并且未被访问过(保证了最短路)
if(x>=0 && x<n && y>=0 && y<m && g[x][y]==0 && d[x][y]==-1)
{
d[x][y]=d[t.first][t.second]+1;//更新最短路径长度
q[++tt]={x,y}; //将新位置加入队列
}
}
}
return d[n-1][m-1];//返回终点的最短路径长度
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
scanf("%d",&g[i][j]);
}
}
printf("%d",bfs());
return 0;
}很多需要解释的都写在注释里了。
我们在对这个迷宫进行广搜的时候,其实会遍历迷宫中的所有可以走的位置。因此可以说 d 数组是用来存储从起点到达二维网格中每个点所对应的最短路径长度。
我们是如何实现遍历所有可以走的位置呢?
在while循环内部,对每一个节点进行for循环遍历其周围的四个节点,如果有多种方向可选会发生什么?
上面的这两个问题其实互为对方的答案。
就是因为我们对每个方向都进行判断,或有多种可能的路径选择,才会将所有可以走的位置都遍历过,并且d数组的作用也可以用 “记录所有可行的点到起始点的最短距离”这一说法进行描述。
输出最短路径途径点
在前面代码基础上,做了一些添加。修改的的地方有注释。
#include<iostream>
#include<cstring>
using namespace std;
typedef pair<int,int> PII;
const int N=120;
int n,m;
int g[N][N],d[N][N];
PII q[N*N];
PII p[N][N];//记录前驱节点
int bfs()
{
int hh=0,tt=0;
q[0]={0,0};
memset(d,-1,sizeof d);
d[0][0]=0;
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
while(hh<=tt)
{
PII t=q[hh++];
for(int i=0;i<4;i++)
{
int x=t.first+dx[i];
int y=t.second+dy[i];
if(x>=0 && x<n && y>=0 && y<m && d[x][y]==-1 && g[x][y]==0)
{
d[x][y]=d[t.first][t.second]+1;
p[x][y]=t;//记录前驱节点,表明是从位置 t 移动到 (x, y) 的
q[++tt]={x,y};
}
}
}
//倒着输出最短路径的途径坐标点
int x=n-1,y=m-1;
while(x||y)
{
cout<<x<<" "<<y<<endl;
auto t=p[x][y];
x=t.first,y=t.second;
}
return d[n-1][m-1];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
scanf("%d",&g[i][j]);
}
}
cout<<bfs()<<endl;
return 0;
}这个不难理解,仔细想一下哦。
BFS先写到这。
有问题欢迎指出,一起加油!!