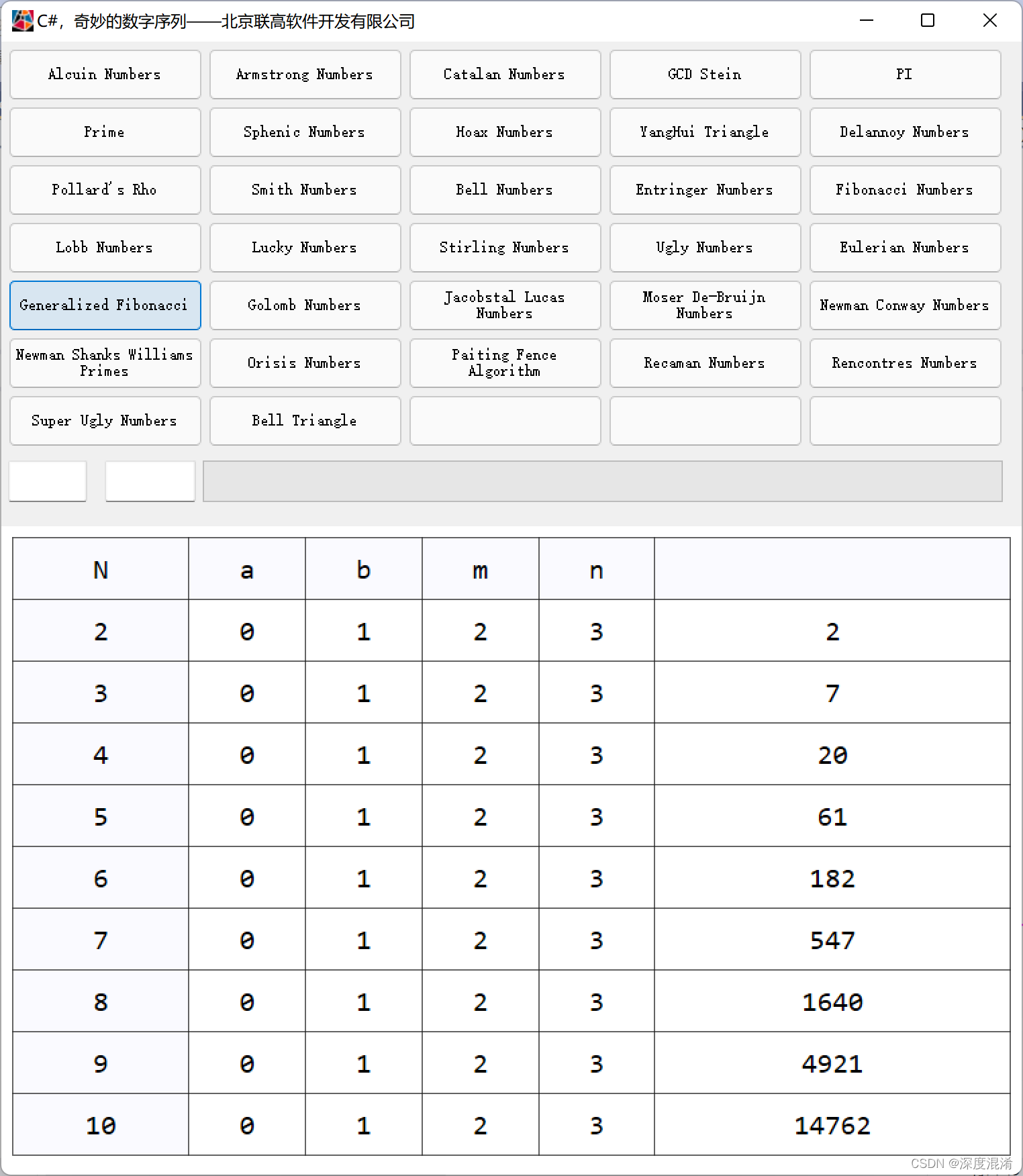
广义斐波那契序列(generalized Fibonacci sequence)是斐波那契数的推广。由递推关系F₁=F₂=…=Fm-1=0,Fₘ=1,Fm+n=Fₙ+Fn+1+…+Fn+m+1,n≥1所产生的序列,称为m级广义斐波那契序列。
计算结果:
源代码:
1 文本格式
using System;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// 广义斐波那契数
/// Generalised Fibonacci Numbers
/// </summary>
public static partial class Number_Sequence
{
/// <summary>
/// 广义斐波那契数的算法
/// </summary>
/// <param name="N"></param>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="m"></param>
/// <param name="n"></param>
/// <returns></returns>
public static int Generalized_Fibonacci_Number(int N, int a, int b, int m, int n)
{
int[,] F = { { m, 1 }, { n, 0 } };
if (N == 0)
{
return a;
}
if (N == 1)
{
return b;
}
if (N == 2)
{
return m * b + n * a;
}
int[,] initial = { { m * b + n * a, b }, { b, a } };
GFN_Power(ref F, N - 2, m, n);
Fib_Multiply(ref initial, F);
return F[0, 0];
}
/// <summary>
/// 2x2矩阵乘法
/// </summary>
/// <param name="F"></param>
/// <param name="M"></param>
static void Fib_Multiply(ref int[,] F, int[,] M)
{
int x = F[0, 0] * M[0, 0] + F[0, 1] * M[1, 0];
int y = F[0, 0] * M[0, 1] + F[0, 1] * M[1, 1];
int z = F[1, 0] * M[0, 0] + F[1, 1] * M[1, 0];
int w = F[1, 0] * M[0, 1] + F[1, 1] * M[1, 1];
F[0, 0] = x;
F[0, 1] = y;
F[1, 0] = z;
F[1, 1] = w;
}
private static void GFN_Power(ref int[,] F, int N, int m, int n)
{
int[,] M = { { m, 1 }, { n, 0 } };
for (int i = 1; i <= N; i++)
{
Fib_Multiply(ref F, M);
}
}
}
}
——————————————————
POWER BY TRUFFER.CN
2 代码格式
using System;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// 广义斐波那契数
/// Generalised Fibonacci Numbers
/// </summary>
public static partial class Number_Sequence
{
/// <summary>
/// 广义斐波那契数的算法
/// </summary>
/// <param name="N"></param>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="m"></param>
/// <param name="n"></param>
/// <returns></returns>
public static int Generalized_Fibonacci_Number(int N, int a, int b, int m, int n)
{
int[,] F = { { m, 1 }, { n, 0 } };
if (N == 0)
{
return a;
}
if (N == 1)
{
return b;
}
if (N == 2)
{
return m * b + n * a;
}
int[,] initial = { { m * b + n * a, b }, { b, a } };
GFN_Power(ref F, N - 2, m, n);
Fib_Multiply(ref initial, F);
return F[0, 0];
}
/// <summary>
/// 2x2矩阵乘法
/// </summary>
/// <param name="F"></param>
/// <param name="M"></param>
static void Fib_Multiply(ref int[,] F, int[,] M)
{
int x = F[0, 0] * M[0, 0] + F[0, 1] * M[1, 0];
int y = F[0, 0] * M[0, 1] + F[0, 1] * M[1, 1];
int z = F[1, 0] * M[0, 0] + F[1, 1] * M[1, 0];
int w = F[1, 0] * M[0, 1] + F[1, 1] * M[1, 1];
F[0, 0] = x;
F[0, 1] = y;
F[1, 0] = z;
F[1, 1] = w;
}
private static void GFN_Power(ref int[,] F, int N, int m, int n)
{
int[,] M = { { m, 1 }, { n, 0 } };
for (int i = 1; i <= N; i++)
{
Fib_Multiply(ref F, M);
}
}
}
}