01 背包
关键点
- 容器容量固定
- 每件物品只有两种状态:不选、选 1 件
- 求最大价值
代码
int N, W; // N件物品,容量为W
int w[N], v[N]; // w为大小,v为容量
/* 数组定义 */
int[][] dp = new int[N][W + 1]; // 注意是W + 1, 因为重量会取到W
dp[i][j]; // 从下标为[0, i]的物品中选若干件物品(注意是若干件,不是全部),放入大小为j的容器时的最大价值
/* 递推公式 */
// 由于每件物品有选、不选两种状态,所以两种状态取最大值即可
// 比如,对于dp[i][j]来说,
// 如果不选下标为i的物品,那么价值 = dp[i - 1][j];
// 如果选下标为i的物品,那么价值 = dp[i - 1][j - w[i]] + v[i]
// 两种状态取max
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
/* 初始化 */
// 从递推公式可以看出来,会存在dp[0][j]、dp[i][0]
// 对于dp[0][j]来说,回到数组定义,即选择下标为0的物品,放入大小为j的容器时的最大价值
// 这里又分两种情况,下标为0的物品的大小w[0]比j大,即放不进去,那么dp[0][j]=0;w[0]比j小,即放的进去,那么dp[0][j]=v[0]
// 对于dp[i][0]来说,回到数组定义,即从下标为[0, i]的物品中选若干件物品,放入大小为0的容器时的最大价值
// 显然dp[i][0] = 0
for(int i = 0; i < N; i ++ ) dp[i][0] = 0;
for(int j = 0; j <= W; j ++ ) {
if (j >= w[0]) dp[0][j] = v[0];
else dp[0][j] = 0;
}
/* 求解 */
// 先遍历物品、再遍历大小
// 由于dp[0]j]已经初始化过了,所以从第1件物品开始循环
// 由于dp[i][0]已经初始化过了,所以从重量为1开始循环
for(int i = 1; i < N; i ++ )
for(int j = 1; j <= W; j ++ ) {
if (j < w[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i];
}
/* 输出答案 */
// dp[N - 1][W]: 即从[0, N-1]中选若干件物品,放入大小为W的容器时的最大价值
return dp[N - 1][W];
时间复杂度:O(NW)
空间复杂度:O(NW)
优化:滚动数组,二维空间 -> 一维空间
递推公式
滚动数组思想:
回到递推公式:
d
p
[
i
]
[
j
]
=
M
a
t
h
.
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
−
1
]
[
j
−
w
[
i
]
]
+
v
[
i
]
)
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
dp[i][j]=Math.max(dp[i−1][j],dp[i−1][j−w[i]]+v[i])
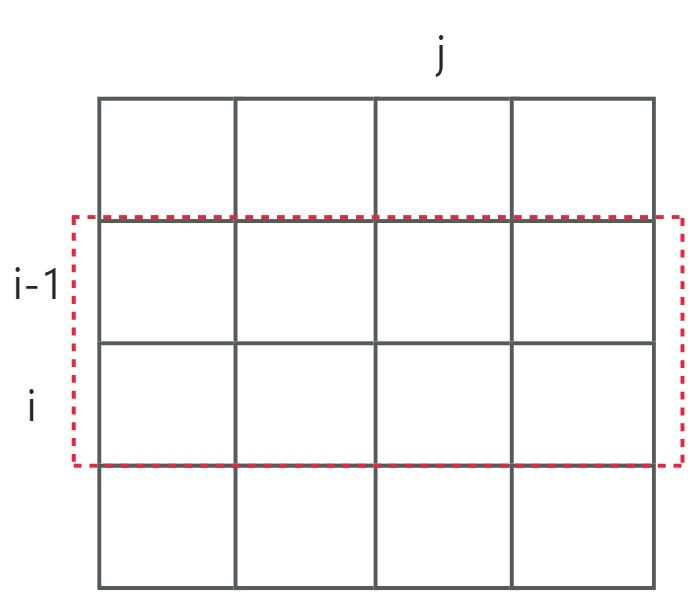
可以看出,第一维只用到了相邻两层的一个状态,没有第三个状态了。那实际上这个维度就可以去掉了,相当于用一个变量表示两个状态,赋值前就是上一层的状态,赋值后就是下一层的状态!
所以递推公式变成:
d
p
[
j
]
=
M
a
t
h
.
m
a
x
(
d
p
[
j
]
,
d
p
[
j
−
w
[
i
]
]
+
v
[
i
]
)
dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i])
dp[j]=Math.max(dp[j],dp[j−w[i]]+v[i])
容量 W 遍历方向
对于遍历方向也需要改。如下图所示:
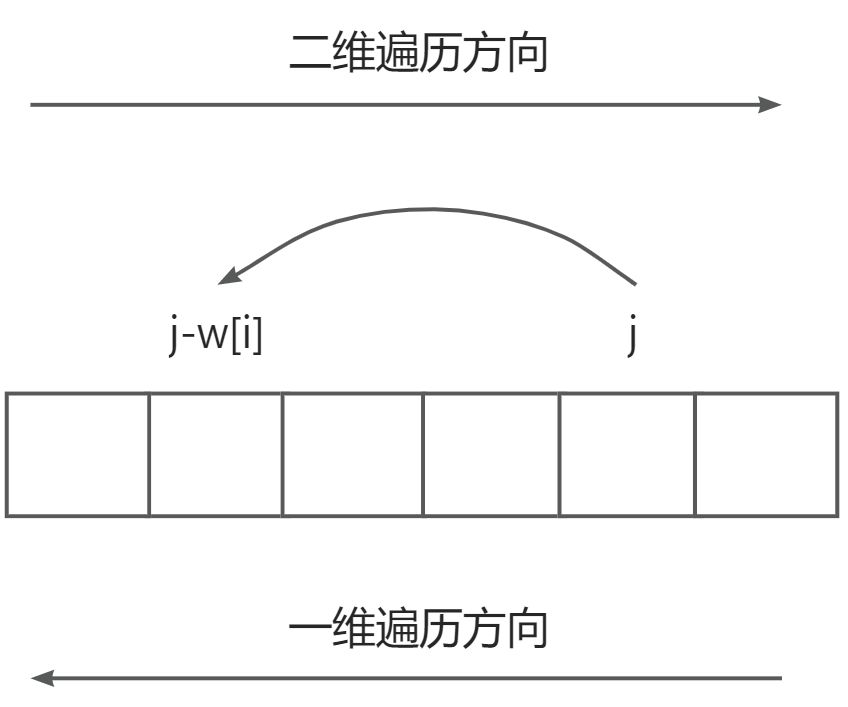
可以看出,后面的状态是用到了前面的状态的。如果还是像二维一样从左往右遍历的话,会出现这种情况:dp[j-w[i]] 被物品 i 更新了,dp[j] 也被物品 i 更新了。由于 dp[j] 是由 dp[j-w[i]] 更新过来的,相当于在重量为 j 的容器里放了两次物品 i,这和 01 背包的题目含义就冲突了:每件物品只有选和不选两种状态。
所以就要保证 dp[j] 用到的 dp[j-w[i]] 是没有被更新过的。方法也容易,反过来遍历就可以了。
初始化
一维的初始化实际上就是初始化一个物品都没用到时的价值。显然,对于任何重量的容器,不放物品,价值就是 0。初始化代码:
for(int j = 0; j <= W; j ++ ) dp[j] = 0;
容量 W 和物品 N 的遍历顺序
对于二维的形式,两种遍历方式都可以,因为不管怎么样,dp[i][j] 都是被左上角的状态更新的,所以先更新左上角的哪一个,实际上都一样。但是对于一维的形式,情况就不一样了。详细看一下两种方法的遍历的含义:
- 先遍历容量 W,再遍历物品 N:(×)
for(int j = W; j >=0; j -- )
for(int i = 0; i < N; i ++ ) {
if (j >= w[i]) dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
}
这种方法,相当于是对于同一个重量 j,从 N 个物品中选 1 个,看哪个价值最大。那最后 dp[W] 表示的就是从 N 个物品中选 1 个物品时的最大价值,这显然与 01 背包的题目含义冲突了:从 N 个物品中选若干个物品时(每个物品只选一次)的最大价值。
进一步分析,为什么这种方法每次都只会用到一个物品?因为每次递推用到的 dp[j-w[i]] 都是 0,因为 j 是从大到小遍历的,递推公式相当于变成了 dp[j]=Math.max(dp[j], v[i]),那不就是 N 个物品取最大值吗?所以也进一步加深了对一维递推公式的理解:要利用一维的递推,dp[j-w[i]] 一定要叠加了前面选了物品的状态。
- 先遍历物品 N,再遍历容量 W:(√)
for(int i = 0; i < N; i ++ )
for(int j = W; j >=0; j -- ) {
if (j >= w[i]) dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
}
这种方法,是先考虑前面物品的使用情况,放到 dp 中去,然后再开始考虑下一件物品。所以这种方法中,dp[j - w[i]] 是叠加了前面选了若干件物品之后的状态的。
因此,应该选择第二种遍历顺序。
时空复杂度
时间复杂度:O(NW)
空间复杂度:O(W),空间上比二维少了一个数量级
完整代码
int N, W; // N件物品,容量为W
int w[N], v[N]; // w为大小,v为容量
/* 数组定义 */
int[] dp = new int[W + 1]; // 注意是W + 1, 因为重量会取到W
dp[j]; // 大小为j的容器时的最大价值
/* 递推公式 */
dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
/* 初始化 */
for(int j = 0; j <= W; j ++ ) dp[j] = 0;
/* 求解 */
// 每迭代一次i,dp就多叠加了一件物品的状态
for(int i = 0; i < N; i ++ )
for(int j = W; j >= 0; j -- ) {
if (j >= w[i]) dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
}
/* 输出答案 */
// dp[W]: 大小为W的容器时的最大价值
return dp[W];
题目
https://kamacoder.com/problempage.php?pid=1046