[题目概述]

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式

第一行包含整数 N。
第二行包含 N 个整数，表示完整序列。

输出格式

输出一个整数，表示最大长度。

数据范围

$1\le N\le 1000，$
$-10^9\le 数列中的数\le 10^9$

输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

• 分析题意
  题目让我们求一串数字中的最大严格递增子序列的长度，不能是相等的，这题目最终落到了长度，也就是DP属性中的数量。
  注意： 这个子序列可以是跳的元素选的，不是必须挨着元素选。（我一开始就搞错了）
  先画个图
  
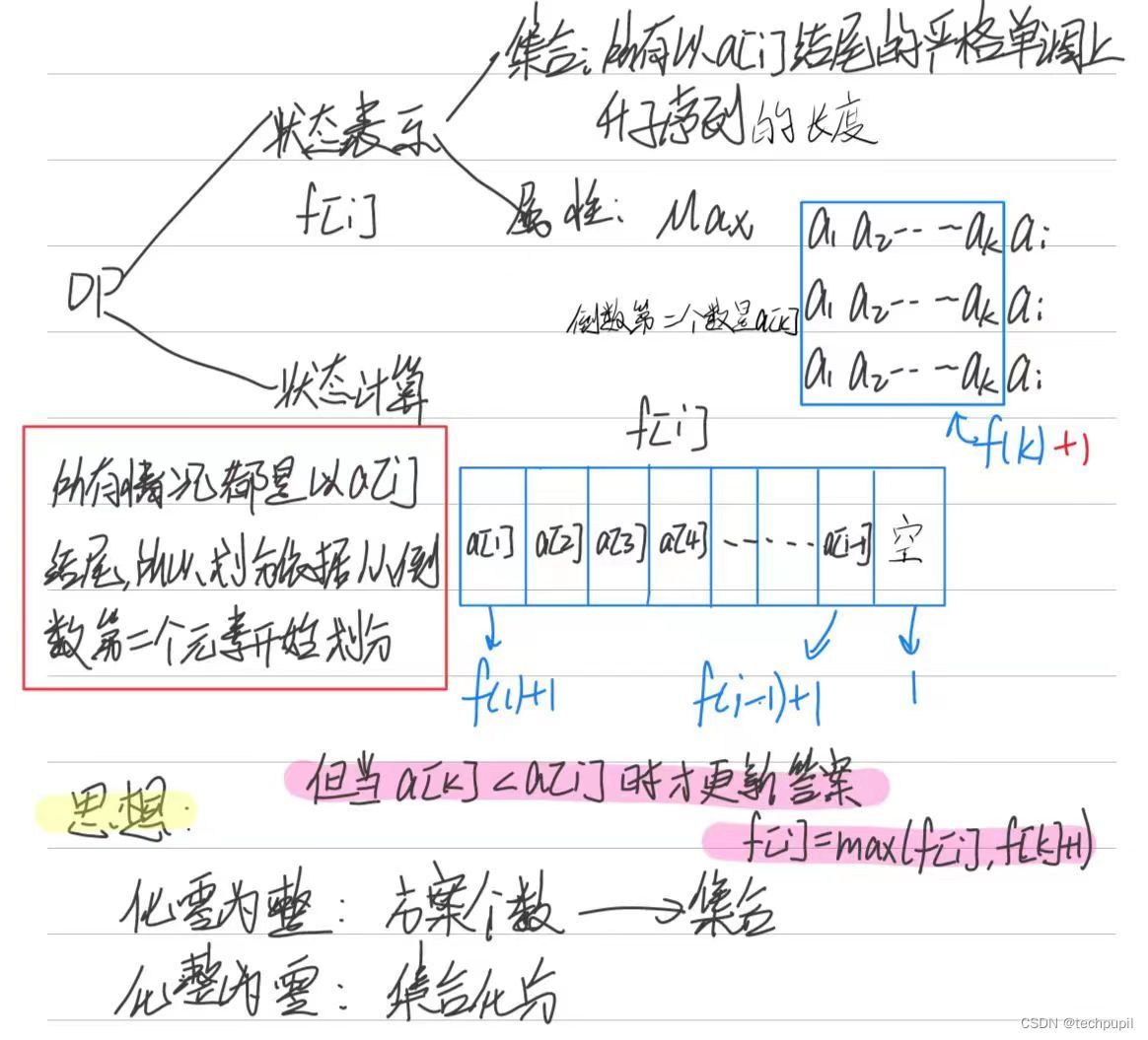
  划分条件是重点：要以第一个不同的元素开始划分，本题中所有序列的最后一个数都是a[i]，所以我们要从倒数第二个数入手。倒数第二个数范围就是$a[1]-a[i-1]$。那么此时就很好计算了。$f[i]=f[i-1]+1$。另外一种情况就是倒数第二个数为空，也就是整个序列只有一个数。
  这样代码就很好写了
• 完整代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 1010;
int n;

int a[N], f[N];

int main () {
	cin >> n;
	for (int i = 1; i <= n; i ++)
		cin >> a[i];

	for (int i = 1; i <= n; i ++) {
		f[i] = 1;
		for (int j = 1; j < i; j ++) {
			if (a[j] < a[i]) {
				f[i] = max(f[i], f[j] + 1);
			}
		}
	}

	int ret = 0;
	for (int i = 1; i <= n; i ++) {
		ret = max(ret, f[i]);
	}

	cout << ret << endl;
	return 0;
}

• 本题的分享就结束了，有问题的小伙伴可以发在评论区
  记得点赞关注加收藏！