国考省考行测:分析推理,形式逻辑
2022找工作是学历、能力和运气的超强结合体!
公务员特招重点就是专业技能,附带行测和申论,而常规国考省考最重要的还是申论和行测,所以大家认真准备吧,我讲一起屡屡申论和行测的重要知识点
遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开
测开的话,你就得学数据库,sql,oracle,尤其sql要学,当然,像很多金融企业、安全机构啥的,他们必须要用oracle数据库
这oracle比sql安全,强大多了,所以你需要学习,最重要的,你要是考网络警察公务员,这玩意你不会就别去报名了,耽误时间!
除了技术,申论和行测也得好好准备
文章目录
- 国考省考行测:分析推理,形式逻辑
- @[TOC](文章目录)
- 行测:所有,所有的,考察直言命题,集合推理
- 类型
- 所有a,都是b
- 所有a,都不是b
- 有的a,是b
- 有的a,不是b
- 某个a,是b,不是b
- 关系考察,重点,非常复杂
- 所有a,是b,矛盾一定是:有的a不是b
- 所有a,不是b,矛盾:有的a,是b
- 某个a,是b矛盾,某个a不是b
- 推出关系
- 所有a,是b——某个a是b——有的a是b
- 所有a不是b——某个a不是b——有的a不是b
- 反对关系
- 所有a是b,与所有a不是b:至少1假,可以俩都假【上反对】
- 有的a是b,与有的a不是b:至少1真,可以都是真【下反对】
- 考察场景:单考矛盾
- 考察场景:真假推理题中,综合考察
- 真假推理题,总结
- 解题方法:找,放,回
- 矛盾关系
- a——b矛盾是,肯前且否后,a且-b
- a且b矛盾是:-a或-b,a—— -b
- a或b矛盾是:-a且-b,a—— -b
- 要么a,要么b,矛盾是:全真,全假【a且b,-a且-b】
- 所有a是b,矛盾是,有的a不是b
- 所有a不是b,矛盾是:有的a是b
- 某个a是b,矛盾是:某个a不是b【某个a同一个对象】
- 必然a,矛盾是:不必然a,可能-a
- 必然-a,矛盾是:可能a
- 推出关系
- 反对关系
文章目录
- 国考省考行测:分析推理,形式逻辑
- @[TOC](文章目录)
- 行测:所有,所有的,考察直言命题,集合推理
- 类型
- 所有a,都是b
- 所有a,都不是b
- 有的a,是b
- 有的a,不是b
- 某个a,是b,不是b
- 关系考察,重点,非常复杂
- 所有a,是b,矛盾一定是:有的a不是b
- 所有a,不是b,矛盾:有的a,是b
- 某个a,是b矛盾,某个a不是b
- 推出关系
- 所有a,是b——某个a是b——有的a是b
- 所有a不是b——某个a不是b——有的a不是b
- 反对关系
- 所有a是b,与所有a不是b:至少1假,可以俩都假【上反对】
- 有的a是b,与有的a不是b:至少1真,可以都是真【下反对】
- 考察场景:单考矛盾
- 考察场景:真假推理题中,综合考察
- 真假推理题,总结
- 解题方法:找,放,回
- 矛盾关系
- a——b矛盾是,肯前且否后,a且-b
- a且b矛盾是:-a或-b,a—— -b
- a或b矛盾是:-a且-b,a—— -b
- 要么a,要么b,矛盾是:全真,全假【a且b,-a且-b】
- 所有a是b,矛盾是,有的a不是b
- 所有a不是b,矛盾是:有的a是b
- 某个a是b,矛盾是:某个a不是b【某个a同一个对象】
- 必然a,矛盾是:不必然a,可能-a
- 必然-a,矛盾是:可能a
- 推出关系
- 反对关系
行测:所有,所有的,考察直言命题,集合推理
定义:断定事务具有或不具有某种属性的命题
类型
所有a,都是b
集合具有b属性
所有a,都不是b
不具备b
有的a,是b
有的
有的a,不是b
某个a,是b,不是b
某个,那就是有一个?
全称肯定命题,否定命题,
特称肯定,否定命题
单称肯定,否定命题

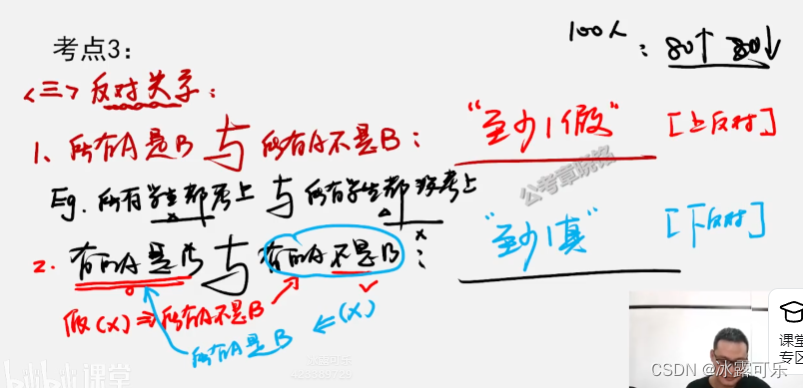
关系考察,重点,非常复杂
最爱考察:矛盾关系,非此即彼,一定不相容
所有a,是b,矛盾一定是:有的a不是b
eg
所有村民都能考上,矛盾:有的村民没考上
所有明星都偷税漏税,矛盾:有的明星没有偷税漏税
所有a,不是b,矛盾:有的a,是b
eg
所有学生都没迟到,矛盾:有的学生迟到了

某个a,是b矛盾,某个a不是b
easy
eg
王是狗,王不是狗
考得少
推出关系
所有a,是b——某个a是b——有的a是b
包含关系
eg
所有学生是党员——学生王是党员——有的学生是党员
6个箭头

所有a不是b——某个a不是b——有的a不是b
eg
所有演员都不爱国——演员范冰冰不爱国——有的演员不爱国

反对关系
所有a是b,与所有a不是b:至少1假,可以俩都假【上反对】
eg
所有学生都考上
所有学生都考不上
不能共存
不能同时成立,一定有一个假
至少一个假
有的a是b,与有的a不是b:至少1真,可以都是真【下反对】
能同时成立
有的学生是党员,有的不是党员
能同时不成立吗?
不能
矛盾关系
推出关系
反对关系

上反对和下反对知道上下了吧
考察场景:单考矛盾
eg
小明走丢了,所有人都不知道他下落
上述为假,则下面谁是真?
有的人知道啊
这就是矛盾关系考察
eg
所有人都讲究吃,有的人不讲究穿
前半句假,后半句是真,则:
有的人不讲究吃,有的人不讲究穿
对的

考察场景:真假推理题中,综合考察
eg
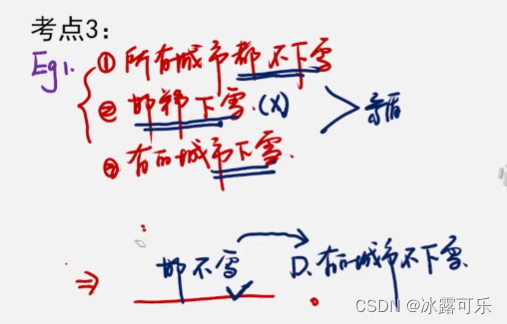
1所有城市都不下雪
2邯郸下雪
3有的城市下雪
只有1真,能得出?
2假
因为2可以推出3,2必然为假:邯郸不下雪——有的城市不下雪
13又是矛盾,真一定在13之间的,所以2必然假
eg
1所有城市都不下雪
2邯郸下雪
3有的城市下雪
4有的城市不下雪
上述只有2个真,2个假,则:
13矛盾,必有1真
24中必然有1真,具体是谁不知道
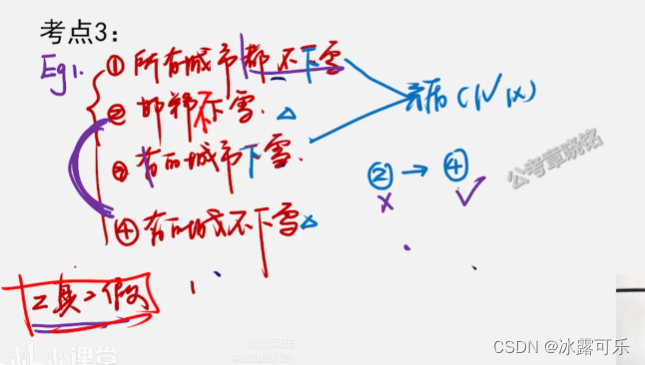
eg
1所有城市都不下雪
2邯郸不下雪
3有的城市下雪
4有的城市不下雪
上述只有2个真,2个假,则:
13矛盾,必然有1真
且24中必然有1真
因为2不下雪,能推出4,所以不能同时成立
于是乎2一定是假的,否则4就成立了
也就是说邯郸必须下雪
eg
1所有学生都考上
有的学生考上
有的学生没考上
学生王考上了
只有2真,则:
13矛盾,有真1
4可推出2,不行
所以王没考上
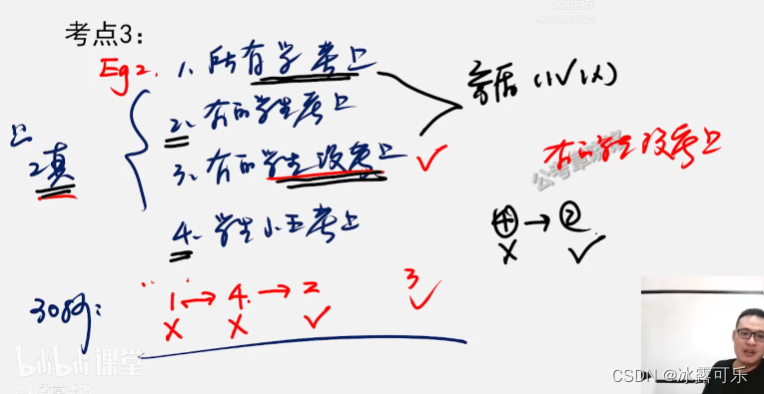
因为王没考上,所以3真
就1假
23真
OK了
eg
一个单位只有12人
1有人会用
2有人不会用
3所长不会
只有1真,则
3可以推出12,所以3不可能是真
所长会用
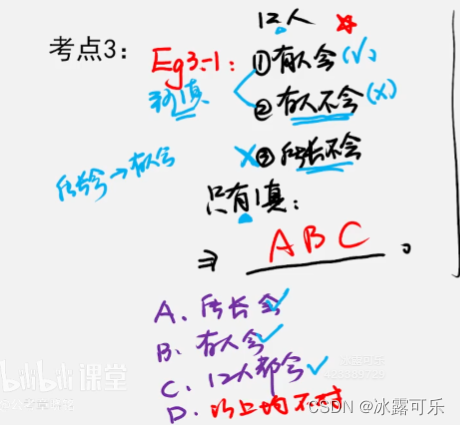
有的会,有的不会,至少一真

这个关系很骚
eg
一个单位只有12人
1所有人会用
2所有人不会用
3所长会
只有1假,则
只有一个假
因为12矛盾,必有1个假,所以3真
所长会,那么1真,2假
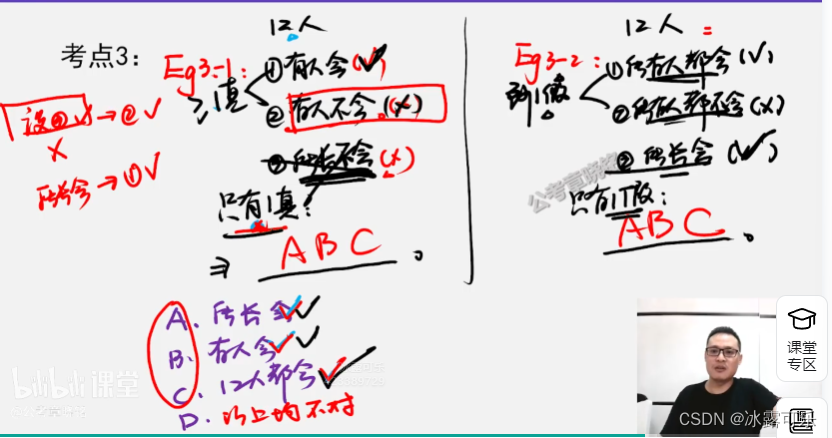
所以说:
有的人会,有的不会,那么至少1真
所与人会,所有人不会,至少1假
这是做题的技巧哦
真假推理题,总结
题目中给了几个条件,其中,有真有假,或者几个真几个假,据此推理:
解题方法:找,放,回
找到关系组:矛盾关系、推出关系、反对关系
放置关系组,看其他条件,判断真假
适当的回到关系组,判断真假

做题才会懂
矛盾关系
-号
a——b矛盾是,肯前且否后,a且-b
a且b矛盾是:-a或-b,a—— -b
a或b矛盾是:-a且-b,a—— -b
要么a,要么b,矛盾是:全真,全假【a且b,-a且-b】
所有a是b,矛盾是,有的a不是b
所有a不是b,矛盾是:有的a是b
某个a是b,矛盾是:某个a不是b【某个a同一个对象】
必然a,矛盾是:不必然a,可能-a

eg
明天必然下雪a
矛盾:明天可能不下雪,可能-a
必然-a,矛盾是:可能a
eg
必然考不上
矛盾:可能考上
推出关系

反对关系
2个所有,至少1假
2个有的,至少1真


13矛盾,必然有1真
所以24必然假
D就可以选了
13矛盾,但是没有办法推谁是真假