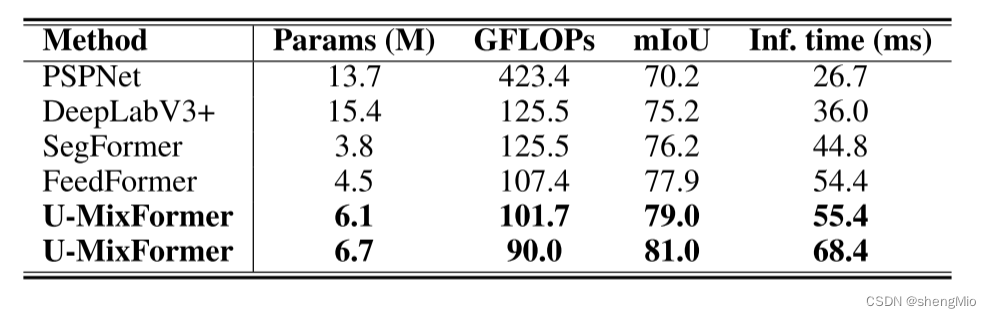
连通性判断

DFS连通性判断步骤：

1.从图上任意一点u开始遍历，标记u已经走过

2.递归u的所有符合连通条件的邻居点

3.递归结束，找到了的所有与u的连通点，就是一个连通块

4.然后重复这个步骤找到所有的连通块

BFS连通性判断步骤：

1.从图上任意一点u开始遍历，入队

2.弹出队首u，并且u已经被标记过，开始搜索u的邻居点放到队列中

3.弹出队首，重复步骤寻找连通点

题：全球变暖

你有一张某海域 ���NxN 像素的照片，"."表示海洋、"#"表示陆地，如下所示：

.......

.##....

.##....

....##.

..####.

...###.

.......

其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。

由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。

例如上图中的海域未来会变成如下样子：

.......

.......

.......

.......

....#..

.......

.......

请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入

第一行包含一个整数 N (1≤N≤1000)。

以下 �N 行 �N 列代表一张海域照片。

照片保证第 1 行、第 1 列、第 �N 行、第 �N 列的像素都是海洋。、

输出一个整数表示答案。

这道题，主要是通过找到第一个陆地，然后遍历整个岛屿，判断其中是否存在高低，如果有则这个岛屿就不会被淹没

1.DFS

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
char mp[N][N];
int vis[N][N];
int flag;
void dfs(int x,int y)
{
	vis[x][y]=1;
	int dir[4][2]={{0,-1},{0,1},{1,0},{-1,0}};
	if(mp[x][y]=='.')return;
	if (mp[x+1][y]=='#' && mp[x][y+1]=='#' && mp[x-1][y]=='#' && mp[x][y-1]=='#')flag=1;
	for (int i=0;i<4;++i)
	{
		int  tx=x+dir[i][0],ty=y+dir[i][1];
		if (vis[tx][ty]==0 && mp[tx][ty]=='#')
			dfs(tx,ty);
	}
}
int main()
{
	int n;
	cin>>n;
	for (int i=0;i<n;++i)
	{
		cin>>mp[i];
	}
	int ans=0;
	for (int i=0;i<n;++i)
	{
		for (int j=0;j<n;++j)
		{
      if (mp[i][j]=='#' && vis[i][j]==0)
			{flag=0;
      dfs(i,j);
      if (flag==0)ans++;}
		}
	}
	cout<<ans;
}

2.BFS

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
char mp[N][N],flag;
int vis[N][N];
void bfs(int x ,int y)
{
  queue<pair<int, int> > q;
  q.push({x,y});
  vis[x][y]=1;
  int dir[4][2]={{0,-1},{0,1},{1,0},{-1,0}};
  while (q.size())
  {
    pair<int,int>p;
    p=q.front();
    q.pop();
    int tx=p.first,ty=p.second;
    if (mp[tx+1][ty]=='#' && mp[tx][ty+1]=='#' && mp[tx-1][ty]=='#' && mp[tx][ty-1]=='#')flag=1;
    for (int i=0;i<4;++i)
    {
      int nx=tx+dir[i][0],ny=ty+dir[i][1];
      if (mp[nx][ny]=='#' && vis[nx][ny]==0)
      {
        vis[nx][ny]=1;
        q.push({nx,ny});
      }
    }
  }
}
int main()
{
  int n;
  cin>>n;
  int ans=0;
  for (int i=0;i<n;++i)cin>>mp[i];
  for (int i=0;i<n;++i)
  {
    for (int j=0;j<n;++j)
    {
      if (vis[i][j]==0 && mp[i][j]=='#')
      {
        
        bfs(i,j);
        if (flag==0)ans++;
        flag=0;
      }
    }
  }
  cout<<ans;
}

判重

由于DFS和BFS都是暴力的搜索方法，所以很容易超时，所以DFS需要剪枝，BFS需要判重

题：跳蚱蜢https://www.lanqiao.cn/problems/642/learning/?page=1&first_category_id=1&problem_id=642

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

如下图所示： 有 99 只盘子，排成 11 个圆圈。 其中 88 只盘子内装着 88 只蚱蜢，有一个是空盘。 我们把这些蚱蜢顺时针编号为 11 ~ 88。

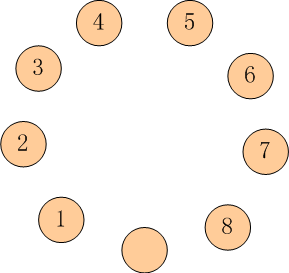
每只蚱蜢都可以跳到相邻的空盘中， 也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。

请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列， 并且保持空盘的位置不变（也就是 1−81−8 换位，2−72−7换位,...），至少要经过多少次跳跃？

这道题，就 引入了map来记录经过的字符串，下次在变成这个串的时候就可以直接跳过

#include <bits/stdc++.h>
using namespace std;
struct node{
	node(){}
	node(string ss,int tt){s=ss,step=tt;}
	string s;
	int step;
};
int cnt=0;
queue<node>q;
map<string,bool>mp;
void solve()
{
	while (!q.empty())
	{
		node now=q.front();
		q.pop();
		string s=now.s;
		int step=now.step;
		if (s=="087654321")
		{
			cout<<step<<endl;
			cout<<cnt<<endl;
			break;
		}
		int i;
		for (i=0;i<10;++i)
		{
			if (s[i]=='0')break;
		}
		for (int j=i-2;j<=i+2;++j)
		{
			int k=(j+9)%9;
			if (k==i)continue;
			string news=s;
			char temp=news[i];
			news[i]=news[k];
			news[k]=temp;
			cnt++;
			if (!mp[news])
			{
				mp[news]=true;
				q.push(node(news,step+1));
			}
		}
	}
}
int main()
{
	string s="012345678";
	q.push(node(s,0));
	mp[s]=true;
	solve();
}

剪枝

剪格子https://www.lanqiao.cn/problems/211/learning/?page=1&first_category_id=1&problem_id=211

题目描述

如下图所示，3 x 3 的格子中填写了一些整数。

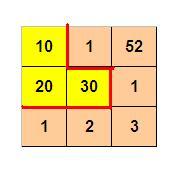
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 60。

本题的要求就是请你编程判定：对给定的 �×�m×n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 0。

输入描述

输入描述

程序先读入两个整数 �,�m,n 用空格分割 (�,�<10)(m,n<10)，表示表格的宽度和高度。

接下来是 �n 行，每行 �m 个正整数，用空格分开。每个整数不大于 104104。

输出描述

在所有解中，包含左上角的分割区可能包含的最小的格子数目。

这道题的思路很简单，就是找到所有格子总和的一半，所以当此时相加的总和超过一半的时候，就可以直接退出，达到剪枝的效果

#include <bits/stdc++.h>
using namespace std;
int a[11][11];
int m,n,sum,minx=100005;
int vis[11][11];
void dfs(int x,int y,int s,int l)
{
	if (s==sum/2 )
	{
		if (minx>l && vis[0][0])minx=l;
		return;	
	}
	if (s>sum/2)return;
	int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
	for (int i=0;i<4;++i)
	{
		int tx=x+dir[i][0],ty=y+dir[i][1];
		if (vis[tx][ty]==1 || tx<0 || ty<0 || tx>=m || ty>=n)continue;
		vis[tx][ty]=1;
		dfs(tx,ty,s+a[tx][ty],l+1);
		vis[tx][ty]=0;
	}
	return ;
}
int main()
{
	cin>>m>>n;
	for (int i=0;i<n;++i)
	{
		for(int j=0;j<m;++j)
		{
			cin>>a[i][j];
			sum+=a[i][j];
		}
	}
	vis[0][0]=1;
	dfs(0,0,a[0][0],1);
	cout<<(minx==100005?0:minx);
	return 0;
}