字符串的模式匹配
- 引言
- 应用
- 方法一 暴力匹配算法 (C语言实现)
- 程序实现
- 暴力算法思想
- 暴力算法的时间复杂度
- 方法二 KMP 算法
- 程序实现
- KMP 算法思想
- KMP 算法的时间复杂度
- 暴力匹配算法 vs KMP 算法
- next 数组的训练
- KMP 算法的优化
- next 数组 转换成 nextval 数组的思想
引言
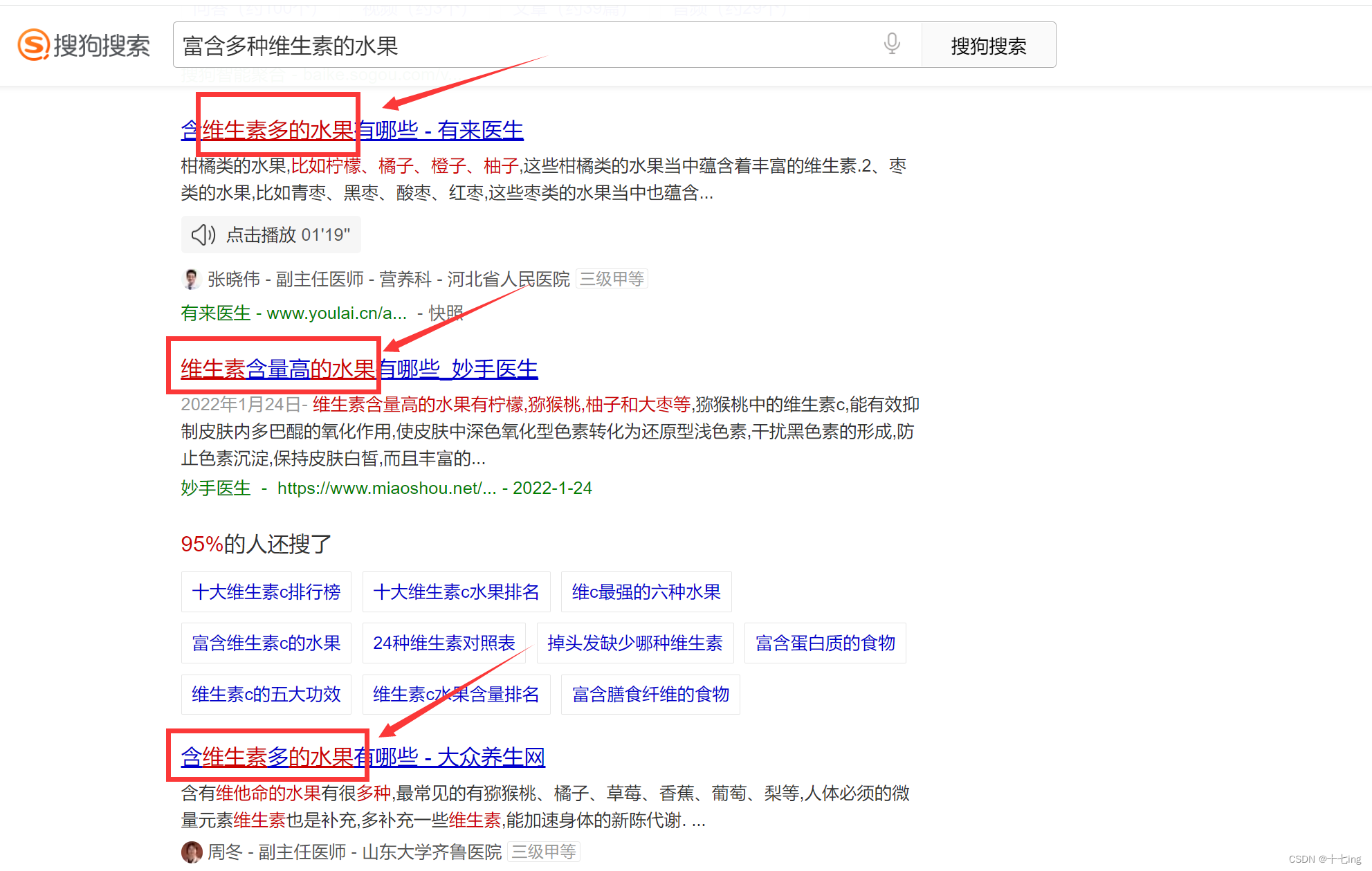
在我们日常生活中,需要从一个网站上搜索关键字,实际上网站会帮我们从数据库中寻找与这些关键字相匹配的句子或者一段话。
应用
对于上面的例子,一个完整的句子我们可以称其主串,输入的关键字我们可以称其模式串,在主串中匹配相同的关键字,我们可以说是在主串中找与模式串相同的子串。
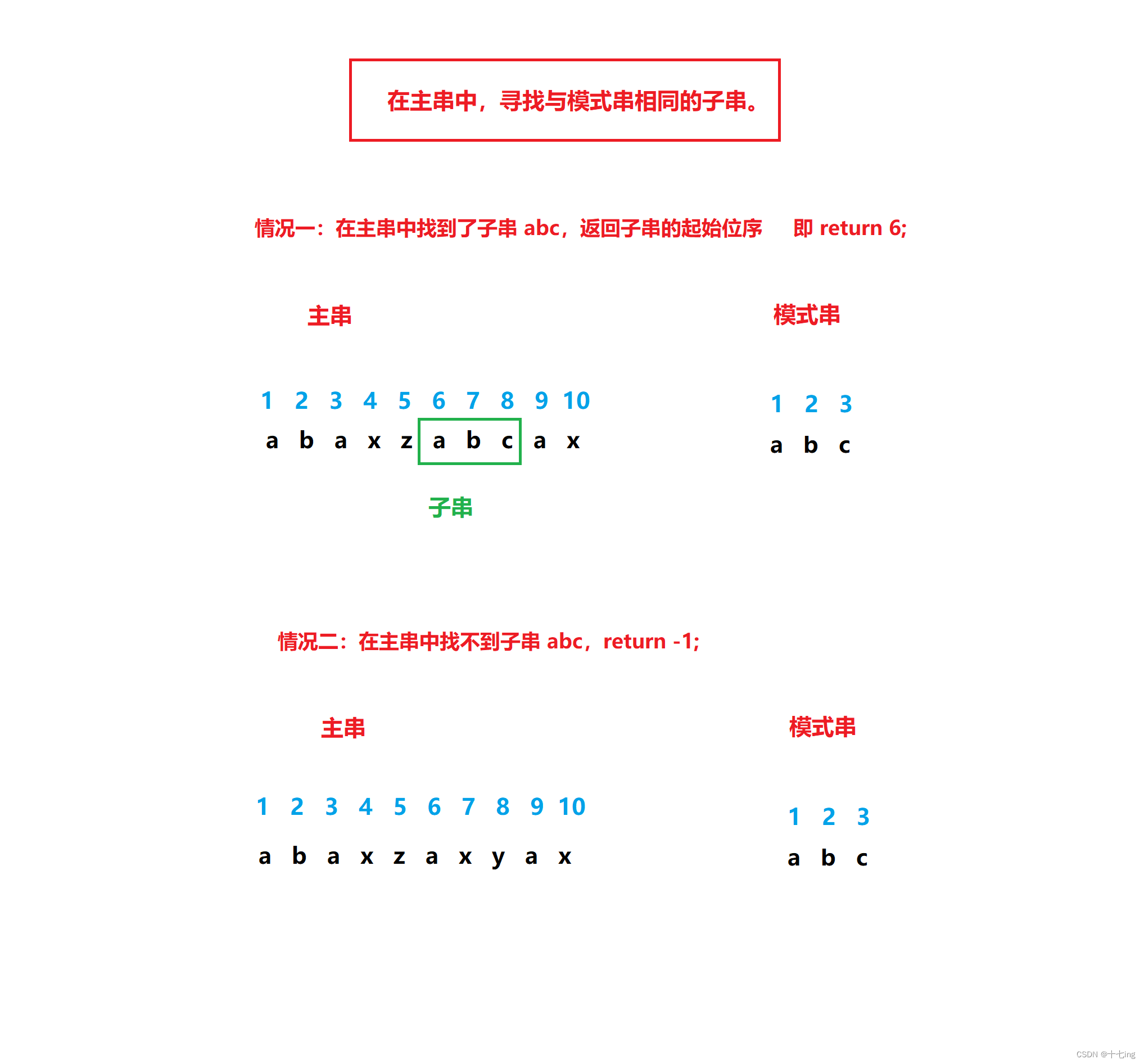
所以,这就是本篇博客所讨论的模式匹配:在主串中,寻找与模式串相同的子串,并返回子串的起始位置。举两个简单的例子,情况如下:
方法一 暴力匹配算法 (C语言实现)
程序实现
#include <stdio.h>
int find_substring(char arr1[], char arr2[], int len1, int len2) {
int i = 1;
int j = 1;
while (i <= len1 && j <= len2) {
if (arr1[i - 1] == arr2[j - 1]) {
i++;
j++;
}else {
i = i - j + 2;
j = 1;
}
}
// 跳出循环后,如果此刻的位置,j > len2,那么就是匹配成功
if (j > len2) {
return i - len2;
}
// 否则就是未找到模式串
return -1;
}
int main() {
char arr1[] = "abaxzabcax"; // 主串
char arr2[] = "abc"; // 模式串
int len1 = 10;
int len2 = 3;
int ret = find_substring(arr1, arr2, len1, len2);
printf("%d\n", ret);
return 0;
}
暴力算法思想
约定用 i 遍历主串序列,用 j 遍历模式串序列。
在主串中,从左往右扫描,每次以模式串的数量单位 (这里三个单位) 进行扫描,在扫描的过程中,拿每个字符和模式串对比。
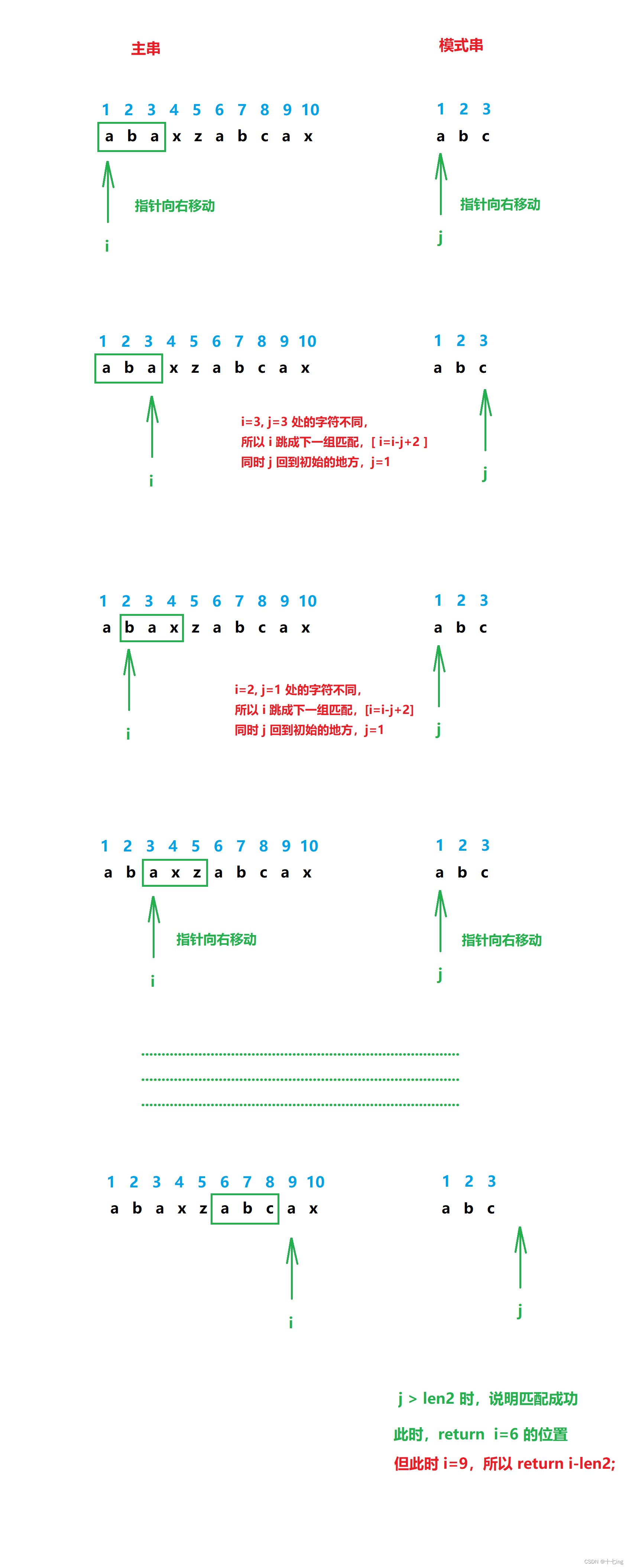
暴力算法的时间复杂度
最优的时间复杂度:O(1)
最坏的时间复杂度:O(nm)
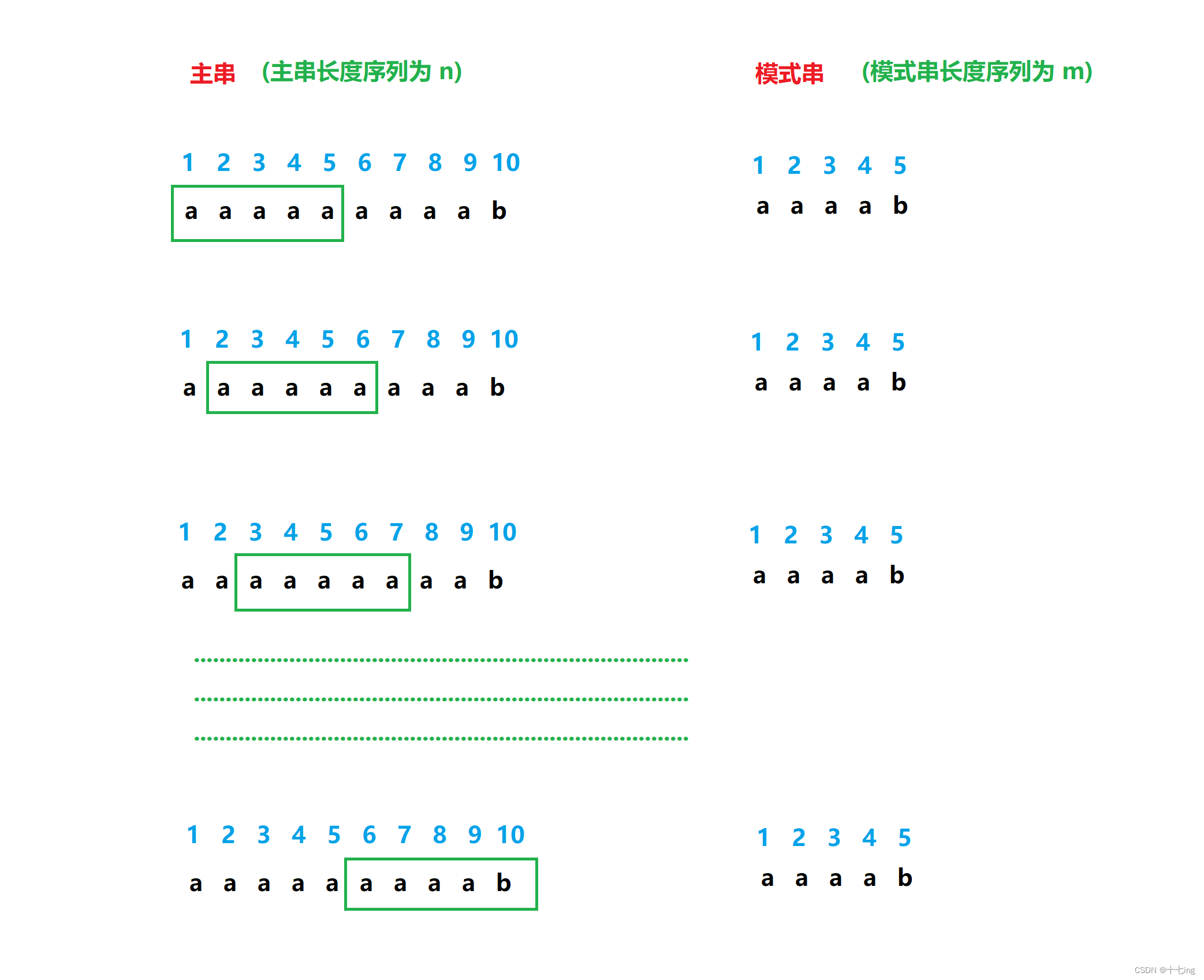
讨论最坏的情况:主串长度序列为 n,模式串长度序列为 m.
一般情况,主串长度大于模式串,那么我们在主串中寻找子串时,最坏情况下每次都要匹配 m 个元素,最多匹配 n-m+1 次,才能彻底匹配完。即 O( m * [n-m+1] ) ≈ O(nm).
方法二 KMP 算法
程序实现
#include <stdio.h>
int KMP_find_substring(char* arr1, char* arr2, int len1, int len2, int* next) {
int i = 1;
int j = 1;
while(i <= len1 && j <= len2){
if (j == 0 || arr1[i - 1] == arr2[j - 1]) {
i++;
j++;
}else {
j = next[j];
}
}
// 跳出循环后,如果此刻的位置,j > len2,那么就是匹配成功
if (j > len2) {
return i - len2;
}
// 否则就是未找到模式串
return -1;
}
int main() {
char arr1[] = "abaacaabcabaabc"; // 主串
char arr2[] = "abaabc"; // 模式串
int next[] = { 0,0,1,1,2,2,3 };
// 数组下标: 0 1 2 3 4 5 6
// 重置后的 j: / 0 1 1 2 2 3
int len1 = 15;
int len2 = 6;
int ret = KMP_find_substring(arr1, arr2, len1, len2, next);
printf("%d\n", ret);
return 0;
}
KMP 算法思想
约定用 i 遍历主串序列,用 j 遍历模式串序列。
① 根据模式串设计 next 数组,用来重置下一次 j 的位置。
② 根据 next 数组中的 j,来间断遍历主串序列,在使用 i 遍历主串序列时,整个过程不回溯。
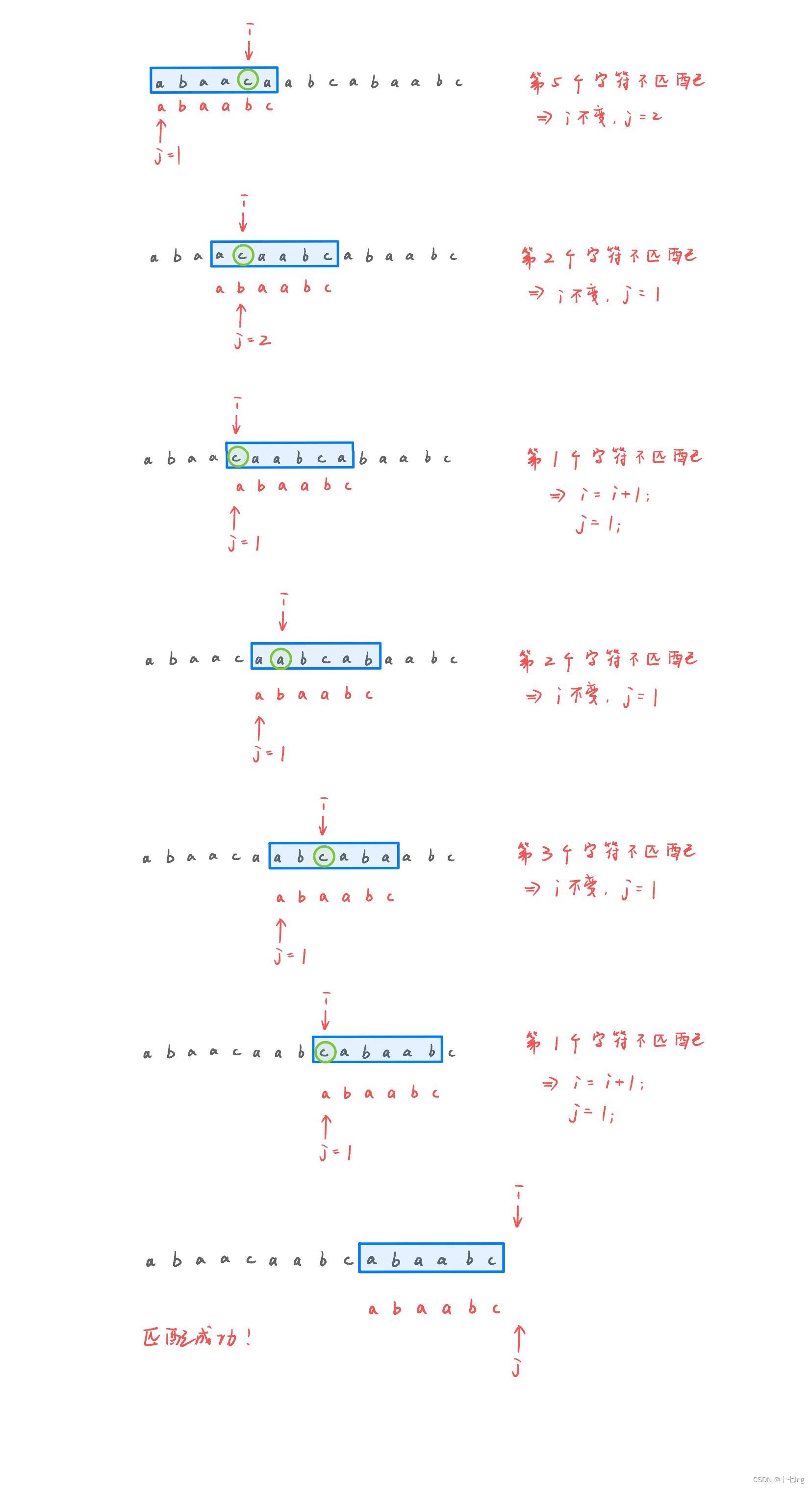
例如:对于模式串为 " abaabc" 的序列,求 next 数组。
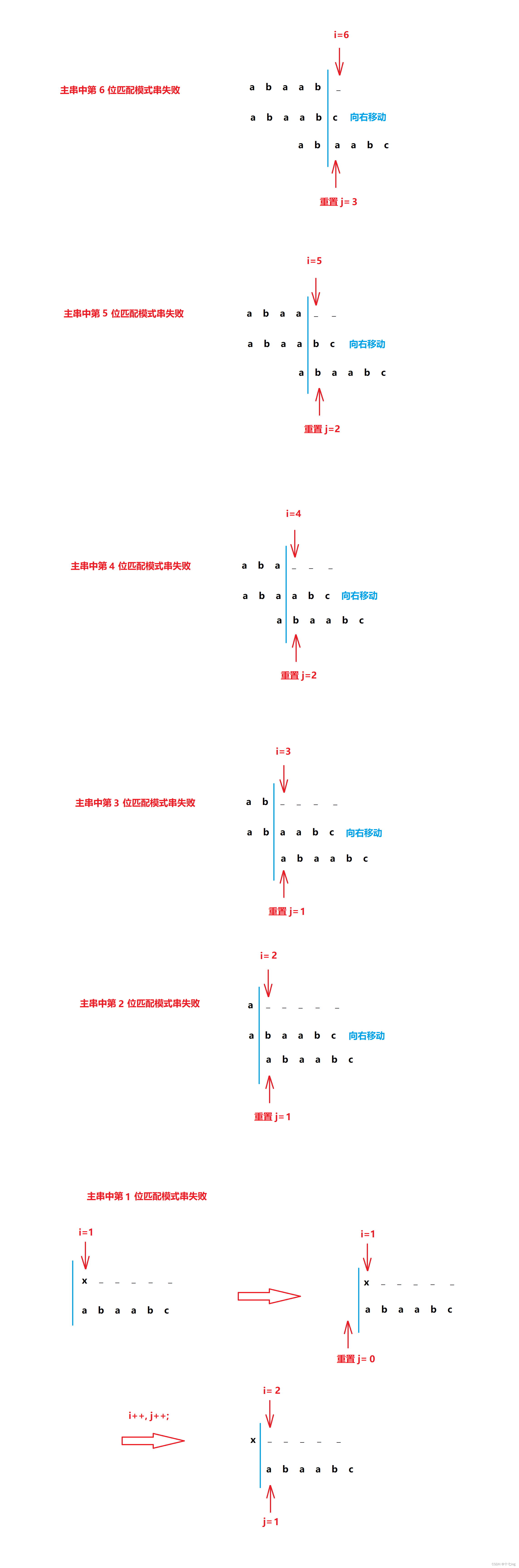
计算后的 next 数组:
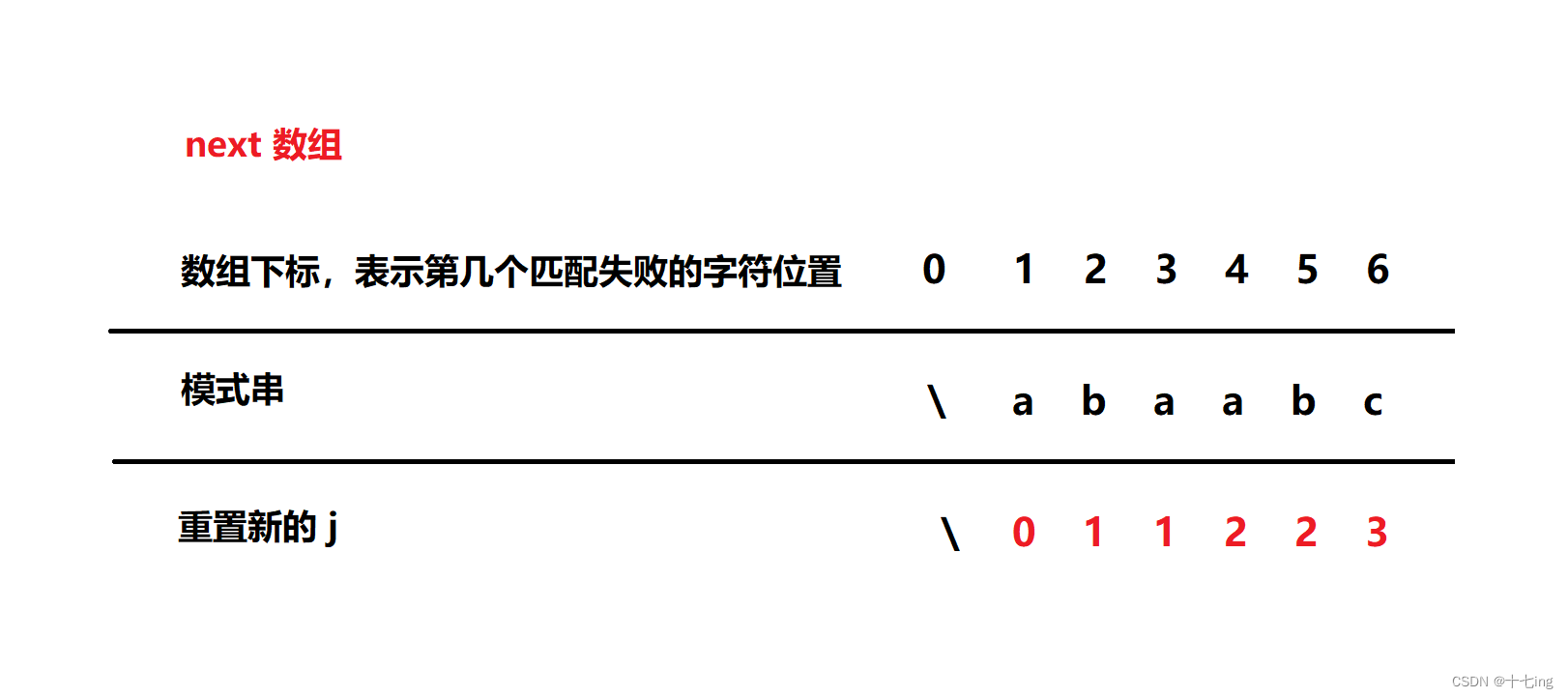
接下来,根据 next 数组来间断地遍历主串序列。
KMP 算法的时间复杂度
最优的时间复杂度:O(1)
最坏的时间复杂度:O(n + m)
讨论最坏的情况:主串长度序列为 n,模式串长度序列为 m.
根据模式串长度序列为 m ,推出 next 数组长度也为 m. 所以在最坏的情况下,一定会遍历 next 数组,时间复杂度为 O(m). 此外,遍历主串的过程中,当字符匹配失败时不产生回溯,即 O(n).
综上所述,KMP 算法的最坏复杂度为 O(n + m)
暴力匹配算法 vs KMP 算法
我们来看一个极端的情况:
// 主串
a a a a a a a a a b
// 模式串
a a a a b
约定用 i 遍历主串,用 j 遍历模式串。
如果用暴力算法,每次匹配到模式串最后一个元素时,i 都要回溯;但使用 KMP 算法时,i 便不会产生回溯,它只会不断地主串右端走。也就是说,暴力算法在每一次失配时,都会重新遍历;而 KMP 算法抓住了模式串的特点,从而省去了回溯的过程,即主串指针 i 只会越来越大。
综上所述,如果我们使用 KMP 算法时,我们需要清楚一件事情,即每次遍历主串的算法关键在于模式串的序列是什么样的,不同的模式串,所对应的 next 数组不同,则每次匹配的方式也不同。
next 数组的训练
模式串 " google "
数组下标: 0 1 2 3 4 5 6
模式串序列: \ g o o g l e
新的 j: \ 0 1 1 1 2 1
模式串 " aaab "
数组下标: 0 1 2 3 4 5
模式串序列: \ a a a a b
新的 j: \ 0 1 2 3 4
KMP 算法的优化
我们先来看一个普通的 KMP 算法的使用例子。
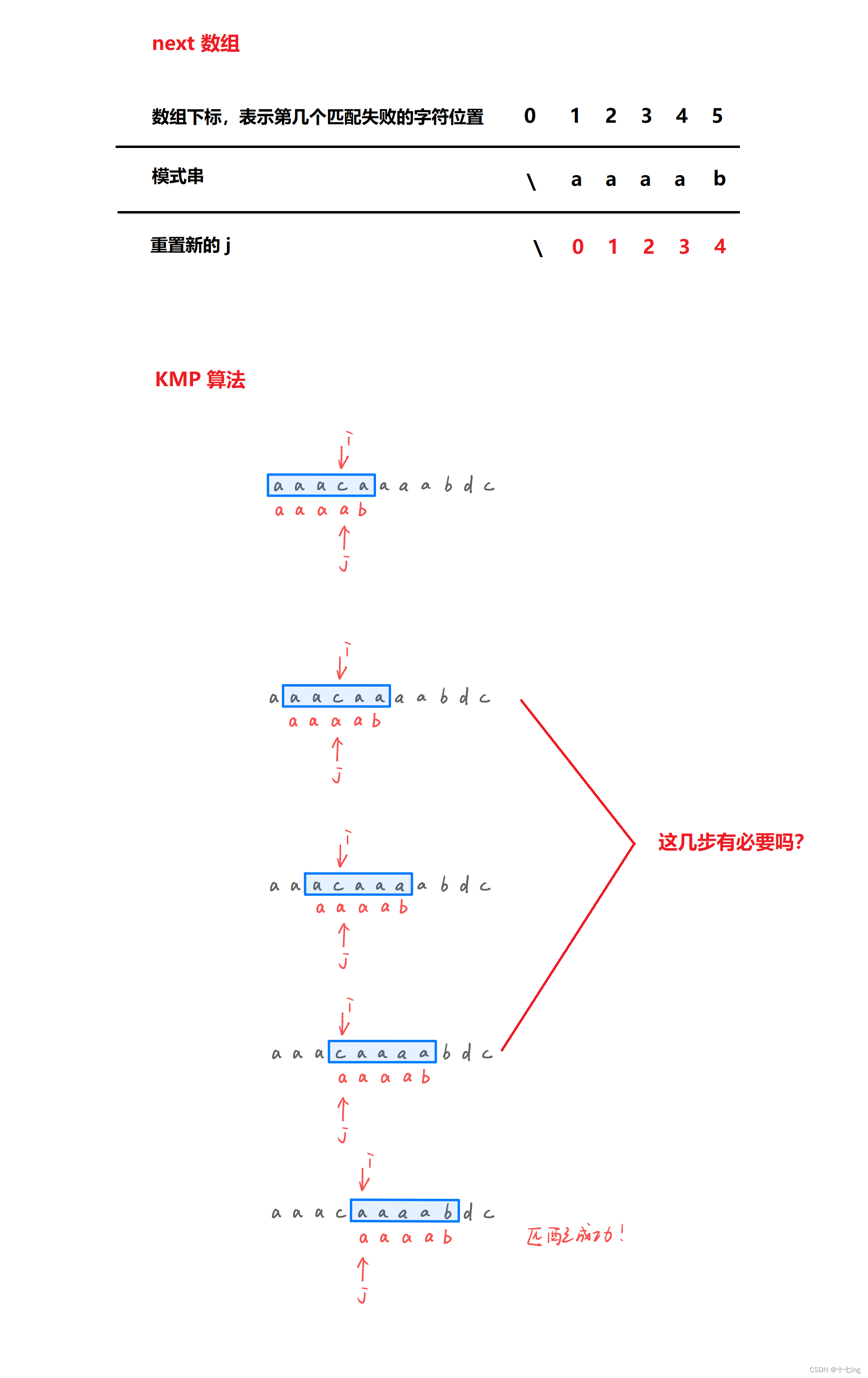
观察上面的主串与模式串的匹配,可以发现,中间三步较为多余。因为第一次匹配的时候,主串中 i=4 的位置与模式串中 j=4 的位置失配,接着就重置 j=3,然而在模式串中 j=3 的位置也是 “字符a”,所以,i=4 与 j=3 在判定时也必然失配。 同样的道理,模式串 j=1、j=2 也是 “字符a”,所以上面的中间三步必然会匹配失败。
综上所述,我们对于 next 数组的元素进行改变,将其变成一个 nextval 数组,而同时不改变 KMP 算法的代码,如下:
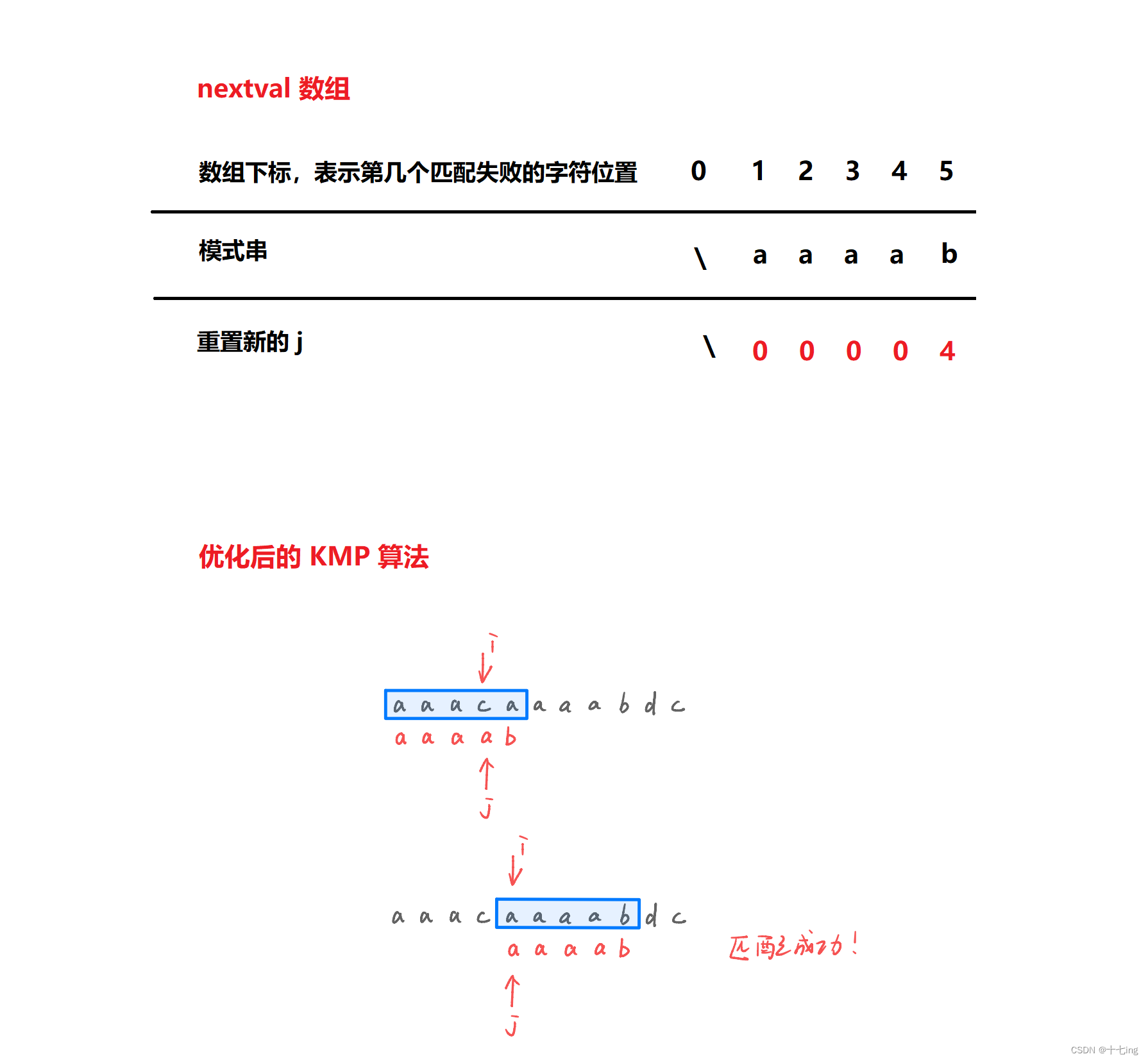
可以发现,在 KMP 算法中,使用了 nextval 数组,将会使得匹配次数减少。
next 数组 转换成 nextval 数组的思想
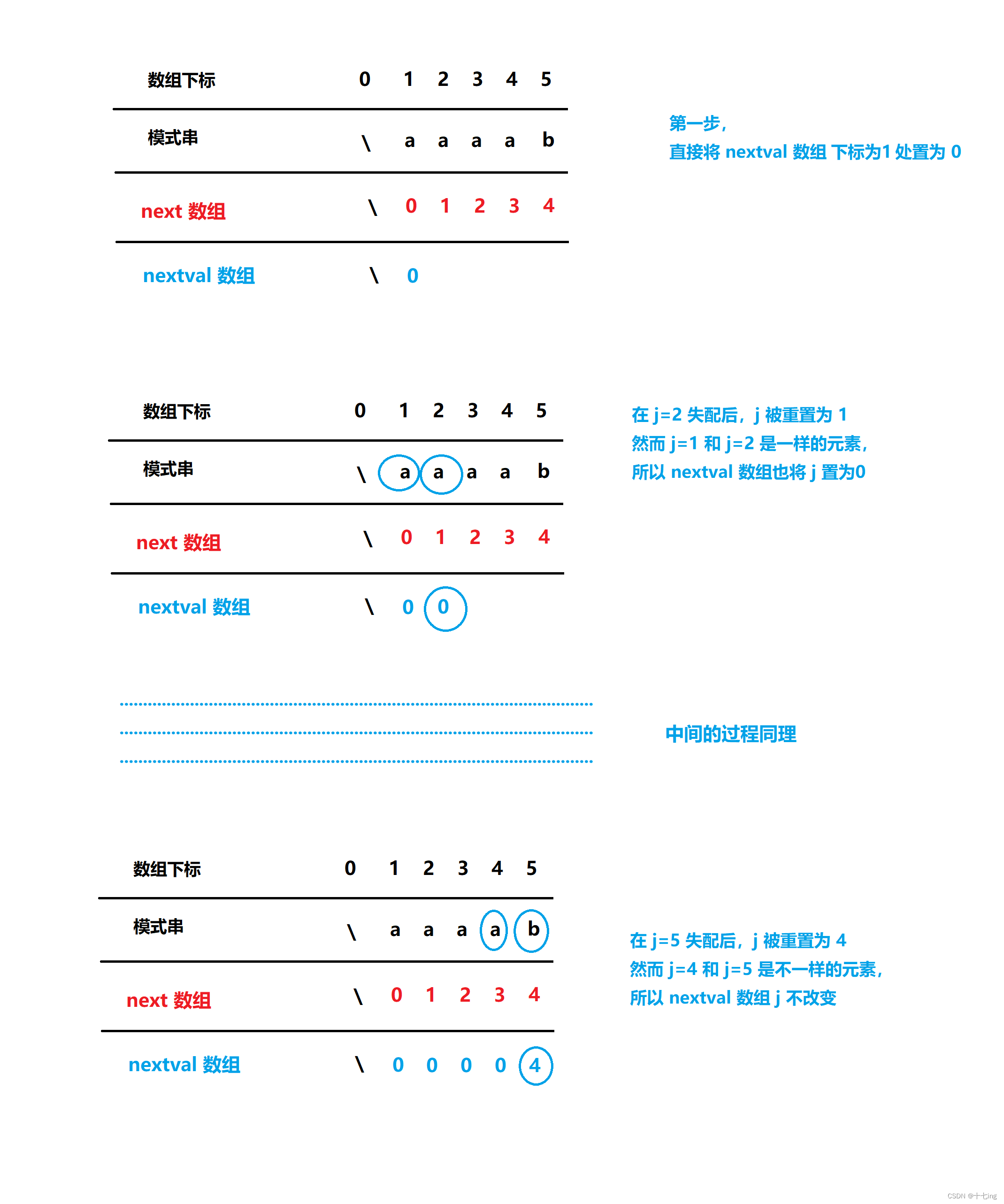

![[C语言]浮点型在内存中的存储](https://img-blog.csdnimg.cn/8dfee3463bd14beda167ba1a48342c7b.png)

![[Linux_]make/Makefile](https://img-blog.csdnimg.cn/26782a673c9946289f713d4861191e26.png)