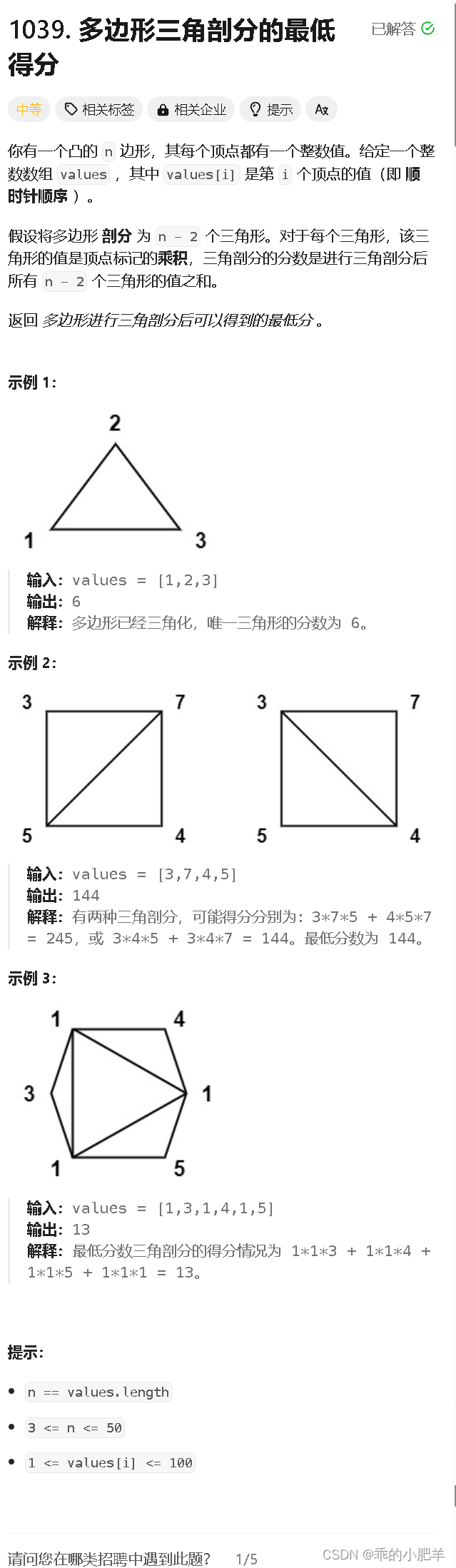
这题的难点在哪部分呢，其实是怎么思考。这道题如果之前没做过类似的话，还是很难看出一些性质的，这题原本的话是没有图片把用例显示的这么详细的。这题中有个很隐晦的点没有说出来

剖出来的三角形是否有交叉，这题中如果加一个三角形之间没有任何交集除了边，会更好理解一点。然后我们就是这么去知道该怎么剖三角形，知道该怎么剖三角形之后。我们再来考虑这是道什么题目，爆搜三角形的乘积的话，我们是n^3，爆搜四边形的乘积的话是这个就不好说了，因为四边形也是由多个是三角形组成的，五边形六边形等等同理

本题中，我们要求的是多边形中能切出的三角形的乘积，我们现在爆搜只是知道多边形中每个三边型的乘积最小值（因为是三角形所以最小值是确定的），并不知道多边形的乘积最小是多少，那么我们三角形其实也算是多边形，但是在本题中他是特殊的三角多边形，而我现在的情况是要求出四边形，五边形，六边型......的乘积最小值，那么知道了这个情况之后，我们再去思考下一步，就是确认是否有递推性质，四边形的最小值是由多个组合的三边形的和中的最小值决定的，那五边形呢？那五边形是不是可以划分为一个四边形和一个三边形，六边形是不是可以划分为一个一个五边形和四边形，我们发现了一个性质，我们可以从三边形的最小值递推到n边形，那么我们就知道了这题目具有递推性质，具有递推性质我们可以用记忆化搜索和动态规划来解决。

前面这些我们是知道整体思路是什么，是本题具有递推性质。那么现在我们就可以根据递推性质来找解决办法了。

那么知道了解决办法后，还有一个难点就是，怎么算这些多边形的乘积。

那么我们现在只知道每一个三角形的乘积，这个三角形的乘积我们是已知的，然后多枚举几个发现一个性质，每个三角形都能把多边形分成三部分，发现三角形可以将整体分成三部分，再继续发现一个性质，不管你以那个三角形分成左右两边，有几个三角形的一条边一定是固定的，也就是外边，那么只要我们枚举外边的任意一个边的所有三角形就可以知道所有组成多边形的三角形最小值了。

知道了怎么算多边形，那么我们现在就是可以确定用什么方法了。动态规划和记忆化搜索都行

先来个记忆化搜索

i < k < j

class Solution {
public:
    int f[110][110];
    int minScoreTriangulation(vector<int>& values) 
    {
        memset(f,0x3f3f3f3f,sizeof(f));

        function<int(int, int)> dfs = [&](int i,int j)->int
        {
             if(abs(i - j) <= 1)
             {
                 return 0;
             }
             if(f[i][j] != 0x3f3f3f3f) return f[i][j];
             for(int k = i + 1;k < j;k++)
             {
                f[i][j] = min(f[i][j],dfs(i,k) + dfs(k,j) + values[i]*values[j]*values[k]);
             }
             return f[i][j];
        };

        dfs(0,values.size() - 1);
        return f[0][values.size() - 1];
    }
};

动态规划：

动态规划部分的话，我们其实在计算的时候，我们的四边形依赖于三边形，五边形依赖于四边形和三边形，六边形同理等等，那么我们就可以根据长度为阶段，然后后面的部分就是固定左和右端点，然后枚举k就行,i < k < j

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 70;

int n;
int a[N];
__int128 f[N][N];
ostream &operator << (ostream &out,__int128 x) {
    if (!x) {
        out << 0;
        return out;
    }
    int stk[110],top = 0;
    while (x) stk[++top] = x % 10,x /= 10;
    for (int i = top;i >= 1;i--) out << stk[i];
    return out;
}
int main()
{
    cin>>n;
    
    for(int i = 1;i <= n;i++)
    {
        cin>>a[i];
    }
    //memset(f,0x3f,sizeof f);
    for(int len = 1;len <= n;len++)
    {
        for(int l = 1,r;r = l + len - 1,r <= n;l++)
        {
            if(len < 3) f[l][r] = 0;
            else
            {
                f[l][r] = 1e29;
            for(int k = l + 1;k < r;k++)
            {
                f[l][r] = min(f[l][r],f[l][k] + f[k][r] + (__int128)a[l] * a[k] * a[r]);
            }
            }
        }
    }
    
    cout<<f[1][n]<<endl;
    return 0;
}