1 初始强化学习
强化学习是机器通过与环境交互来实现目标的一种计算方法。
机器和环境的一轮交互是指,机器在环境的一个状态下做一个动作决策,把这个动作作用到环境当中,这个环境发生相应的改变并且将相应的奖励反馈和下一轮状态传回机器
这种交互是迭代进行的,机器的目标是最大化在多轮交互过程中获得的累积奖励的期望
智能体和环境之间具体的交互方式如下图所示。在每一轮交互中,智能体感知到环境目前所处的状态,经过自身的计算给出本轮的动作,将其作用到环境中;环境得到智能体的动作后,产生相应的即时奖励信号并发生相应的状态转移。智能体则在下一轮交互中感知到新的环境状态,依次类推。
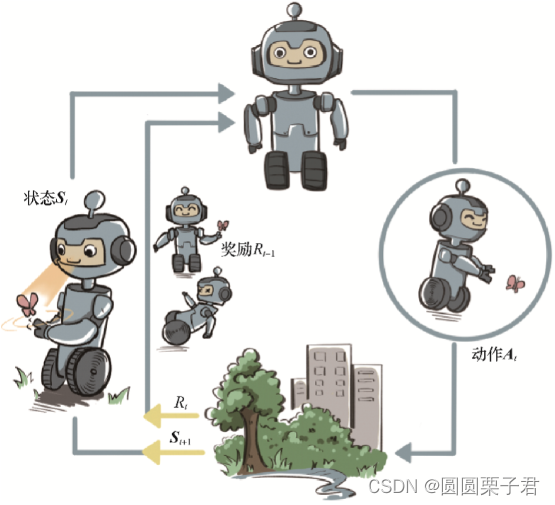
智能体有3种关键要素,即感知、决策和奖励
感知。智能体在某种程度上感知环境的状态,从而知道自己所处的现状
决策。智能体根据当前的状态计算出达到目标需要采取的动作的过程叫作决策
奖励。环境根据状态和智能体采取的动作,产生一个标量信号作为奖励反馈
智能体和环境每次进行交互时,环境会产生相应的奖励信号,其往往由实数标量来表示。这个奖励信号一般是诠释当前状态或动作的好坏的及时反馈信号,好比在玩游戏的过程中某一个操作获得的分数值。整个交互过程的每一轮获得的奖励信号可以进行累加,形成智能体的整体回报(return),好比一盘游戏最后的分数值。
在强化学习中,我们关注回报的期望,并将其定义为价值(value),这就是强化学习中智能体学习的优化目标。
2 多臂老虎机
多臂老虎机不存在状态信息,只有动作和奖励,算是最简单的“和环境交互中的学习”的一种形式。多臂老虎机中的探索与利用(exploration vs. exploitation)问题一直以来都是一个特别经典的问题
2.1 问题介绍
有一个拥有K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励的概率分布R。我们每次拉动其中一根拉杆,就可以从该拉杆对应的奖励概率分布中获得一个奖励r。我们在各根拉杆的奖励概率分布未知的情况下,从头开始尝试,目标是在操作T次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的,因此我们需要在“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”中进行权衡。“采用怎样的操作策略才能使获得的累积奖励最高”便是多臂老虎机问题。
2.2 形式化描述

2.3 累计懊悔
下述的Q(a)期望奖励,应该是,概率分布中,对应的r乘以对应的概率,然后求和。称之为期望

2.4 估计期望奖励
为了知道拉动哪一根拉杆能获得更高的奖励,我们需要估计拉动这根拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性,所以需要多次拉动一根拉杆,然后计算得到的多次奖励的期望,其算法流程如下所示。


2.5 探索与利用的平衡
在上述框架中,还没有一个策略告诉我们应该采取哪个动作,即拉动哪根拉杆,所以接下来我们将学习如何设计一个策略。例如,一个最简单的策略就是一直采取第一个动作,但这就非常依赖运气的好坏。如果运气绝佳,可能拉动的刚好是能获得最大期望奖励的拉杆,即最优拉杆;但如果运气很糟糕,获得的就有可能是最小的期望奖励。在多臂老虎机问题中,一个经典的问题就是探索与利用的平衡问题。
探索(exploration)是指尝试拉动更多可能的拉杆,这根拉杆不一定会获得最大的奖励,但这种方案能够摸清楚所有拉杆的获奖情况。例如,对于一个 10 臂老虎机,我们要把所有的拉杆都拉动一下才知道哪根拉杆可能获得最大的奖励。
利用(exploitation)是指拉动已知期望奖励最大的那根拉杆,由于已知的信息仅仅来自有限次的交互观测,所以当前的最优拉杆不一定是全局最优的。例如,对于一个 10 臂老虎机,我们只拉动过其中 3 根拉杆,接下来就一直拉动这 3 根拉杆中期望奖励最大的那根拉杆,但很有可能期望奖励最大的拉杆在剩下的 7 根当中,即使我们对 10 根拉杆各自都尝试了 20 次,发现 5 号拉杆的经验期望奖励是最高的,但仍然存在着微小的概率—另一根 6 号拉杆的真实期望奖励是比 5 号拉杆更高的。

2.6 ϵ-贪心算法


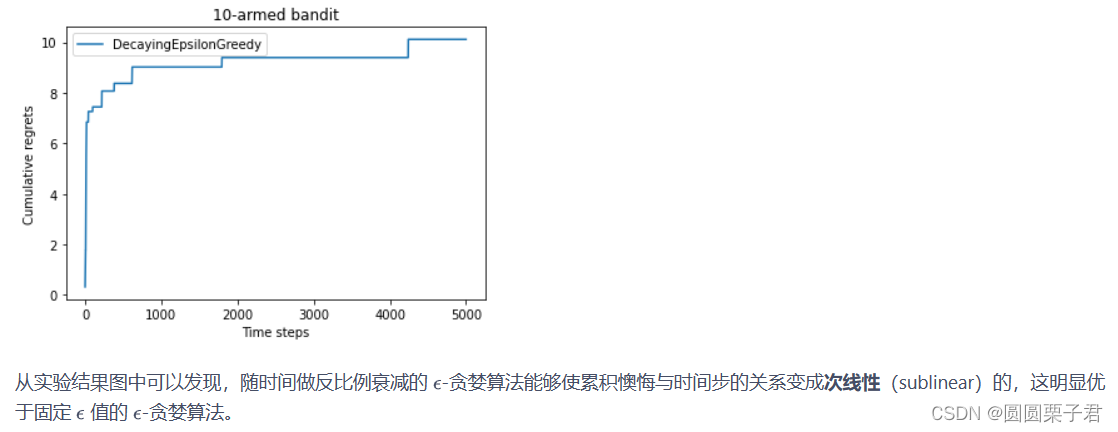
上置信界算法和汤普森采样算法暂不介绍,有兴趣自己看,我用到的时候再看
2.7 总结
探索与利用是与环境做交互学习的重要问题,是强化学习试错法中的必备技术
多臂老虎机问题是研究探索与利用技术理论的最佳环境。了解多臂老虎机的探索与利用问题,对接下来我们学习强化学习环境探索有很重要的帮助。
多臂老虎机问题与强化学习的一大区别在于其与环境的交互并不会改变环境,即多臂老虎机的每次交互的结果和以往的动作无关,所以可看作无状态的强化学习