本篇博客和接下来的几篇博客主要讲解一下动态规划中的股票问题系列，本篇博客主要讲解121. 买卖股票的最佳时机和122.买卖股票的最佳时机II。

121. 买卖股票的最佳时机

题目：

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：

[7,1,5,3,6,4]

输出：

5

解释：

在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：

prices = [7,6,4,3,1]

输出：

0

解释：

在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 105
• 0 <= prices[i] <= 104

思路：

本题也可以用贪心来做，因为股票就买卖一次，那么贪心的想法很自然就是取最左最小值，取最右最大值，那么得到的差值就是最大利润。

不过贪心只适合解决部分股票系列问题，而动态规划才是解决股票问题的模板。

动规五部曲分析如下：

1. 确定dp数组（dp table）以及下标的含义

dp[i][0] 表示第i天持有股票所得最多现金 ，本题中只能买卖一次，持有股票之后哪还有现金呢？

其实一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]， 这是一个负数。

dp[i][1] 表示第i天不持有股票所得最多现金

注意这里说的是“持有”，“持有”不代表就是当天“买入”！也有可能是昨天就买入了，今天保持持有的状态。

2. 确定递推公式

如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来

• 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
• 第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]

那么dp[i][0]应该选所得现金最大的，所以dp[i][0] = max(dp[i - 1][0], -prices[i]);

如果第i天不持有股票即dp[i][1]， 也可以由两个状态推出来

• 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
• 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]

同样dp[i][1]取最大的，dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i -
1][0]);

3. dp数组如何初始化

由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出

其基础都是要从dp[0][0]和dp[0][1]推导出来。

那么dp[0][0]表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以dp[0][0] = -prices[0];

dp[0][1]表示第0天不持有股票，不持有股票那么现金就是0，所以dp[0][1] = 0;

4. 确定遍历顺序

从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的，那么一定是从前向后遍历。

5. 举例推导dp数组

以示例1，输入：[7,1,5,3,6,4]为例，dp数组状态如下：

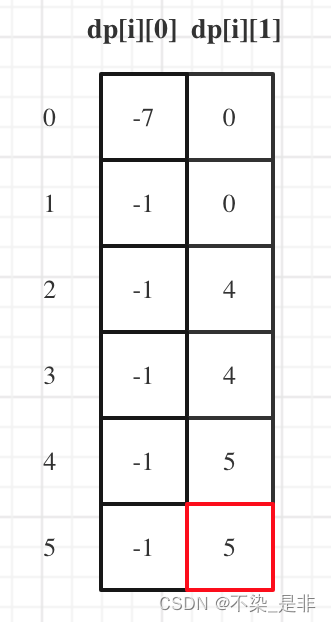
dp[5][1]就是最终结果。

为什么不是dp[5][0]呢？

因为本题中不持有股票状态所得金钱一定比持有股票状态得到的多！

代码及详细注释：

贪心：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        low = float("inf")
        result = 0
        for i in range(len(prices)):
            low = min(low, prices[i]) #取最左最小价格
            result = max(result, prices[i] - low) #直接取最大区间利润
        return result

• 时间复杂度：O(n)
• 空间复杂度：O(1)

动态规划：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        dp = [[0] * 2 for _ in range(len(prices))]  # 创建二维列表dp，用于存储每天结束时的最大利润，0表示持有股票，1表示不持有股票
        dp[0][0] = -prices[0]  # 第一天持有股票的最大利润为负的股票价格
        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i - 1][0], -prices[i])  # 第i天持有股票的最大利润为前一天持有股票的最大利润和当天买入股票的最大利润中的较大值
            dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i- 1][0])  # 第i天不持有股票的最大利润为前一天不持有股票的最大利润和当天卖出股票的最大利润中的较大值
        return dp[len(prices) - 1][1]  # 返回最后一天不持有股票的最大利润

• 时间复杂度：O(n)
• 空间复杂度：O(n)

动态规划优化：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        dp0, dp1 = -prices[0], 0 #注意这里只维护两个常量，因为dp0的更新不受dp1的影响
        for i in range(1, length):
            dp1 = max(dp1, dp0 + prices[i])
            dp0 = max(dp0, -prices[i])
        return dp1

• 时间复杂度：O(n)
• 空间复杂度：O(1)

122.买卖股票的最佳时机II

题目：

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：

prices = [7,1,5,3,6,4]

输出：

7

解释：

在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。

示例 2：

输入：

prices = [1,2,3,4,5]

输出：

4

解释：

在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。

示例 3：

输入：

prices = [7,6,4,3,1]

输出：

0

解释：

在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示：

• 1 <= prices.length <= 3 * 104
• 0 <= prices[i] <= 104

思路：

本题和121. 买卖股票的最佳时机 的唯一区别是本题股票可以买卖多次了（注意只有一只股票，所以再次购买前要出售掉之前的股票）

在动规五部曲中，这个区别主要是体现在递推公式上，其他都和121. 买卖股票的最佳时机 一样一样的。

所以我们重点讲一讲递推公式。

这里重申一下dp数组的含义：

• dp[i][0] 表示第i天持有股票所得现金。
• dp[i][1] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来

• 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
• 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]

注意这里和121. 买卖股票的最佳时机 唯一不同的地方，就是推导dp[i][0]的时候，第i天买入股票的情况。

在121. 买卖股票的最佳时机中，因为股票全程只能买卖一次，所以如果买入股票，那么第i天持有股票即dp[i][0]一定就是 -prices[i]。

而本题，因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润。

那么第i天持有股票即dp[i][0]，如果是第i天买入股票，所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即：dp[i - 1][1] - prices[i]。

再来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来

• 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
• 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]

注意这里和121. 买卖股票的最佳时机就是一样的逻辑，卖出股票收获利润（可能是负值）

代码如下：

        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]) # 仅此处跟上题不同
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])

代码及详细注释：

贪心法：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        result = 0
        for i in range(1, len(prices)):
            result += max(prices[i] - prices[i - 1], 0)
        return result

• 时间复杂度：O(n)
• 空间复杂度：O(1)

动态规划：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        dp = [[0] * 2 for i in range(len(prices))]  # 创建二维列表dp，用于存储每天结束时的最大利润，0表示持有股票，1表示不持有股票
        dp[0][0] = -prices[0]  # 第一天持有股票的最大利润为负的股票价格
        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])  # 第i天持有股票的最大利润为前一天持有股票的最大利润和当天买入股票的最大利润中的较大值
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])  # 第i天不持有股票的最大利润为前一天不持有股票的最大利润和当天卖出股票的最大利润中的较大值
        return dp[-1][1]  # 返回最后一天不持有股票的最大利润

• 时间复杂度：O(n)
• 空间复杂度：O(n)

动态规划优化：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        dp0 = -prices[0]
        dp1 = 0
        for i in range(1, len(prices)):
            dp0 = max(dp0, dp1 - prices[i])
            dp1 = max(dp1, dp0 + prices[i])
        return dp1

• 时间复杂度：O(n)
• 空间复杂度：O(1)