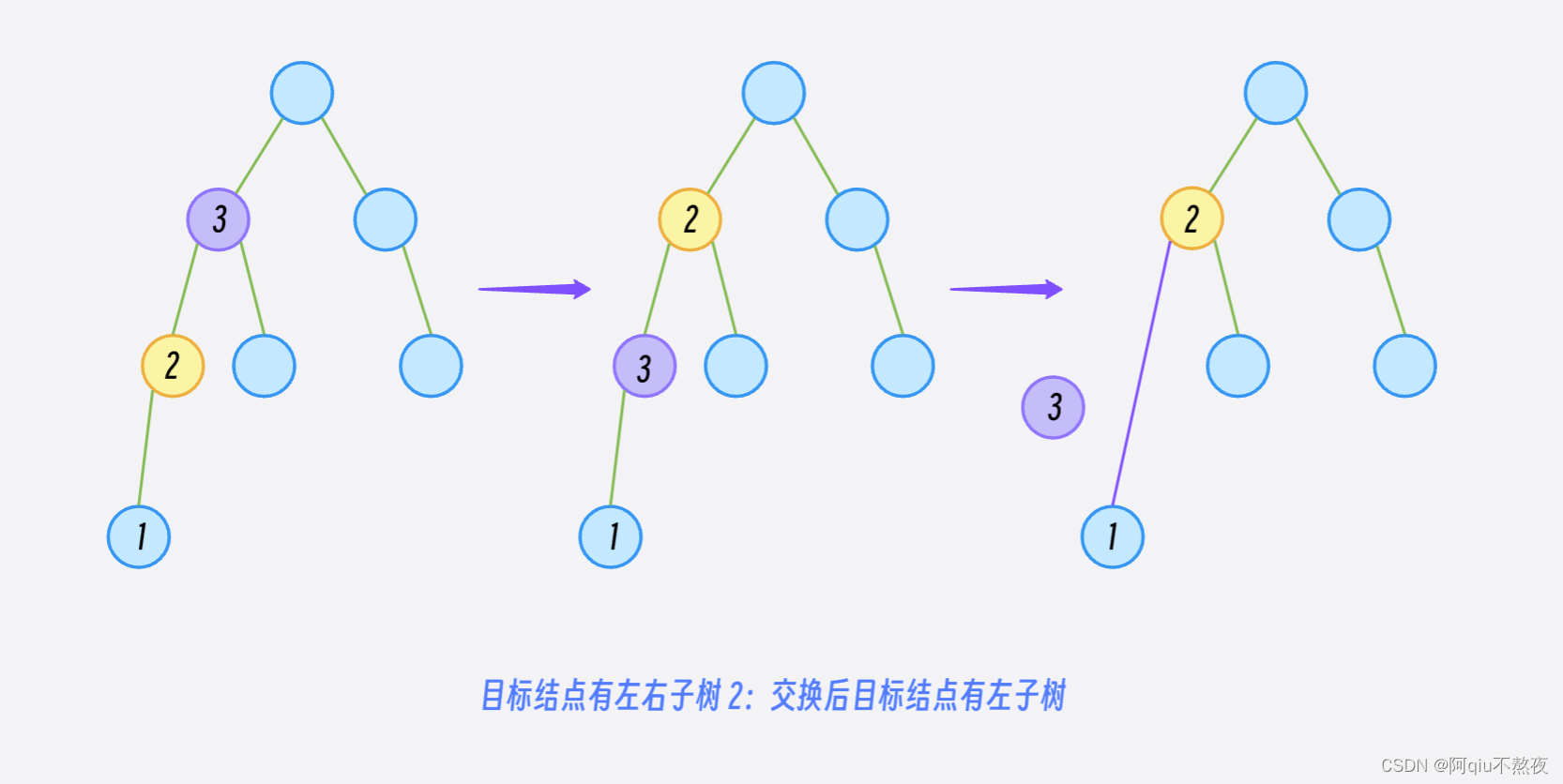
非递减子序列

这道题与子集II比较相似，子序列也是子集，而且这里数组中也包含重复元素。但是这道题要有序的序列，所以不能对原来的数组先进行排序。但我们前一篇文章总结过：子集问题中涉及重复元素时，是需要排序的。
这里还需要细化总结一下，树层去重可以做到去除元素和排列顺序都相同的组合，无法去除 [4,1,4] 和 [4,4,1] 这样顺序不同的情况。而经过排序之后这个问题就解决了，这道题本身就限制了元素顺序，所以只要能去除元素和顺序都相同的重复组合就行了。

class Solution{
public:
	vector<vector<int>> result;
	vector<int> path;
	void backtracking(vector<int>& nums, int startIndex){
		if(path.size() > 1){  // 要求path中有两个及以上元素
			result.push_back(path);  // 不要return，因为要在递归过程中始终记录
		}
		unordered_set<int> uset;  // 进行树层去重
		for(int i = startIndex; i < nums.size(); i++){
			if((!path.empty() && nums[i] < path.back()) 
			|| uset.find(nums[i]) != uset.end()){
				// 如果不空，当前元素破坏了单调不减，或者树层发生了重复，放弃当前元素
				continue;
			}
			uset.insert(nums[i]);
			path.push_back(nums[i]);
			backtracking(nums, i + 1);  // 元素只能使用一次
			path.pop_back();
		}
	}
	vector<vector<int>> findSubsequences(vector<int>& nums){
		result.clear();
		path.clear();
		backtracking(nums, 0);
		return result;
	}
};

这里也可以用数组实现哈希表，代码的性能更好，因为数组中元素值范围不大。

全排列

全排列问题需要注意 [1,2] 和 [2,1] 是两种不同的排列，因此不需要 startIndex 避免组合的重复出现。但是仍然需要在树枝上记录用过的元素，避免一个排列中元素重复。

class Solution{
public:
	vector<vector<int>> result;
	vector<int> path;
	void backtracking(vector<int>& nums, vector<bool>& used){
		if(path.size() == nums.size()){
			result.push_back(path);
			return;
		}
		for(int i = 0; i < nums.size(); i++){
			if(used[i] == true)  continue;
			used[i] = true;
			path.push_back(nums[i]);
			backtracking(nums, used);
			path.pop_back();
			used[i] = false;
		}
	}
	vector<vector<int>> permute(vector<int>& nums){
		result.clear();
		path.clear();
		vector<bool> used(nums.size(), false);
		backtracking(nums, used);
		return result;
	}
};

全排列II

这道题与组合问题II也是相似的，数组中有重复的元素。所以仍然可以借鉴全排列和组合问题II的思路。注意需要判断used[i - 1]，因为不能用 startIndex 在树枝上做去重。有趣的是，判断used[i - 1] == true或used[i - 1] == false都是可以的，可以画图验证做树层去重剪枝效果更好。

class Solution{
public:
	vector<vector<int>> result;
	vector<int> path;
	void backtracking(vector<int>& nums, vector<bool>& used){
		if(path.size() == nums.size()){
			result.push_back(path);
			return;
		}
		for(int i = 0; i < nums.size(); i++){
			if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
				continue;
			}
			if(!used[i]){
				used[i] = true;
				path.push_back(nums[i]);
				backtracking(nums, used);
				path.pop_back();
				used[i] = false;
			}
		}
	}
	vector<vector<int>> permuteUnique(vector<int>& nums){
		result.clear();
		path.clear();
		sort(nums.begin(), nums.end());
		vector<bool> used(nums.size(), false);
		backtracking(nums, used);
		return result;
	}
};