P1044 [NOIP2003 普及组] 栈

方法一：递推dp

思路：

求n的总数，我们可以分解成n在第i（1<=i<=n)位置输出讨论。

我们用a[i][j]表示数i在第j位置输出的情况总数，ans[i][j]表示数i在第1--j位置输出总数和

1，我们发现，a[i][1]=1，理由下面说明

2，我们观察到，在讨论n所在位置的情况时，我们发现，如果位置在n后面的数，一定是按递减输出（容易证明，位置在n后面，说明他们在n输出前都在栈里面，而栈是越小越底层越晚输出），所以，我们变成只需要考虑n在第i个位置前面的1--i-1位置的输出情况

3，考虑n在第i个位置前面的1--i-1位置的输出情况即a[n][i]==ans[n-1][i]

证明如下：

我们在位置i输出n，首先需要把前面n-1个数处理好（要么输出，要么放入栈里面）。如何处理如下图

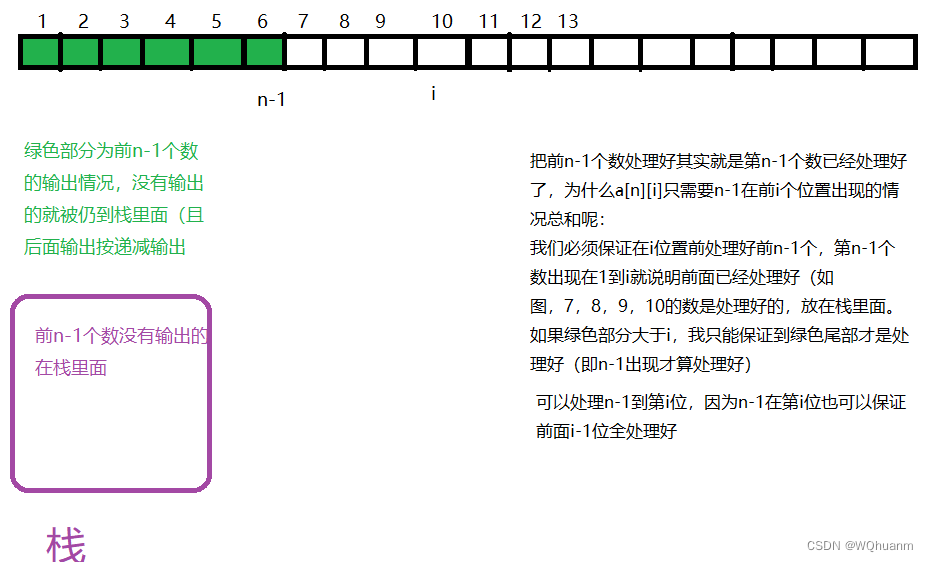
 4,还注意到，第n个放最后一位，情况数其实就是前面n-1个情况总数

第n个放倒数第二位也是等于前面n-1个情况总数，因为前面n-1个放倒数第二位，与放栈里面等第n个放完再输出是一样的，即a[n][n-1]==ans[n-1][n-1]!=ans[n-1][n-2]

解决完，就可以递推得到答案

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
const int INF = 0x3f3f3f3f;
const int N = 20;

int a[N][N], ans[N][N];
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i)//求i个数的情况
		{
			a[i][i] = a[i][i - 1] = ans[i - 1][i - 1];//第i个放最后一位，或者倒数第二位的情况等于前面i-1所有可能情况
			a[i][1] = 1;//第i个数放第一个，后面都是固定的，情况1种，这个放a[i][i] = a[i][i - 1] = ans[i - 1][i - 1];后面是因为前面得到的可能更改a[i][1]
			for (int j = 2; j <= i - 2; ++j)a[i][j] = ans[i - 1][j];//j从i放第二位到倒数第三位处理
			for (int j = 1; j <= i; ++j)ans[i][j] = ans[i][j - 1] + a[i][j];//处理求和
		}
	cout << ans[n][n];
	return 0;
}

方法二，卡特兰数

思路：

进出栈问题实际是经典的卡特兰数问题

我们设函数h[i]表示在i个数的输出情况总数，

我们设k最后一个出栈，发现前面1到k-1的进出栈情况可以看成一个整体，后面k+1到n可以看出一个整体，为什么：

前面k-1个数在k进栈前要先进栈，又因为k最后进栈，那么一旦k进栈，栈里面绝对没有数，k才可以放入最底层，所以前面k-1个数是一个整体，处理k到n个数时，k一直在底层旁观，所以后面是一个整体

那么情况数就是h[k-1]*h[n-k],所以h[n]就是h[j]*h[n-1+j]的求和（0<=j<=n-1，j从0位到倒数第二位)。

显然h[1]=1,我们规定h[0]=1，因为乘法

代码更简洁

#include <bits/stdc++.h>
using namespace std;
#define ll     long long
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
const int INF = 0x3f3f3f3f;
const int N = 20;
int h[N];

int main()
{
	h[0] = h[1] = 1;
	int n;
	cin >> n;
	for (int i = 2; i <= n; ++i)for (int j = 0; j <= i - 1; ++j)h[i] += h[j] * h[i - 1 - j];//求和
	cout << h[n];
	return 0;
}