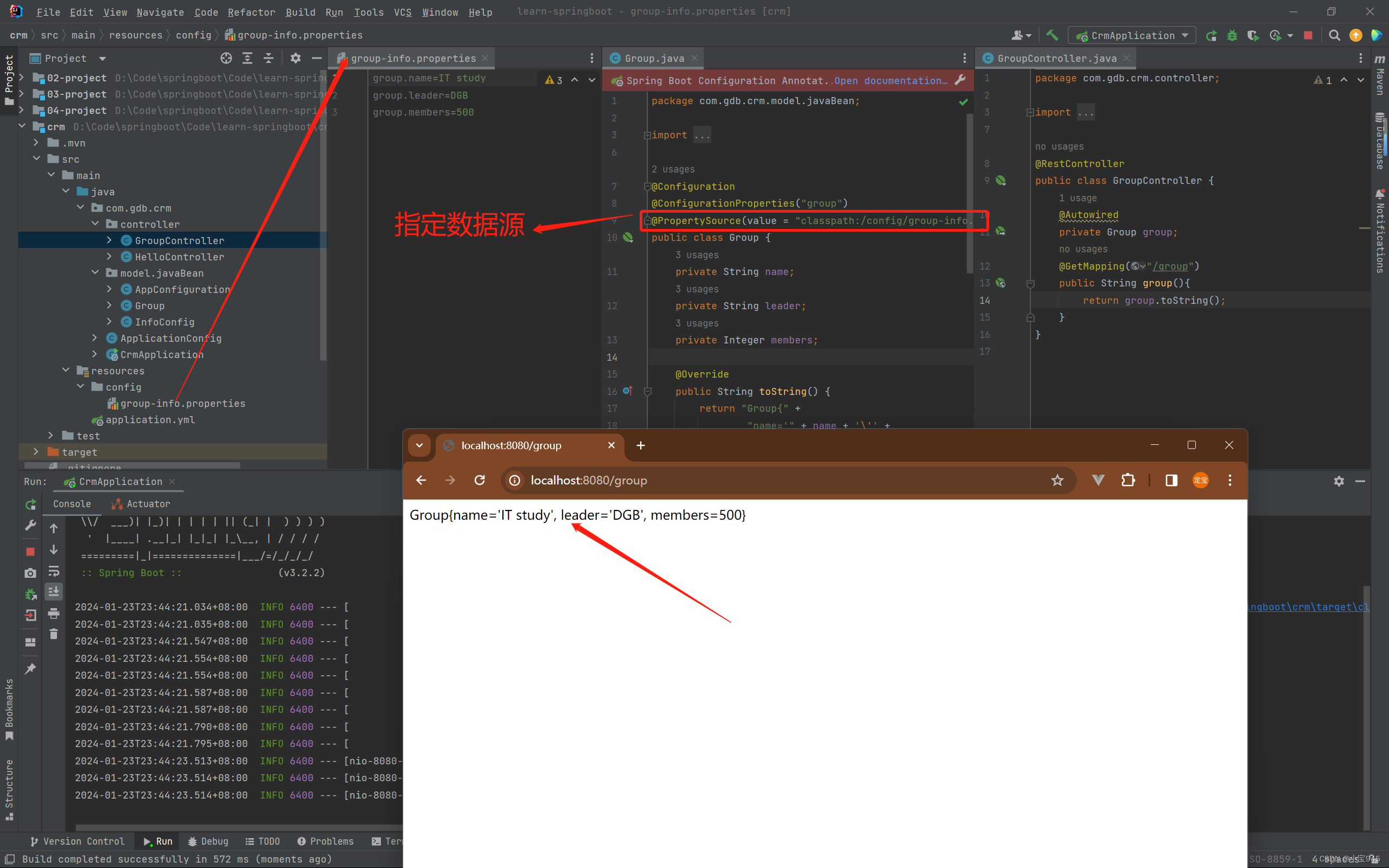
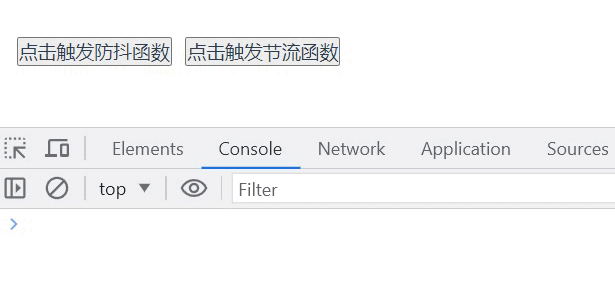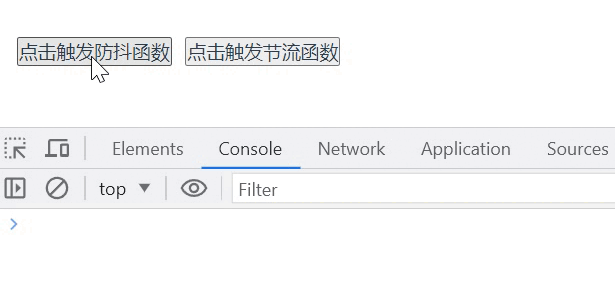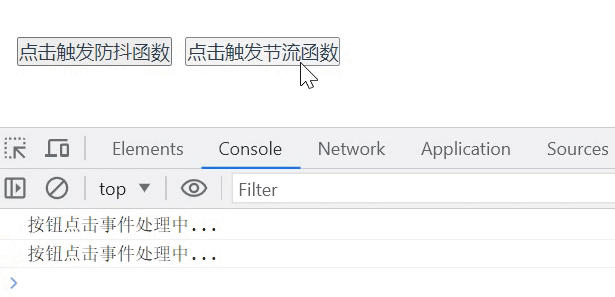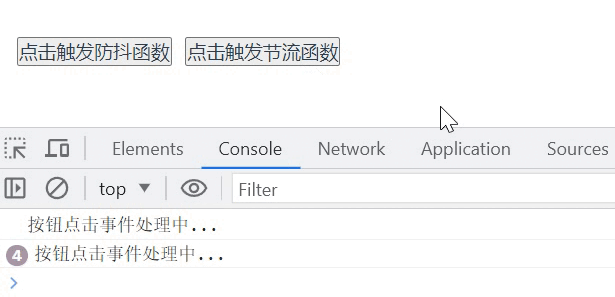
前言：

  上一期分析了快速排序的三种写法，这三种写法有一个相同点，都是采用递归形式来实现的，那么有没有非递归的方法实现呢？答案是当然有，用非递归的方法实现快速排序，其实可以借助数据结构中的栈来模拟实现递归的过程。

思路图分析:

  因为使用c语言写的，所以需要我们自己写一个栈，栈的实现我这里不再过多赘述，我会把栈的码放在最后。假如我们现在有下面这组数组，我们要对它进行排序。（注意下面的数字代表下标）

好，接下来开始用栈模拟递归：（图中栈中的数字均表示下标）

1.第一次入栈：

将整个数组入栈，也就是下标为0-8

2.第一次出栈：

每次出栈，对出栈的下标区间进行一次部分排序，这里的部分排序，就是选出key，将其放在正确的位置有3种实现方法，如有不懂可以看我上一期博客，这里我选的是双指针法。第一次出栈进行第一趟部分排序后，数组的元素变为如下图：

此时的key也就是45就被放在了正确的位置，也就是左边的元素都比它小，右边的元素都比它大。

然后再将key的左区间和右区间分别入栈，也就是0-3和5-8

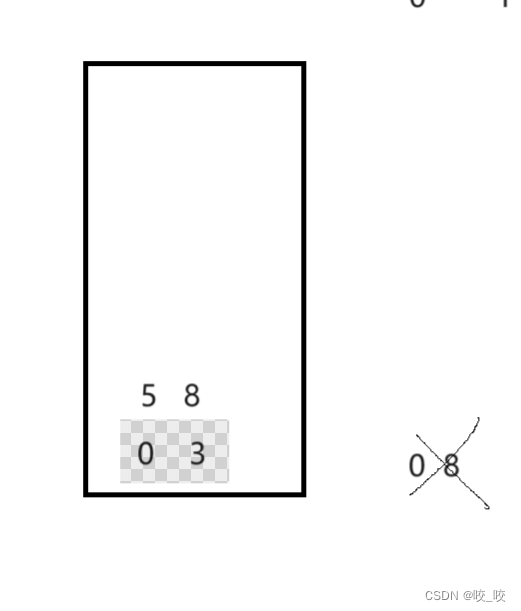
3.第二次出栈：

根据栈的性质后入先出，所以我们让5-8出栈：

跟上面一样，每次出栈对相应区间进行一次部分排序，排序完如下图：

因为在对这个区间进行部分排序时，67被选为key，此时67的右边已经全部比他大，所以排完序后不变，然后再将key的左区间和右区间分别入栈（注意此时的左区间和右区间加起来应该是5-8，因为我们是对5-8这个区间进行部分排序的，而不是0-8），左区间没有元素了也就是4-4，右区间6-8，注意这时候左区间就已经没有必要入栈了（因为少于2个元素必定有序了），只需将没排好序的右区间入栈即可：

4.第二次入栈：

然后只要栈不为空，我们就出栈然后进行和上面一样的操作。

现在就不难感受出，这其实是在模拟递归的过程。

5.第三次出栈：

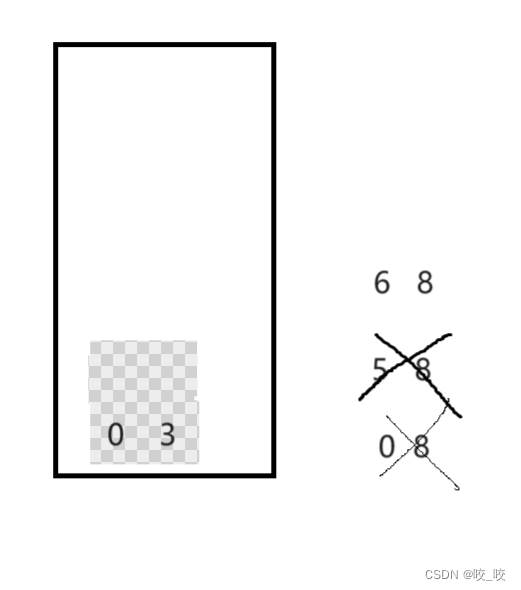
部分排序后如下图：

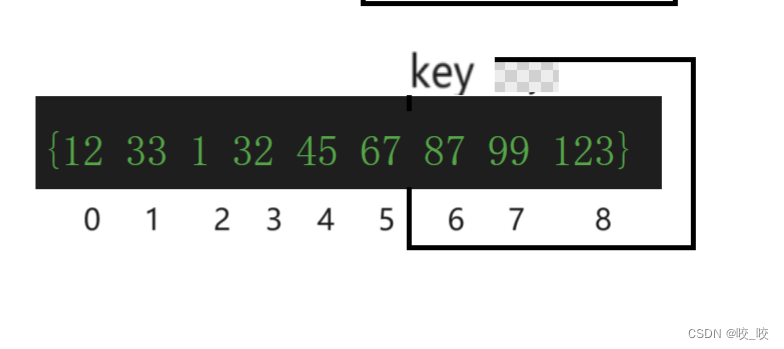
跟上面同理左区间少于两个元素不必入栈，右区间入栈7-8

6.第三次入栈：

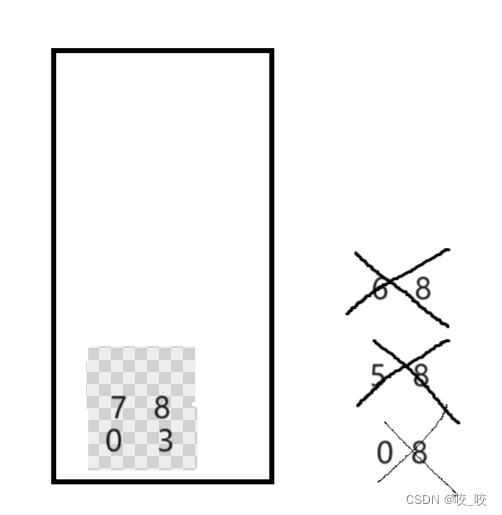
然后又是7-8出栈，再判断是否入栈，出栈，判断是否入栈，出栈，判断是否入栈一直重复，直到栈里面为空，就排好了，所以循环的使用在这里面也很重要，下面来看一下全部代码吧！

代码：

#include<stdio.h>
#include"Stack.h"

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

int PartSort3(int* a, int begin, int end)//双指针法
{
	int keyi = begin;
	int prev = begin;
	int cur = begin + 1;
	while (cur <= end)
	{
		if (a[cur] < a[keyi] && ++prev != a[cur])
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	keyi = prev;
	return keyi;
}

void QuickSortNonR(int* a, int begin, int end)
{
	Stack s;
	StackInit(&s);
	StackPush(&s, end);
	StackPush(&s, begin);//第一次入栈首尾下标
	while (!StackEmpty(&s))//栈只要不为空，就一直出栈，判断是否入栈......
	{
		int left = StackTop(&s);
		StackPop(&s);
		int right = StackTop(&s);
		StackPop(&s);//出栈，首元素下标放在left，尾元素下标放在right，很形象
		int keyi = PartSort3(a, left, right);//进行一次部分排序，并将最后key的下标返回
		//[left,keyi-1]keyi[keyi+1,right]//拆分成的区间
		//下面为判断是否入栈
		if (left < keyi - 1)//如果左区间元素个数不少于2
		{
			StackPush(&s, keyi - 1);
			StackPush(&s, left);//入栈
		}
		if (keyi + 1 < right)//如果右区间元素个数不少于2
		{
			StackPush(&s, right);
			StackPush(&s, keyi+1);//入栈
		}
	}
	//循环结束，栈为空，排序完成
	StackDestroy(&s);//销毁栈
}

栈的实现代码：

#include"Stack.h"
void StackInit(Stack* ps)//初始化栈
{
	ps->a = NULL;
	ps->top = -1;
	ps->capacity = 0;
}
void StackPush(Stack* ps, STDateType data)//入栈
{
	StackCheck(ps);
	ps->top++;
	ps->a[ps->top] = data;
}
void StackCheck(Stack* ps)//检查容量
{
	assert(ps);
	if(ps->top+1==ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDateType* tmp = (STDateType*)realloc(ps->a, sizeof(STDateType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc");
			return;
		}
		else
		{
			ps->a = tmp;
			ps->capacity = newcapacity;
		}
	}
}
bool StackEmpty(Stack* ps)//判空函数
{
	return ps->top == -1;
}
STDateType StackTop(Stack* ps)//获取栈顶元素
{
	assert(ps);
	assert(ps->top+1 > 0);
	return ps->a[ps->top];
}
void StackPop(Stack* ps)//出栈
{
	assert(ps);
	ps->top--;
}
int StackSize(Stack* ps)//获取栈中有效元素的个数
{
	assert(ps);
	return ps->top+1;
}
void StackDestroy(Stack* ps)//销毁栈
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = -1;
	ps->capacity = 0;
}

栈的头文件：

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int STDateType;
typedef struct Stack
{
	STDateType* a;
	int top;//栈顶
	int capacity;//容量
}Stack;
void StackInit(Stack* ps);//初始化栈
void StackCheck(Stack* ps);//检查容量
void StackPush(Stack* ps, STDateType data);//入栈
void StackPop(Stack* ps);//出栈
bool StackEmpty(Stack* ps);//判空函数
STDateType StackTop(Stack* ps);//获取栈顶元素
int StackSize(Stack* ps);//获取栈中有效元素的个数
void StackDestroy(Stack* ps);//销毁栈