详解线性分组码（linear code）

news2024/10/1 17:38:13

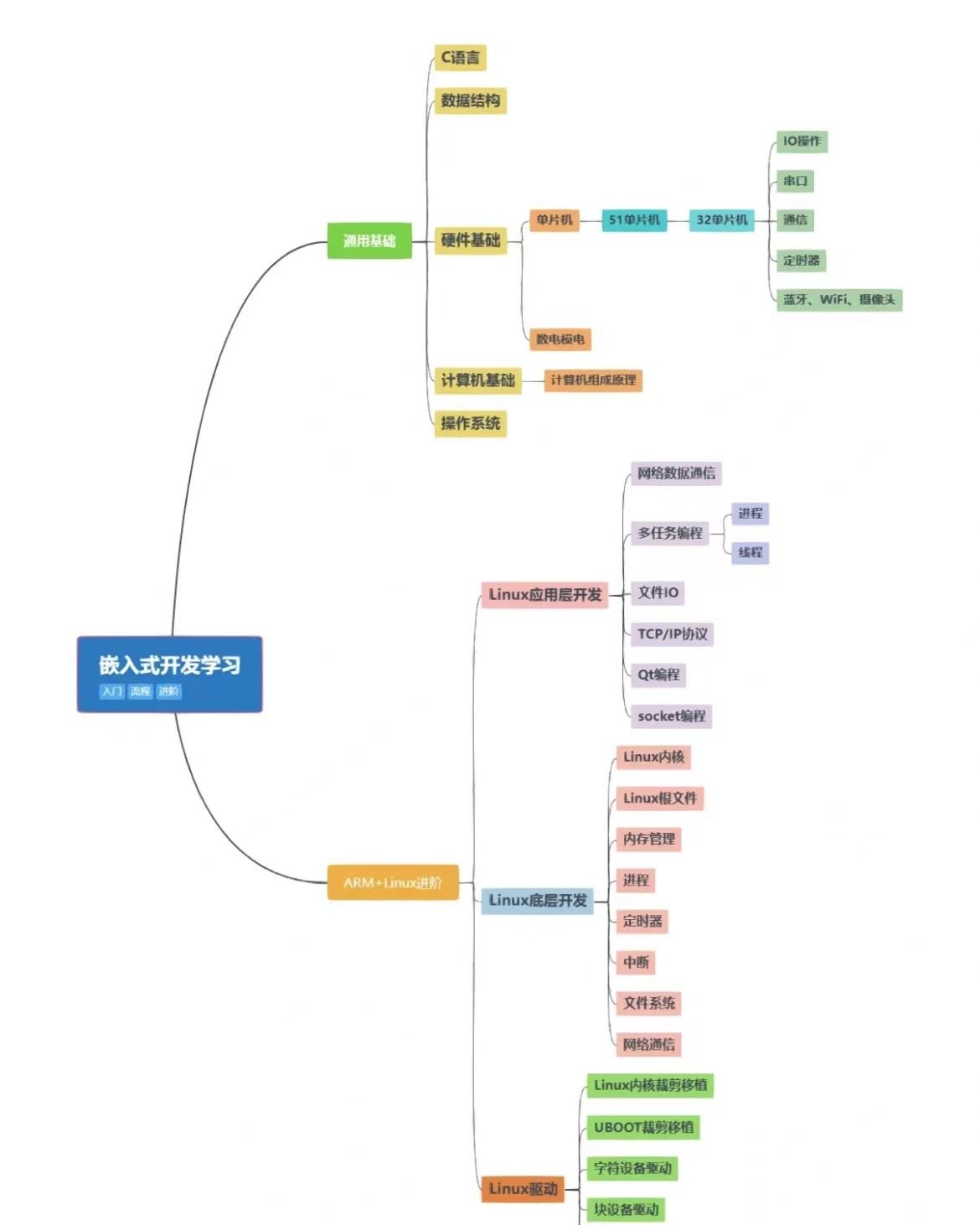
一. 介绍

二. 线性分组码

三. 生成矩阵

四. 对偶编码

五. 校验矩阵

六. 陪集编码

七. 小结

一. 介绍

Low-density parity-check，简称LDPC码，翻译为低密度奇偶校验码。

我们所熟悉的LDPC码就是一个典型的线性分组码（linear block code）。在接下来的讨论中，我们将主要关注二进制的线性分组码，也会简称为线性码。

看完本文章，你将学会对偶码（dual code），陪集码（coset），线性分组码。这些都是网络安全编码领域常用的概念。

二. 线性分组码

假定某二进制线性分组码的输出的比特长度为n-k，输出长度为n，那么该线性编码通常写做：

(n,n-k)

建议将此处的比特序列理解成向量，以方便后续的理解。

因为二进制每个元素均只能取0或1，那么就属于有限域GF(2)内，通常写做：

$C\subseteq GF(2)^n$

右上角的n可以理解为比特长度，也可以理解为向量维度。

很明显该码字的基数：

$|C|=2^{n-k}$

码字就是我们通常所说的codewords。

编码之前的元素叫消息，比特长度为n-k，其空间大小如下：

$GF(2)^{n-k}$

编码之和称之为码字，其比特长度为n，空间大小为：

$GF(2)^n$

编码的过程其实就是一种双射（bijective mapping）的过程。

编码的速率定义为输入长度除以输出长度，也就是：

$R=\frac{n-k}{n}$

三. 生成矩阵

generator matrix，生成矩阵，通常简写为G

一个线性码C可以利用生成矩阵来完整表示，生成矩阵的维度如下：

$G\in GF(2)^{{n-k}\times n}$

那么我们就可以直接拿生成矩阵乘以输入的序列，便可以得到输出的序列，也就是完成了线性编码的过程：

右边输入的m为(n-k)行1列（看成列向量）

右边 $G^T$ 为n行n-k列

右边便可以计算输出的左边的m为n行1列（看成列向量）

借助格理论很容易得到，可以把矩阵G的每一行看成该码字的基底（basis）。

通过以上讨论，我们发现，利用生成矩阵即可以把码字完整的表达清楚。当然码字不唯一，当生成矩阵在改变的时候，也就是编码算法在变化。

四. 对偶编码

原来的线性编码C，我们写做(n,n-k）,其对偶的编码通常定义为如下：

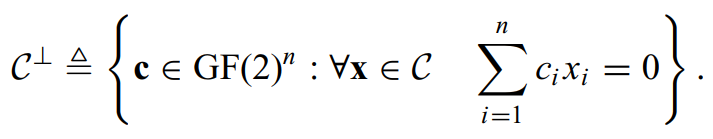
对偶编码的输出长度也为n，否则向量无法完成相乘。一定要要注意此定义要求的任意性。

如果用向量的观点，那么对偶编码 $C^\bot$ 包含所有跟原编码C垂直的向量，而且维度为n维，也就是向量属于：

$GF(2)^n$

五. 校验矩阵

parity-check matrix翻译为校验矩阵

根据以上的讨论，很容易证明对偶编码 $C^\bot$ 为(n,k)的线性码，也就是输入长度为k，输出长度为n。那么很容易得到对偶编码 $C^\bot$ 的生成矩阵可以记为H，如下：

$H\in GF(2)^{k\times n}$

该矩阵也被称之为编码C的校验矩阵。

根据定义校验矩阵和生成矩阵满足：

$GH^T=0$

对于任意的码字x，校验矩阵的理解就是：

$Hx=0$

六. 陪集编码

假定编码C的格式为(n,n-k)，将其校验矩阵记为H，将上式子中的0改为s，格式如下：

$s\in GF(2)^k$

那么可以得到新的编码，如下：

上式子中的s通常称之为特征，syndrome。很明显当s=0时，就是原来的码字，也就是C=C(0)

我们还可以换个角度来理解陪集编码（coset code）。

比如x'满足如下：

Hx'=s

其中x'的格式满足：

$x'\in GF(2)^n$

那么陪集编码则可以理解为原编码相加的格式，如下：

来引入一个新的定义。从以上陪集编码中选择一个x'，如果x'的汉明重量最小的话，那么就称之为coset leader。

假定原编码的格式为(n,n-k)，那么容易证明其有 $2^k$ 个不相交的陪集，对原始空间 $GF(2)^n$ 进行了分割。

七. 小结

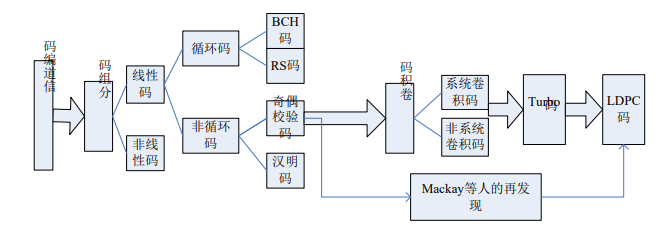
可以看到，信道编码的发展可以简单的归纳为分组码---卷积码-----分组码这样一个过程（在这里按其结构将 Turbo 码也归入卷积码的范畴）。其中 Turbo 码的出现以及迭代译码的思想引入使得信道编解码产生了前所未有的飞跃，但 Turbo 码之后卷积码却没有更大的发展，究其原因就是其没有完备的理论基础，使得人们不能给出其性能上严密的数学解释。

于是在那之后，Mackay等人再次发掘了 Gallager 于 1962 年提出的一种具有稀疏校验矩阵的分组纠错码，即 LDPC 码。LDPC 码和传统的分组码最大的区别在于它们的译码。分组码通常是用最大似然译码，因此，码长一般较短，并用代数方法设计使得复杂度较低。而 LDPC 码是迭代译码，校验矩阵用 Tanner 图表示，码长更长、围绕着校验矩阵 H 的特性进行设计是核心。LDPC 码自身的矩阵结构引入了交织特性，而且其采用迭代译码的方法，使其性能比以往的线性分组码有很大程度的提高。由于其基本原理是基于最原始的线性分组码，因此它有强大的数学工具作为其理论依据，几乎融图论、组合数学、概率论、矩阵论、代数、几何、代数数论、黎曼几何于一炉。

在通信，网络安全等领域，我们很难再找到某个方向可以有如此深厚的理论基础与之媲美。但理论上的完备性并不能使其直接应用于实际，因此从码字构造的方向来说，如何将 LDPC 码应用于实际工作才是值得深入研究的。为了保证其实现性，性能上就要有所妥协。在编码方面，以准循环 LDCP 码，即 QC-LDPC 码为例，为了降低硬件上的存储空间以及易于编码，就要以牺牲 LDPC 码先天的优势——交织特性为代价，这样便做出了性能与实现上的折中。但这种折中是有意义的，为 LDPC 码的实际应用开辟了道路。而且，通过某些方法，可以使设计出的码字在易于存储实现的同时，还能保证一定的性能。在译码方面，种种方法都可以归结为和积算法（SPA）的变形，都是在其基础上做出改进，从而保证译码性能前提下使译码器尽可能的简单。相对于 Turbo 码，LDPC 码的解码迭代次数还是过高，这样在实际应用中的竞争力便大打折扣。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1406785.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！