树(Tree)

知识框架

树的定义

树和图一样都是非线性结构，树是n个结点的有限集合，当n=0时，称这棵树为空树。 非空树有以下特征：

• 有且仅有一个称为根的结点。
• 如果n>1, 除根结点以外其它结点可以分为m(m>0)个不相交的集合T1,T2,T3,T4,…,Tm，其中每一个集合都是一棵树。树T1, T2, T3,…,Tm称为这棵对的子树。

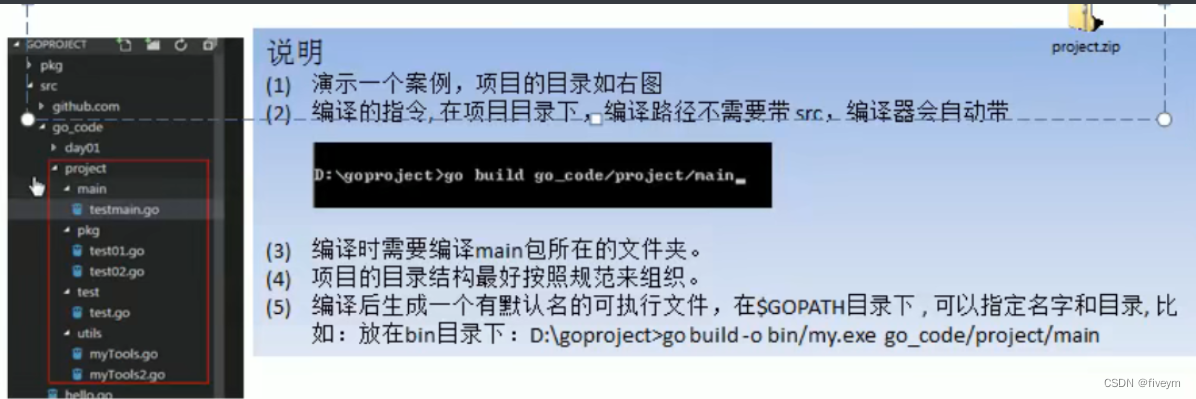
下图是一棵普通的树

树的相关术语

• 节点：树是由有限个元素组成的集合，每人元素都称作一个节点，上图A、B、 C、 D、 E、 F、G、H、I等都是树的节点;
• 节点的度：一个节点含有的子树的个数称为该节点的度;
• 叶节点或终端节点：度为0的节点称为叶节点，D,E,C,G都是叶节点;
• 非终端节点或分支节点：度不为0的节点;
• 子节点(孩子节点): 一个节点含有的子树的根节点称为该节点的子节点;
• 父节点(双亲节点)：若一个节点含有子节点，则这个节点称为其子节点的父节点;
• 兄弟节点：具有相同父节点的节点互称为兄弟节点;
• 堂兄弟节点：双亲在同一层的节点互为堂兄弟;
• 节点的祖先：从根到该节点所经分支上的所有节点;
• 子孙节点：以某节点为根的子树中任一节点都称为该节点的子孙;
• 森林：由m（m>=0）棵互不相交的树的集合称为森林;
• 树的度：一棵树中，最大的节点的度称为树的度;
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推;
• 树的高度或深度：树中节点的最大层次;

树的分类

• 有序树：树的各个子树的顺序是固定的，不能随意改变顺序。
• 无序树：树的各个子树的顺序可变。
• 二叉树: 每个节点最多只能有两个子节点的树称为二叉树，二叉树是有序树，左右子树的顺序不能改变。二叉树又可以分为满二叉树和完全二叉树。
• B树
• 霍夫曼树

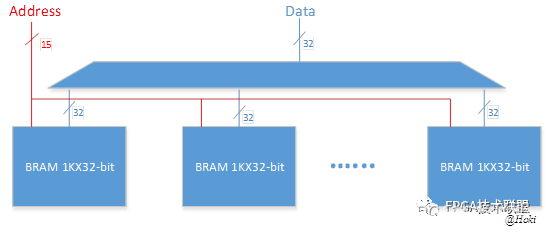
树的存储结构

计算机的内存是线性的, 而树是非线性的数据结构,如何将非线性的树状结构在线性的内存中存储起来,这是一个值得探讨的问题。目前主要有以下几种存储方式：

双亲表示法

• 实现:通常用一个二维数组，在存储结点的同时也将对应节点的父节点存储进来。
• 特点：找父节点容易、找子节点难。

孩子表示法

• 实现：每个结点都存储在一个二维数组的第一列里面，多个子节点之间以链表方式连接，最后一个子节点的指向为NULL，数组的第二个元素指向其子节点链表的起始地址。
• 特点：找子节点容易，找父节点难。

双亲孩子表示法

• 实现：将双亲表示法与孩子表示法综合起来，既存储父节点的下标，又指向子节点链表。
• 特征：找父节点与子节点都比较方便，但相对前面两种复杂度有一定程度的提升。

二叉树存储

• 二叉树存储就是将普通的树转换成二叉树后再进行存储，二叉树的存储将另作讨论。
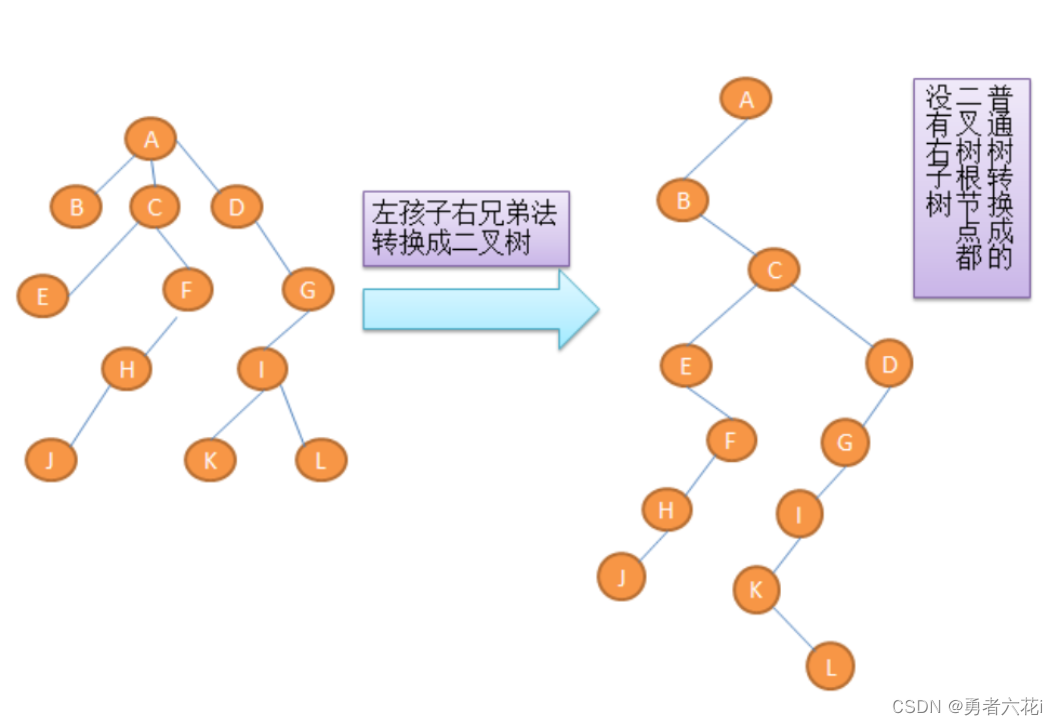
• 将普通树转换成二叉树有一个方法，左孩子右兄弟法，就是说从根节点开始，每个节点的左子节点存储它的一个孩子，右子节点存储它的一个兄弟，如下图所示：