【数据结构】二叉树算法讲解（定义+算法原理+源码）

博主介绍：✌全网粉丝喜爱+、前后端领域优质创作者、本质互联网精神、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战✌有需要可以联系作者我哦！

🍅附上相关C语言版源码讲解🍅

👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟

一、二叉树定义（特点+结构）

二叉树算法性质：

二、算法实现（完整代码）

三、算法总结

二叉树的优点：

二叉树的缺点：

二叉树的应用：

小结

大家点赞、收藏、关注、评论啦！

谢谢哦！如果不懂，欢迎大家下方讨论学习哦。

一、二叉树定义（特点+结构）

二叉树是一种树形结构，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树具有以下定义和特点：

1. 节点：二叉树是由节点构成的集合。每个节点包含三个基本信息：
- 数据元素（或称为节点值）。
- 指向左子节点的指针/引用。
- 指向右子节点的指针/引用。

2. 根节点：二叉树中的一个节点被称为根节点，它是整个树的起始节点。一棵二叉树只有一个根节点。

3. 叶子节点：没有子节点的节点被称为叶子节点（或叶节点）。

4. 父节点和子节点：每个节点都有一个父节点，除了根节点。父节点指向它的子节点。

5. 深度：一个节点的深度是从根节点到该节点的唯一路径的边的数量。根节点的深度为0。

6. 高度/深度：一棵二叉树的高度（或深度）是树中任意节点的最大深度。

7. 子树：二叉树中的任意节点和它的所有子孙节点组成的集合被称为子树。

8. 二叉搜索树（BST）：在二叉搜索树中，每个节点的左子树中的节点值都小于该节点的值，而右子树中的节点值都大于该节点的值。

9. 满二叉树：如果一棵深度为k，且有2^k - 1个节点的二叉树被称为满二叉树。

10. 完全二叉树：对于一棵深度为k的二叉树，除了最后一层外，其它各层的节点数都达到最大值，且最后一层的节点都集中在左边，被称为完全二叉树。

二叉树的定义为：

struct TreeNode {
    int val;                 // 节点值
    TreeNode *left;          // 左子节点指针
    TreeNode *right;         // 右子节点指针
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

上述定义为C++中使用类实现的二叉树节点定义，包含节点值、左子节点指针和右子节点指针。

二叉树算法性质：

你提到的这些性质描述了二叉搜索树（Binary Search Tree，BST）的一些重要特征。让我们逐一解释这些性质：

1. 将任何一个点看作Root节点，则这个点的左子树也是 Binary Search Tree：这表示二叉搜索树中每个节点的左子树都满足二叉搜索树的性质，即左子树上的节点值小于当前节点的值。

2. 将任何一个点看作Root节点，则这个点的右子树也是 Binary Search Tree：类似地，这表明每个节点的右子树都是一个二叉搜索树，右子树上的节点值大于当前节点的值。

3. Binary Search Tree中的最小节点，一定是整棵树中最左下的叶子节点：这是因为最小节点不会有左子节点，只能一直沿着左子树往下走，直到叶子节点。

4. Binary Search Tree中的最大节点，一定是整棵树中最右下的叶子节点：同样，最大节点不会有右子节点，只能一直沿着右子树往下走，直到叶子节点。

这些性质是二叉搜索树在节点排列和结构上的特点，它们使得在二叉搜索树上执行搜索、插入和删除等操作更加高效。通过遵循这些性质，可以确保在整个树结构中维持有序性，使得二叉搜索树成为一种常用的数据结构。

二、算法实现（完整代码）

通过二叉树实现A、B、C、D的简单应用

#include<iostream>
using namespace std;
typedef char DataType;
struct BiNode
{
	DataType data;
	BiNode *lchild,*rchild;
};
//（1）假设二叉树采用链接存储方式存储，分别编写一个二叉树先序遍历的递归
//算法和非递归算法。
class BiTree
{
	public:
		BiTree(){root=Create(root);}//构造函数，建立一颗二叉树
		~BiTree(){Release(root);}//析构函数，释放各个节点的存储空间
		void Preorder(){Preorder(root);}//前序遍历二叉树
		void Inorder(){Inorder(root);}//中序遍历二叉树
		void Postorder(){Postorder(root);}//后序遍历二叉树
		void Levelorder(){Levelorder(root);};//层序遍历二叉树
	private:
		BiNode *root;//指向根节点的头指针
		BiNode *Create(BiNode *bt);//构造函数调用
		void Release(BiNode *bt);//析构函数调用
		void Preorder(BiNode *bt);//前序遍历函数调用
		void Inorder(BiNode *bt);//中序遍历函数调用
		void Postorder(BiNode *bt);//后序遍历函数调用
		void Levelorder(BiNode *bt);//层序遍历函数调用
};
//前序遍历
void BiTree::Preorder(BiNode *bt)
{
	if(bt==NULL)return;//递归调用的结束条件
	else{
		cout<<bt->data<<" ";//访问根节点bt的数据域
		Preorder(bt->lchild);//前序递归遍历bt的左子树
		Preorder(bt->rchild);//前序递归遍历bt的右子树
	}
}
//中序遍历
void BiTree::Inorder(BiNode *bt)
{
	if(bt==NULL)return;//递归调用的结束条件
	else{
		Inorder(bt->lchild);//中序递归遍历bt的左子树
		cout<<bt->data<<" ";//访问根节点的数据域
		Inorder(bt->rchild);//中序递归遍历bt的右子树
	}
}
//后序遍历
void BiTree::Postorder(BiNode *bt)
{
	if(bt==NULL)return;//递归调用的结束条件
	else{
		Postorder(bt->lchild);//后序递归遍历bt的左子树
		Postorder(bt->rchild);//后序递归遍历bt的右子树
		cout<<bt->data<<" ";//访问根节点bt的数据域
	}
}
//层序遍历
void BiTree::Levelorder(BiNode *bt){
	BiNode *Q[100],*q=NULL;
	int front=-1,rear=-1;//队列初始化 
	if(root == NULL) return;//二叉树为空，算法结束
	Q[++rear]=root;//根指针入队
	while(front!=rear){//当队列非空时 
		q=Q[++front];//出队
		cout<<q->data<<" ";
		if(q->lchild!=NULL) Q[++rear]=q->lchild;
		if(q->rchild!=NULL) Q[++rear]=q->rchild; 
	} 
}
//创建二叉树 
BiNode *BiTree::Create(BiNode *bt)
{
	static int i=0;
	char ch;
	string str="AB#D##C##";
	ch=str[i++];
	if(ch=='#')bt=NULL;//建立一棵空树 
	else {
		bt=new BiNode;bt->data=ch;//生成一个结点，数据域为ch
		bt->lchild=Create(bt->lchild);//递归建立左子树
		bt->rchild=Create(bt->rchild);//递归建立右子树
	}
	return bt;
}
//销毁二叉树 
void BiTree::Release(BiNode *bt)
{
	if(bt!=NULL){
		Release(bt->lchild);
		Release(bt->rchild);
		delete bt;
	}
}
int main()
{
	cout<<"创建一棵二叉树"<<endl;
	BiTree T;//创建一颗二叉树
	cout<<"---层序遍历---"<<endl;//A B C D 
	T.Levelorder();
	cout<<endl;
	cout<<"---前序遍历---"<<endl;//A B D C
	T.Preorder();
	cout<<endl;
	cout<<"---中序遍历---"<<endl;//B D A C
	T.Inorder();
	cout<<endl;
	cout<<"---后序遍历---"<<endl;//D B C A
	T.Postorder();
	cout<<endl;
	return 0;
}

执行结果：

序存储的完全二叉树递归先序遍历算法描述（C++）如下：

//完全二叉树的顺序存储结构
#include <iostream>
#include <string.h>
#define MaxSize 100
using namespace std;
typedef char DataType;
class Tree{
	public:
		Tree(string str);//构造函数
		void createTree();//创建二叉树 
		void seqPreorder(int i);//先序遍历二叉树 
		void seqInorder(int i);//中序遍历二叉树 
		void seqPostorder(int i);//后序遍历二叉树 
	private: 
		DataType node[MaxSize];//结点中的数据元素
		int num=0;//二叉树结点个数 
		string str;
};
 
Tree::Tree(string str){
	this->str = str;
} 
 
void Tree::createTree(){
	for(int i = 1;i < str.length()+1 ;i++){
		node[i]=str[i-1];
		num++;
	}
	node[0] = (char)num;
}
 
//顺序存储的完全二叉树递归先序遍历算法描述（C++）如下：
void Tree::seqPreorder(int i){
	if(i==0)//递归调用的结束条件
		return;
	else{
		cout<<"  "<<(char)node[i];//输出根结点
		if(2*i<=(char)node[0])
			seqPreorder(2*i);//先序遍历i的左子树
		else
			seqPreorder(0);
		if(2*i+1<=(char)node[0])
			seqPreorder(2*i+1);//先序遍历i的右子树
		else
			seqPreorder(0); 
	} 
} 
 
//顺序存储的完全二叉树递归中序遍历算法描述（C++）如下：
void Tree::seqInorder(int i){
	if(i==0)//递归调用的结束条件
		return;
	else{
		if(2*i<=(char)node[0])
			seqInorder(2*i);//中序遍历i的左子树
		else
			seqInorder(0);
		cout<<"  "<<(char)node[i];//输出根结点
		if(2*i+1<=(char)node[0])
			seqInorder(2*i+1);//中序遍历i的右子树
		else
			seqInorder(0); 
	} 
} 
 
//顺序存储的完全二叉树递归后序遍历算法描述（C++）如下：
void Tree::seqPostorder(int i){
	if(i==0)//递归调用的结束条件
		return;
	else{
		if(2*i<=(char)node[0])
			seqPostorder(2*i);//后序遍历i的左子树
		else
			seqPostorder(0);
		if(2*i+1<=(char)node[0])
			seqPostorder(2*i+1);//后序遍历i的右子树
		else
			seqPostorder(0); 
		cout<<"  "<<(char)node[i];//输出根结点
	} 
} 
 
// （2）一棵完全二叉树以顺序方式存储，设计一个递归算法，对该完全二叉树进
//行中序遍历。
int main(){
	string str = "ABCDEFGHIJ";
	Tree T(str);//定义对象变量bus
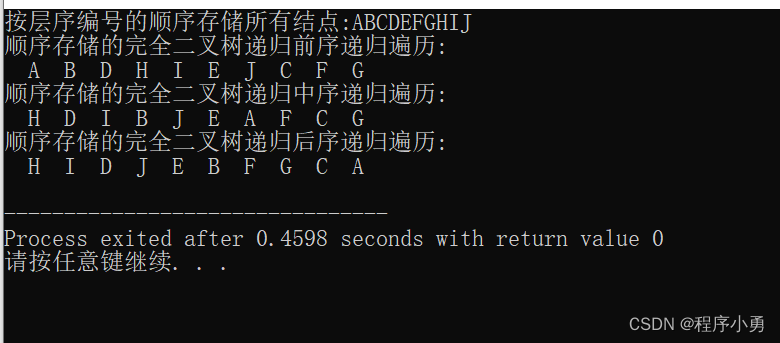
	cout<<"按层序编号的顺序存储所有结点:"<<str<<endl;
	T.createTree();
	cout<<"顺序存储的完全二叉树递归前序递归遍历:"<<endl; 
	T.seqPreorder(1);
	cout<<endl; 
	cout<<"顺序存储的完全二叉树递归中序递归遍历:"<<endl; 
	T.seqInorder(1);
	cout<<endl; 
	cout<<"顺序存储的完全二叉树递归后序递归遍历:"<<endl; 
	T.seqPostorder(1);
	cout<<endl; 
	return 0;
}