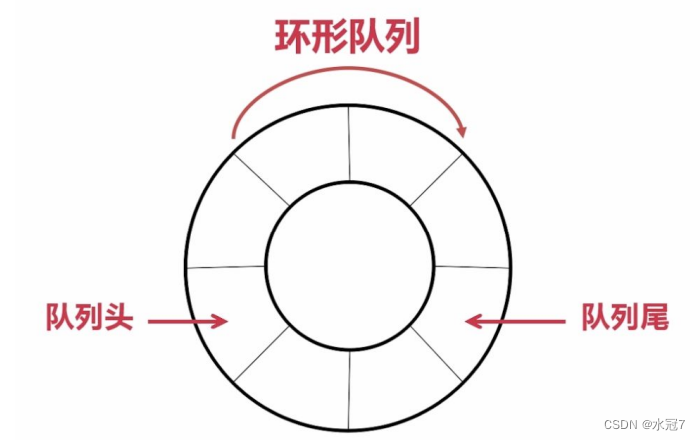
光伏发电

一、问题分析（完整资料在文末）

问题一：

首先题目要求得到电能行业与经济状况、居民消费水平、城市化率和市场化程度等因素的关系，并对供电量进行预测。其中，电能采用供电量数据、经济采用GDP数据，消费水平采用居民收入水平或消费水平数据，市场化采用中国市场化综合指标，再加上城市化率数据，进行相关性分析得到对应关系整体来看，分关系判断和预测两个部分，一是使用相关性分析、差异性分析等方法来判断因素之间的联系程度，包括皮尔逊分析、斯皮尔曼分析等。二是使用时间序列预测模型， 对供电量采用LSTM、ARIMA等模型对时间数据进行预测得到结果。但是供电量受其他因素影响，因此需要添加一定的突发性波动或是非线性规律，也可以采用BP神经网络等进行预测。

问题二：

首先题目询问是否具有可行性，明确讨论可行性也就是看有没有收益。可以建立综合评价模型对多项指标进行统一评价，包括熵权法、层次分析法、主成分分析法等，本文采用熵权法。同时也可以从投资回报率、回报时间角度看。成本包括固定成本和每一次的维修成本（一般来说会换算成一个固定价格），本文将数据量化为整体投入成本，地理数据则可以采用非耕地面积、位置坡度、距离城镇的距离等，光照条件可以采用太阳光辐射强度和平均光照时间，此外还可以考虑不同地区光伏发电的价格，光伏板容量，系统效率等，作为新的评价指标。

问题三:

对于问题三，我们需要计算出目前中国光伏发电的最大潜力即计算出中国光伏发电的年最大发电量。为了求得最大发电量，我们建立了基于基于粒子群算法的动态规划模型的优化模型。首先，我们收集中国的电力数据全国电力数据包括二十年来太阳能电池（光伏电池）产量、总能源结构比例、平均系统价格、年度投资、太阳辐射量、光伏板成本、安装成本、运营维护、成本电价、电网接入成本、电网容量数据。我们将光伏发电量最大值作为目标函数，引入开关变量，将光伏发电本身作为决策变量。通过分析上述数据，得到各数据间的相关性，构建约束条件。 为了提高准确性和寻优的速度，我们选择粒子群算法进行寻优。

对于问题四，我们从政策中了解到，如果在2060年实现碳中和目标，电力行业单位供电碳排放要从目前的600克左右，要以每年10克左右的速度往下降，换个指标来说，需要把煤电装机比重控制在10%以下，2060年可再生能源发电装机比重至少达到80%以上。因此，我们搜集出中国电力结构的各项数据，采用灰度预测的方式来判断指标是否达到，最后结合光伏发展规划来补充说明。

三、模型假设

• 假设中国在未来几十年内经济持续稳定增长，电力行业稳步推进。
• 假设中国政府继续实施光伏发电等可再生能源的优惠与补贴政策。
• 假设中国的土地和其他自然资源对光伏发电的发展有一定的限制作用，需要在资源有限的情况下进行优化配置。

四、符号说明

符号	定义

五、模型的建立与求解

5.1问题一模型的建立与求解

5.1.1基于箱线图的数据预处理

首先对数据进行预处理（可以说明一下我们选择的数据类型），包括缺失值和异常值的剔除与替换。可以使用箱线图法。

当数据中出现异常值，尤其是存在着偏离较大的离群点时，会对数据分析与模型建立带来误差。因此必须对异常值进行检测与剔除。常用的异常值检测方法包括3σ法则、Z分布方法和箱线图法。其中，3σ法则和Z分布方法是以正态分布为假设前提的，而箱线图法[2]对数据分布没有要求。由于本文的数值分布不均匀，不符合正态分布特性。故选择使用对数据分布没有要求的箱线图，对数值型特性进行异常值检测。

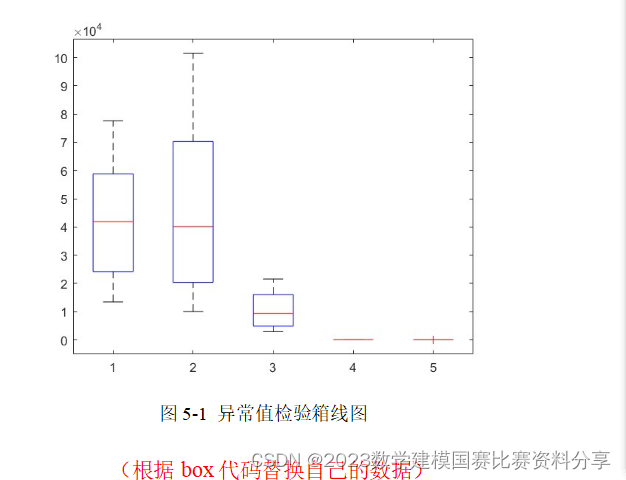
使用箱线图对数据进行异常值检测的原理为：通过计算四分位数加减1.5倍四分位距，即是计算Q1－1.5IQR和Q3+1.5IQR的值，规定落在这一区间之外的数据为异常点。在箱线图中，可以看出变量数据的中位数、上四分位数、下四分位数、上下边缘和潜在异常点。本文通过使用上四分位数代替数值大于 Q3+1.5IQR 的数据，使用下四分位数代替数值小于Q1－1.5IQR的数据，并绘制出了异常值的箱线图，如图5-1所示。

在图5-1中，中间线表示中位数，箱子的上下边缘分别表示上四分位数和下四分位数，图中上方和下方的横线表示上下边缘，最上方和最下方的点为潜在离群值。从图中可以看出，婚姻状况、妊娠时间以及整晚睡眠时间这三个数据的异常值较多，而教育程度、分娩方式、CBTS等异常值相对较少，说明数据离群值较少，数据质量相对较好。

5.1.2描述性统计分析

为更好地分析电力供应与多种因素相互影响关系，本文对直方图分析，如图5-2所示，可直观地体现各变量在不同取值的分布情况。

点击链接加入群聊【2024华数杯数学建模】：