JoyRL Actor-Critic算法

策略梯度算法的缺点

这里策略梯度算法特指蒙特卡洛策略梯度算法，即 REINFORCE 算法。相比于 DQN 之类的基于价值的算法，策略梯度算法有以下优点。

适配连续动作空间。在将策略函数设计的时候我们已经展开过，这里不再赘述。
适配随机策略。由于策略梯度算法是基于策略函数的，因此可以适配随机策略，而基于价值的算法则需要一个确定的策略。此外其计算出来的策略梯度是无偏的，而基于价值的算法则是有偏的。

但同样的，策略梯度算法也有其缺点。

采样效率低。由于使用的是蒙特卡洛估计，与基于价值算法的时序差分估计相比其采样速度必然是要慢很多的，这个问题在前面相关章节中也提到过。
高方差。虽然跟基于价值的算法一样都会导致高方差，但是策略梯度算法通常是在估计梯度时蒙特卡洛采样引起的高方差，这样的方差甚至比基于价值的算法还要高。
收敛性差。容易陷入局部最优，策略梯度方法并不保证全局最优解，因为它们可能会陷入局部最优点。策略空间可能非常复杂，存在多个局部最优点，因此算法可能会在局部最优点附近停滞。
难以处理高维离散动作空间：对于离散动作空间，采样的效率可能会受到限制，因为对每个动作的采样都需要计算一次策略。当动作空间非常大时，这可能会导致计算成本的急剧增加。

结合了策略梯度和值函数的 Actor-Critic 算法则能同时兼顾两者的优点，并且甚至能缓解两种方法都很难解决的高方差问题。

Q：为什么各自都有高方差的问题，结合了之后反而缓解了这个问题呢？

A：策略梯度算法是因为直接对策略参数化，相当于既要利用策略去与环境交互采样，又要利用采样去估计策略梯度，而基于价值的算法也是需要与环境交互采样来估计值函数的，因此也会有高方差的问题。

而结合之后呢，Actor 部分还是负责估计策略梯度和采样，但 Critic 即原来的值函数部分就不需要采样而只负责估计值函数了，并且由于它估计的值函数指的是策略函数的值，相当于带来了一个更稳定的估计，来指导 Actor 的更新，反而能够缓解策略梯度估计带来的方差。

Q Actor-Critic算法

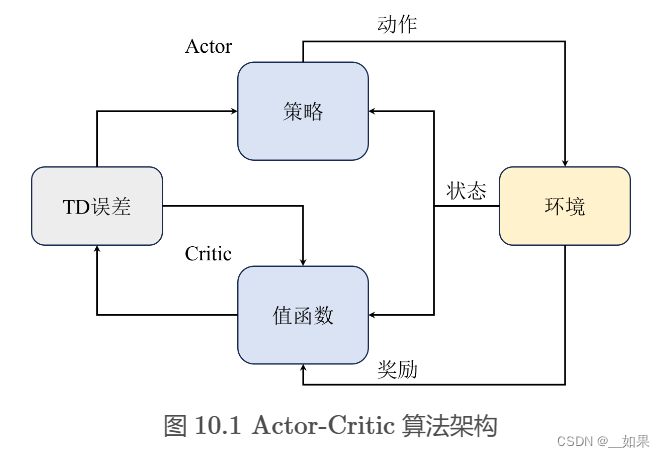
如图 10.1 所示，我们通常将 Actor 和 Critic 分别用两个模块来表示，即图中的策略函数（ Policy ）和价值函数（ Value Function ）。Actor与环境交互采样，然后将采样的轨迹输入 Critic 网络，Critic 网络估计出当前状态-动作对的价值，然后再将这个价值作为 Actor 网络的梯度更新的依据，这也是所有 Actor-Critic 算法的基本通用架构

A2C与A3C算法

A2C

A3C

广义优势估计

由于优势函数通本质上来说还是使用蒙特卡洛估计，因此尽管减去了基线，有时候还是会产生高方差，从而导致训练过程不稳定

实战：A2C算法

定义模型

Critic 的输入是状态，输出则是一个维度的价值，而 Actor 输入的也会状态，但输出的是概率分布

class Critic(nn.Module):
    def __init__(self,state_dim):
        self.fc1 = nn.Linear(state_dim, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, 1)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        value = self.fc3(x)
        return value

class Actor(nn.Module):
    def __init__(self, state_dim, action_dim):
        self.fc1 = nn.Linear(state_dim, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, action_dim)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        logits_p = F.softmax(self.fc3(x), dim=1)
        return logits_p

这里由于是离散的动作空间，根据在策略梯度章节中设计的策略函数，我们使用了 softmax 函数来输出概率分布。另外，实践上来看，由于 Actor 和 Critic 的输入是一样的，因此我们可以将两个网络合并成一个网络，以便于加速训练。这有点类似于 Duelling DQN 算法中的做法

class ActorCritic(nn.Module):
    def __init__(self, state_dim, action_dim):
        self.fc1 = nn.Linear(state_dim, 256)
        self.fc2 = nn.Linear(256, 256)
        self.action_layer = nn.Linear(256, action_dim)
        self.value_layer = nn.Linear(256, 1)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        logits_p = F.softmax(self.action_layer(x), dim=1)
        value = self.value_layer(x)
        return logits_p, value

动作采样

与 DQN 算法不同等确定性策略不同，A2C 的动作输出不再是 Q 值最大对应的动作，而是从概率分布中采样动作，这意味着即使是很小的概率，也有可能被采样到，这样就能保证探索性

# Categorical分布函数，能直接从概率分布中采样动作
from torch.distributions import Categorical
class Agent:
    def __init__(self):
        self.model = ActorCritic(state_dim, action_dim)
    def sample_action(self,state):
        '''动作采样函数
        '''
        state = torch.tensor(state, device=self.device, dtype=torch.float32)
        logits_p, value = self.model(state)
        dist = Categorical(logits_p) 
        action = dist.sample() 
        return action

策略更新

我们首先需要计算出优势函数，一般先计算出回报，然后减去网络输出的值即可

class Agent:
    # 定义一个Agent类

    def _compute_returns(self, rewards, dones):
        # 计算回报
        returns = []  # 初始化一个回报列表
        discounted_sum = 0  # 初始化折扣累计和
        # 从后向前遍历奖励和是否结束的序列
        for reward, done in zip(reversed(rewards), reversed(dones)):
            # 如果游戏结束，则折扣累计和重置为0
            if done:
                discounted_sum = 0
            # 否则，将奖励加上折现因子gamma乘以之前的折扣累计和
            discounted_sum = reward + (self.gamma * discounted_sum)
            # 将计算出的折扣累计和添加到回报列表的开头
            returns.insert(0, discounted_sum)
        # 将回报列表转换为PyTorch张量，并移到Agent指定的设备上
        returns = torch.tensor(returns, device=self.device, dtype=torch.float32).unsqueeze(dim=1)
        # 对回报进行归一化处理
        returns = (returns - returns.mean()) / (returns.std() + 1e-5)  # 添加一个很小的数以避免除以零
        return returns

    def compute_advantage(self):
        '''计算优势函数
        '''
        # 从记忆库中随机抽取一批经验
        logits_p, states, rewards, dones = self.memory.sample()
        # 计算回报
        returns = self._compute_returns(rewards, dones)
        # 将状态转换为PyTorch张量，并移到Agent指定的设备上
        states = torch.tensor(states, device=self.device, dtype=torch.float32)
        # 前向传播模型以获得动作的概率和对数概率
        logits_p, values = self.model(states)
        # 计算优势，即回报与批评价值的差
        advantages = returns - values
        return advantages

这里我们使用了一个技巧，即将回报归一化，这样可以让优势函数的值域在 [−1,1] 之间，这样可以让优势函数更稳定，从而减少方差。计算优势之后就可以分别计算 Actor 和 Critic 的损失函数了

class Agent:
    def compute_loss(self):
        '''计算损失函数
        '''
        logits_p, states, rewards, dones = self.memory.sample()
        returns = self._compute_returns(rewards, dones)
        states = torch.tensor(states, device=self.device, dtype=torch.float32)
        logits_p, values = self.model(states)
        advantages = returns - values
        dist = Categorical(logits_p)
        log_probs = dist.log_prob(actions)
        # 注意这里策略损失反向传播时不需要优化优势函数，因此需要将其 detach 掉
        actor_loss = -(log_probs * advantages.detach()).mean() 
        critic_loss = advantages.pow(2).mean()
        return actor_loss, critic_loss