所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

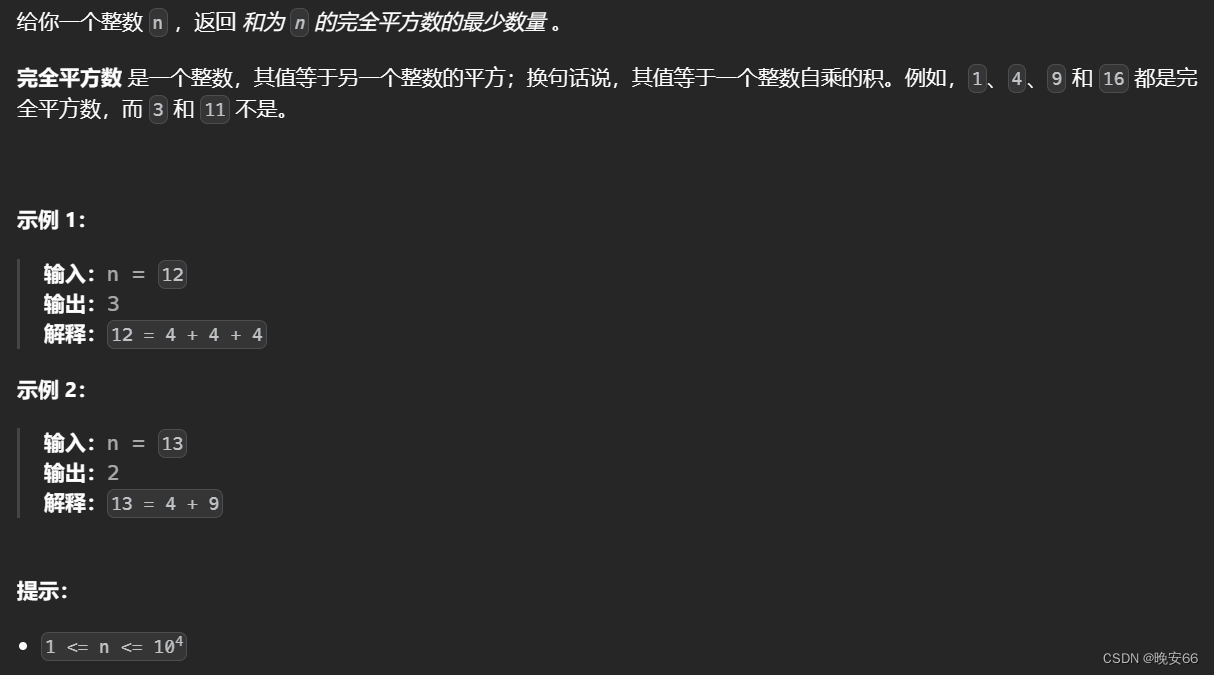
一、题目

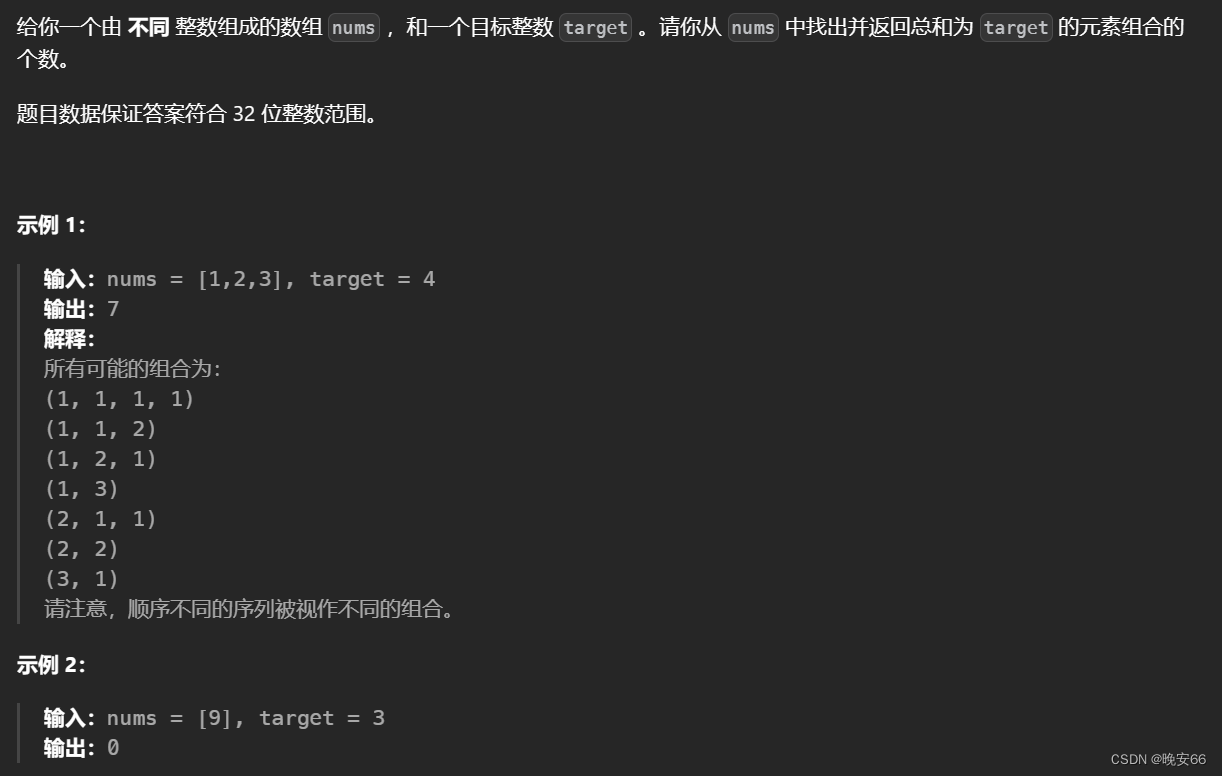
二、解法

  思路分析：本题明面上说是组合，实际上指的是排列。动态规划排列组合背包问题需要考虑遍历顺序。$dp[i]$指的是nums数组中总和为target的元素排列的个数。$dp[i]$可以由$dp[i-nums[j]]$推导出来。因此递推公式为$dp[i]+=dp[i-nums[j]]$。$dp[0]$初始化为1，其他元素初始化为0。因为是排列问题，排列问题需要先遍历背包容量，后遍历物品。如果把遍历nums（物品）放在外循环，遍历target的作为内循环的话，举一个例子：计算dp[4]的时候，结果集只有 {1,3} 这样的集合，不会有{3,1}这样的集合，因为nums遍历放在外层，3只能出现在1后面。C++测试用例有两个数相加超过int的数据，所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
  程序如下：

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int>dp(target + 1, 0);
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {  // 遍历背包容量
            for (int j = 0; j < nums.size(); j++) {    // 遍历物品
                if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
};

复杂度分析：

• 时间复杂度： $O(target\ast n)$，n是nums数组长度。
• 空间复杂度：$O(target)$。

三、完整代码

# include <iostream>
# include <vector>
using namespace std;

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int>dp(target + 1, 0);
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {  // 遍历背包容量
            for (int j = 0; j < nums.size(); j++) {    // 遍历物品
                if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
};

int main() {
    Solution s1;
    vector<int> nums = { 1,2,3 };
    int target = 4;
    int result = s1.combinationSum4(nums, target);
    cout << result << endl;
    system("pause");
    return 0;
}

end