所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

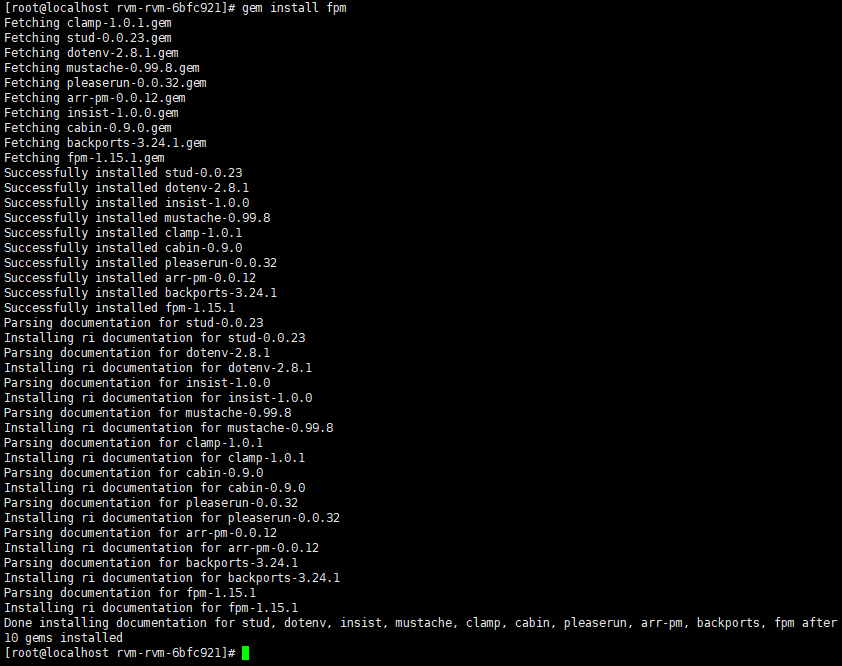
一、题目

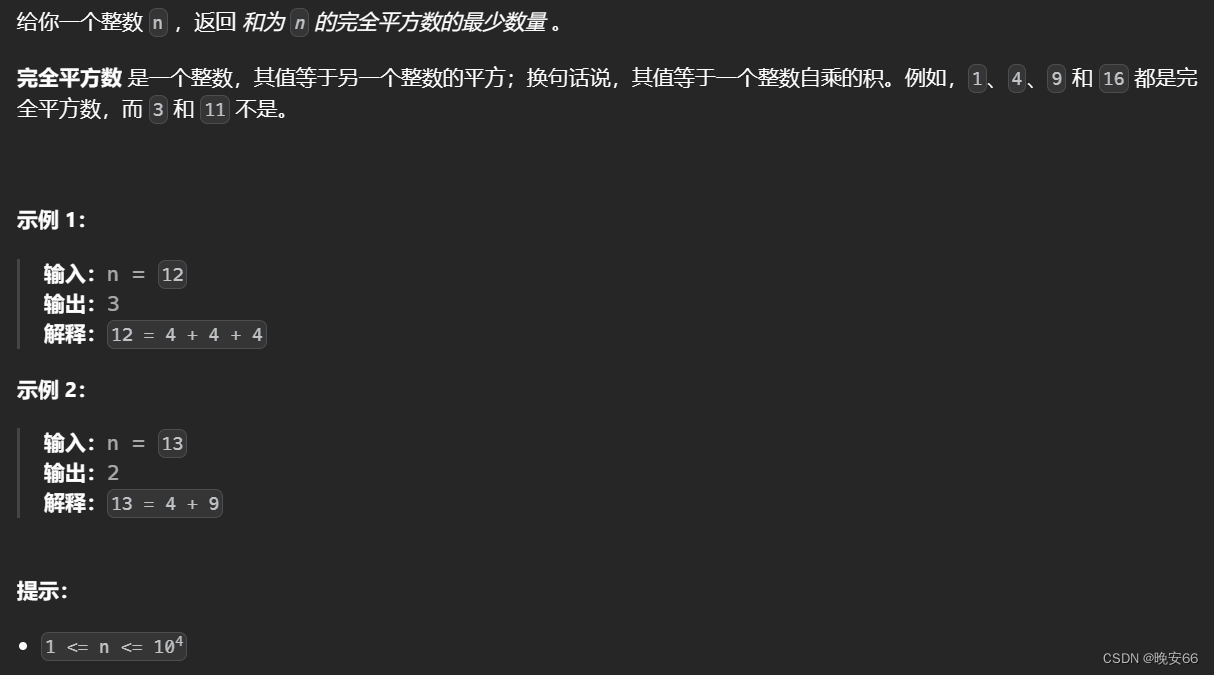
二、解法

  思路分析：本题可以抽象成一个完全背包问题。完全平方数是物品，n为背包最大重量。本题和【算法与数据结构】322、LeetCode零钱兑换的思路基本一样。

• 第一步，$dp[j]$的含义。$dp[j]$代表的是背包容量$j$时，组成背包的最少物品数。
• 第二步，递推公式。$dp[j]$可以由$dp[j-nums[i]]$得出，在此基础上加上1即可。因为要去最小的组合数量，所有最终的递归公式变成$dp[j]=max(dp[j-nums[i]],dp[j])$。
• 第三部，元素初始化。$dp[0]$初始化为0。因为有min函数的关系，动态数组的其他元素初始化应该为int类型的最大整数。
• 第四部，递归顺序。本题无所谓组合和排列问题，所以先遍历物品后遍历背包容量还是先遍历背包容量后遍历物品都可以。
• 第五步，打印结果。最终的dp数组存有所需的完全平方数的最小数量，直接返回。
    程序如下：

class Solution {
public:
	int numSquares(int n) {
		vector<int> dp(n + 1, INT_MAX);
		dp[0] = 0;
		for (int i = 1; i * i <= n; i++) {		// 遍历物品
			for (int j = i * i; j <= n; j++) {	// 遍历背包容量
				if (dp[j - i * i] != INT_MAX) {
					dp[j] = min(dp[j - i * i] + 1, dp[j]);
				}
			}
		}
		return dp[n];
	}
};

复杂度分析：

• 时间复杂度： $O(n\ast \sqrt{n})$。
• 空间复杂度：$O(n)$。

三、完整代码

# include <iostream>
# include <vector>
using namespace std;

class Solution {
public:
	int numSquares(int n) {
		vector<int> dp(n + 1, INT_MAX);
		dp[0] = 0;
		for (int i = 1; i * i <= n; i++) {		// 遍历物品
			for (int j = i * i; j <= n; j++) {	// 遍历背包容量
				if (dp[j - i * i] != INT_MAX) {
					dp[j] = min(dp[j - i * i] + 1, dp[j]);
				}
			}
		}
		return dp[n];
	}
};

int main() {
	Solution s1;
	int n = 13;
	int result = s1.numSquares(n);
	cout << result << endl;
	system("pause");
	return 0;
}

end