every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)是一种用于解决优化问题的元启发式算法。它通过模拟鸟群或鱼群中的行为来进行优化搜索。
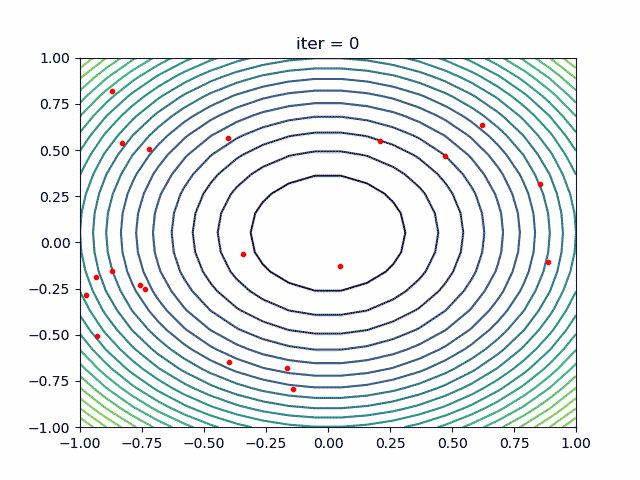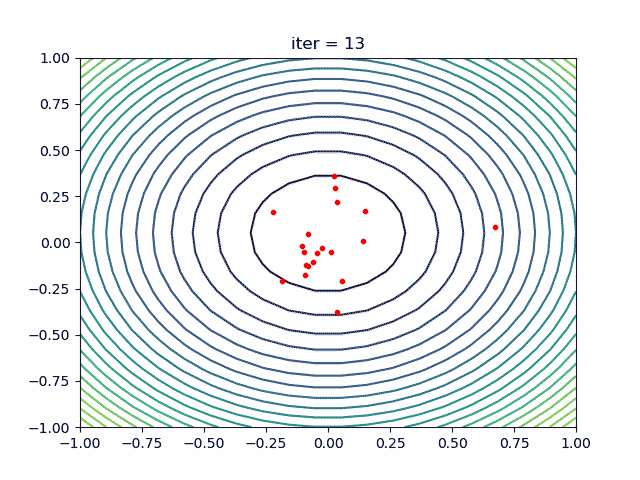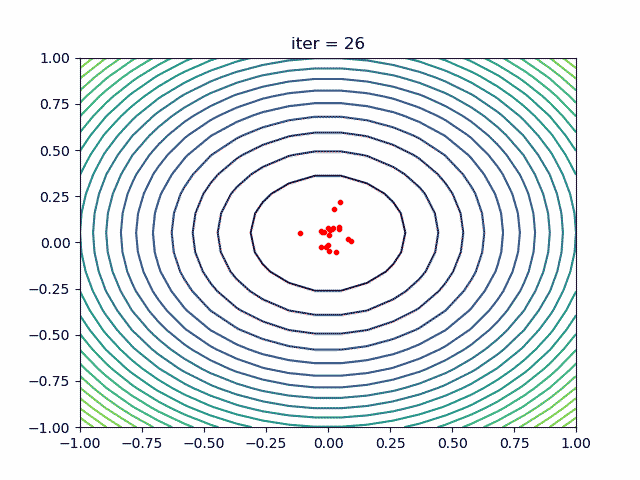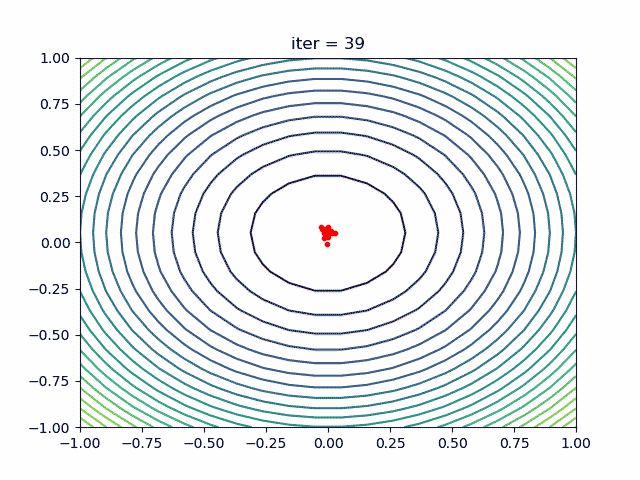
在粒子群算法中,问题的潜在解被表示为一群粒子。每个粒子代表一个候选解,并根据其自身的经验和群体的信息进行移动和调整。粒子的位置表示候选解的特征向量,速度表示粒子在搜索空间中的移动方向和速度。
粒子群算法广泛应用于各种优化问题,如函数优化、神经网络训练、组合优化等。它是一种简单且易于实现的优化算法,具有全局搜索能力和较好的收敛性
1. 简介
1.1 概念
1995年,美国学者Kennedy和Eberhart共同提出了粒子群算法,其基本思想源于对鸟类群体行为进行建模与仿真的研究结果的启发[1]。
是不是也可以叫“鸟群算法”,:)
粒子群优化算法(PSO:Particle swarm optimization) 是一种进化计算技术。源于对鸟群捕食的行为研究。它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。
PSO的优势:在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。
1.2 直观理解
场景:一群鸟在搜索实物,假设:
- 所有的鸟都不知道食物在哪
- 它们知道自己的位置距离食物有多远
- 它们知道离实物最近的鸟的位置
然后鸟会怎么做?
每一只鸟会根据“自己的位置”和“群体最近的位置”移动到一个新的位置,不断重复这个过程,直到找到食物。
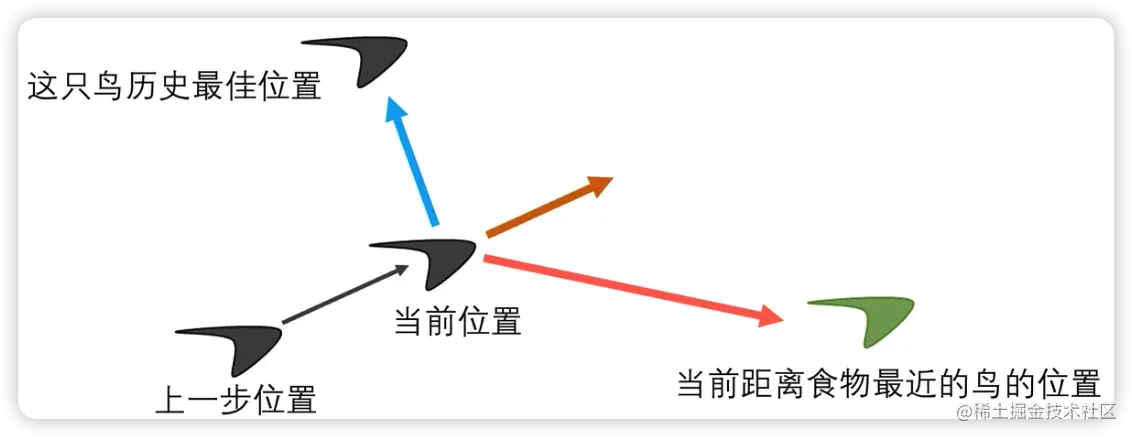
主要有三部分组成:
- 这只鸟的历史最佳位置
- 离食物最近的鸟的位置
- 上一步的惯性
所涉及到参数:
- c1:个体学习因子,也称为个体加速因子
- c2:社会学习因子,也称为社会加速因子
- r1、r2:随机数0~1
- w:惯性权重,也称为惯性系数
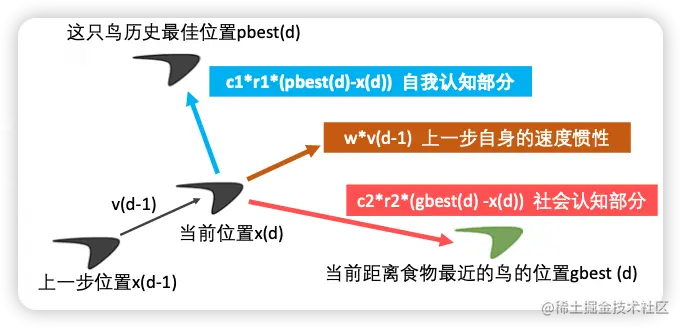
这只鸟d步所在的位置 = 上一步的位置 + 上一步的速度*运动时间
x d = x d − 1 + v d − 1 ∗ t x_d = x_{d-1} + v_{d-1}*t xd=xd−1+vd−1∗t
这只鸟d步的速度 = 上一步的速度惯性 + 自我认知部分 + 社会认知部分
v d = w ∗ v d − 1 + c 1 ∗ r 1 ∗ ( p h e s t d − x d ) + c 2 ∗ r 2 ∗ ( g b e s t d − x d ) v_d = w*v_{d-1} + c_1*r_1 * (phest_d -x_d) + c_2*r_2*(gbest_d - x_d) vd=w∗vd−1+c1∗r1∗(phestd−xd)+c2∗r2∗(gbestd−xd)
1.3 概念
- 粒子:优化问题的候选解
- 位置:候选解所在的位置
- 速度:候选解移动的速度
- 适应度:评价粒子的优劣,一般设置为目标函数值
- 个体最佳位置:单个粒子迄今为止找到的最佳位置
- 群体最佳位置:所有粒子迄今为止找到的最佳位置
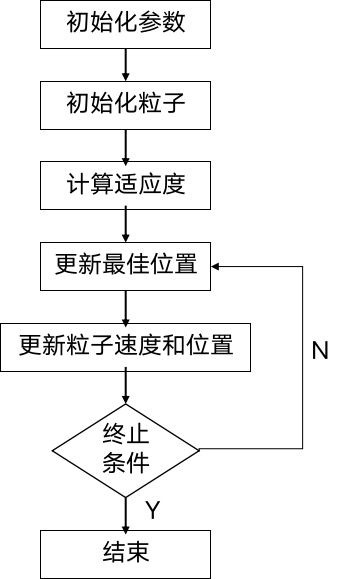
2. 算法流程
- 初始化: 随机生成一群粒子的初始位置和速度,并初始化最佳个体位置和最佳群体位置。
- **评估: ** 计算每个粒子的适应度,即目标函数值。
- 更新最佳位置: 将每个粒子的当前位置与其历史最佳位置进行比较,并更新个体最佳位置和群体最佳位置。
- 更新速度和位置: 根据个体最佳位置和群体最佳位置,以及一些权重和随机因素,更新粒子的速度和位置。
- 终止条件判断: 检查是否满足停止条件,例如达到最大迭代次数或目标函数值满足要求。
- 迭代: 如果终止条件未满足,则重复步骤3至5,直到满足终止条件。
2.1 公式
2.1.1 符号说明
- n: 粒子个数
- c 1 c_1 c1 : 个体学习因子
- c 2 c_2 c2 : 社会学习因子
- w: 速度惯性权重
- v i d v_i^d vid : 第i个粒子的第d次迭代时的速度
- x i d x_i^d xid : 第i个粒子的第d次迭代时的位置
- f ( x ) f(x) f(x) : 在x位置的实用度
- p b e s t i d pbest_i^d pbestid : 第i个粒子迭代到d次为止的最好位置
- g b e s t i d gbest_i^d gbestid : 所有粒子迭代到d次为止最好的位置
2.1.2 速度公式
这只鸟第d步的速度 = 上一步自身的速度惯性 + 自我认知部分 + 社会认知部分
v i d = w ∗ v i d − 1 + c 1 ∗ r 1 ∗ ( p b e s t i d − x i d ) + c 2 ∗ r 2 ∗ ( g b s e t i d − x i d ) v_i^d = w*v_i^{d-1} + c_1*r_1*(pbest_i^d - x_i^d) + c_2*r_2 * (gbset_i^d - x_i^d) vid=w∗vid−1+c1∗r1∗(pbestid−xid)+c2∗r2∗(gbsetid−xid)
说明:
- 学习因子一般取2
- 惯性权重一般取0.9~1.2
2.1.3 位置公式
这只鸟第d步所在的位置 = 第d-1步所在位置 + 第d-1步的速度*运动时间t(每一步的运动时间一般取1)
x i d + 1 = x i d + v i d x_i^{d+1} = x_i^d + v_i^d xid+1=xid+vid
3. 案例
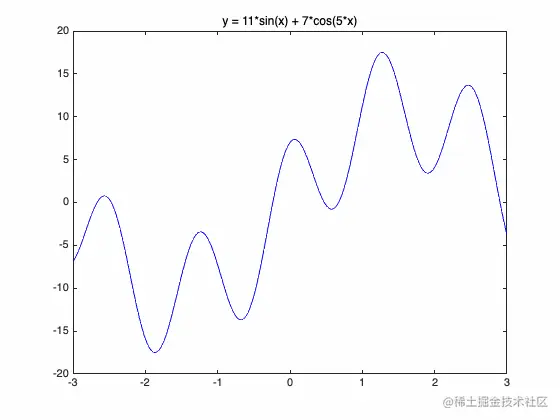
3.1 案例一:一元函数最大值
求函数 y = 11 s i n ( x ) + 7 c o s ( 5 x ) y = 11sin(x) + 7cos(5x) y=11sin(x)+7cos(5x) 在[-3,3]内的最大值,
matlab代码如下:
%% 粒子群算法PSO: 求解函数y = 11*sin(x) + 7*cos(5*x)在[-3,3]内的最大值(动画演示)
clear; clc
%% 绘制函数的图形
x = -3:0.01:3;
y = 11*sin(x) + 7*cos(5*x);
figure(1)
plot(x,y,'b-')
title('y = 11*sin(x) + 7*cos(5*x)')
hold on % 不关闭图形,继续在上面画图
%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)
n = 10; % 粒子数量
narvs = 1; % 变量个数
c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数
c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数
w = 0.9; % 惯性权重
K = 50; % 迭代的次数
vmax = 1.2; % 粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界
%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])
% 注意:这种写法只支持2017及之后的Matlab,老版本的同学请自己使用repmat函数将向量扩充为矩阵后再运算。
% 即:v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);
% 注意:x的初始化也可以用一行写出来: x = x_lb + (x_ub-x_lb).*rand(n,narvs) ,原理和v的计算一样
% 老版本同学可以用x = repmat(x_lb, n, 1) + repmat((x_ub-x_lb), n, 1).*rand(n,narvs)
%% 计算适应度
fit = zeros(n,1); % 初始化这n个粒子的适应度全为0
for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度
fit(i) = Obj_fun1(x(i,:)); % 调用Obj_fun1函数来计算适应度(这里写成x(i,:)主要是为了和以后遇到的多元函数互通)
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)
ind = find(fit == max(fit), 1); % 找到适应度最大的那个粒子的下标
gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)
%% 在图上标上这n个粒子的位置用于演示
h = scatter(x,fit,80,'*r'); % scatter是绘制二维散点图的函数,80是我设置的散点显示的大小(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)
%% 循环k次体:更新粒子速度和位置
fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度
for d = 1:K % 开始迭代,一共迭代K次
for i = 1:n % 依次更新第i个粒子的速度与位置
v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度
% 如果粒子的速度超过了最大速度限制,就对其进行调整
for j = 1: narvs
if v(i,j) < -vmax(j)
v(i,j) = -vmax(j);
elseif v(i,j) > vmax(j)
v(i,j) = vmax(j);
end
end
x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
% 如果粒子的位置超出了定义域,就对其进行调整
for j = 1: narvs
if x(i,j) < x_lb(j)
x(i,j) = x_lb(j);
elseif x(i,j) > x_ub(j)
x(i,j) = x_ub(j);
end
end
fit(i) = Obj_fun1(x(i,:)); % 重新计算第i个粒子的适应度
if fit(i) > Obj_fun1(pbest(i,:)) % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置
end
if fit(i) > Obj_fun1(gbest) % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置
end
end
fitnessbest(d) = Obj_fun1(gbest); % 更新第d次迭代得到的最佳的适应度
pause(0.1) % 暂停0.1s
h.XData = x; % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化)
h.YData = fit; % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化)
end
figure(2)
plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是:'); disp(gbest)
disp('此时最优值是:'); disp(Obj_fun1(gbest))
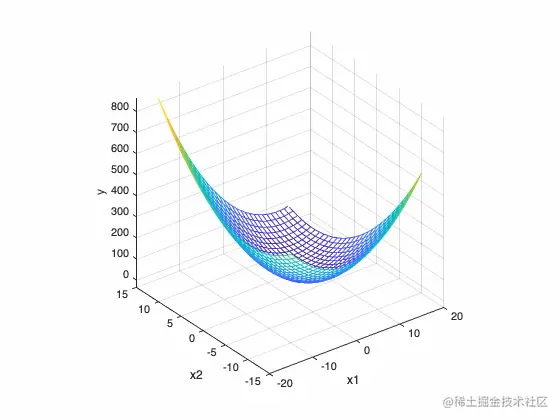
3.2 案例二:二元函数最小值
matlab代码如下:
%% 粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)
clear; clc
%% 绘制函数的图形
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on % 不关闭图形,继续在上面画图
%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)
n = 30; % 粒子数量
narvs = 2; % 变量个数
c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数
c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数
w = 0.9; % 惯性权重
K = 100; % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界
%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])
% 注意:这种写法只支持2017及之后的Matlab,老版本的同学请自己使用repmat函数将向量扩充为矩阵后再运算。
% 即:v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);
% 注意:x的初始化也可以用一行写出来: x = x_lb + (x_ub-x_lb).*rand(n,narvs) ,原理和v的计算一样
% 老版本同学可以用x = repmat(x_lb, n, 1) + repmat((x_ub-x_lb), n, 1).*rand(n,narvs)
%% 计算适应度(注意,因为是最小化问题,所以适应度越小越好)
fit = zeros(n,1); % 初始化这n个粒子的适应度全为0
for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度
fit(i) = Obj_fun2(x(i,:)); % 调用Obj_fun2函数来计算适应度
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)
ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标
gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)
%% 在图上标上这n个粒子的位置用于演示
h = scatter3(x(:,1),x(:,2),fit,'*r'); % scatter3是绘制三维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)
%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度
for d = 1:K % 开始迭代,一共迭代K次
for i = 1:n % 依次更新第i个粒子的速度与位置
v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度
% 如果粒子的速度超过了最大速度限制,就对其进行调整
for j = 1: narvs
if v(i,j) < -vmax(j)
v(i,j) = -vmax(j);
elseif v(i,j) > vmax(j)
v(i,j) = vmax(j);
end
end
x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
% 如果粒子的位置超出了定义域,就对其进行调整
for j = 1: narvs
if x(i,j) < x_lb(j)
x(i,j) = x_lb(j);
elseif x(i,j) > x_ub(j)
x(i,j) = x_ub(j);
end
end
fit(i) = Obj_fun2(x(i,:)); % 重新计算第i个粒子的适应度
if fit(i) < Obj_fun2(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度
pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置
end
if fit(i) < Obj_fun2(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度
gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置
end
end
fitnessbest(d) = Obj_fun2(gbest); % 更新第d次迭代得到的最佳的适应度
pause(0.1) % 暂停0.1s
h.XData = x(:,1); % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化)
h.YData = x(:,2); % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化)
h.ZData = fit; % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)
end
figure(2)
plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是:'); disp(gbest)
disp('此时最优值是:'); disp(Obj_fun2(gbest))
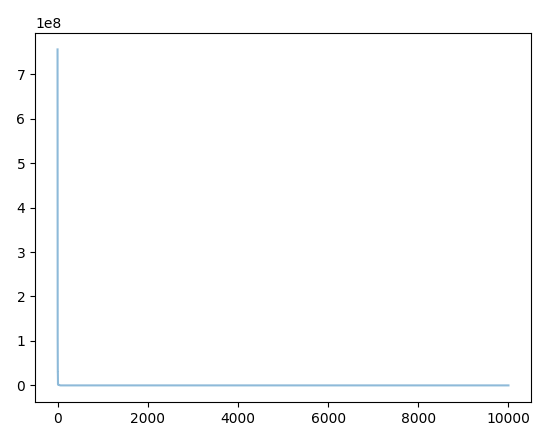
3.3 案例三:思维函数优化

python 代码如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def fit_fun(x): # 适应函数
return sum(100.0 * (x[0][1:] - x[0][:-1] ** 2.0) ** 2.0 + (1 - x[0][:-1]) ** 2.0)
class Particle:
# 初始化
def __init__(self, x_max, max_vel, dim):
self.__pos = np.random.uniform(-x_max, x_max, (1, dim)) # 粒子的位置
self.__vel = np.random.uniform(-max_vel, max_vel, (1, dim)) # 粒子的速度
self.__bestPos = np.zeros((1, dim)) # 粒子最好的位置
self.__fitnessValue = fit_fun(self.__pos) # 适应度函数值
def set_pos(self, value):
self.__pos = value
def get_pos(self):
return self.__pos
def set_best_pos(self, value):
self.__bestPos = value
def get_best_pos(self):
return self.__bestPos
def set_vel(self, value):
self.__vel = value
def get_vel(self):
return self.__vel
def set_fitness_value(self, value):
self.__fitnessValue = value
def get_fitness_value(self):
return self.__fitnessValue
class PSO:
def __init__(self, dim, size, iter_num, x_max, max_vel, tol, best_fitness_value=float('Inf'), C1=2, C2=2, W=1):
self.C1 = C1
self.C2 = C2
self.W = W
self.dim = dim # 粒子的维度
self.size = size # 粒子个数
self.iter_num = iter_num # 迭代次数
self.x_max = x_max
self.max_vel = max_vel # 粒子最大速度
self.tol = tol # 截至条件
self.best_fitness_value = best_fitness_value
self.best_position = np.zeros((1, dim)) # 种群最优位置
self.fitness_val_list = [] # 每次迭代最优适应值
# 对种群进行初始化
self.Particle_list = [Particle(self.x_max, self.max_vel, self.dim) for i in range(self.size)]
def set_bestFitnessValue(self, value):
self.best_fitness_value = value
def get_bestFitnessValue(self):
return self.best_fitness_value
def set_bestPosition(self, value):
self.best_position = value
def get_bestPosition(self):
return self.best_position
# 更新速度
def update_vel(self, part):
vel_value = self.W * part.get_vel() + self.C1 * np.random.rand() * (part.get_best_pos() - part.get_pos()) \
+ self.C2 * np.random.rand() * (self.get_bestPosition() - part.get_pos())
vel_value[vel_value > self.max_vel] = self.max_vel
vel_value[vel_value < -self.max_vel] = -self.max_vel
part.set_vel(vel_value)
# 更新位置
def update_pos(self, part):
pos_value = part.get_pos() + part.get_vel()
part.set_pos(pos_value)
value = fit_fun(part.get_pos())
if value < part.get_fitness_value():
part.set_fitness_value(value)
part.set_best_pos(pos_value)
if value < self.get_bestFitnessValue():
self.set_bestFitnessValue(value)
self.set_bestPosition(pos_value)
def update_ndim(self):
for i in range(self.iter_num):
for part in self.Particle_list:
self.update_vel(part) # 更新速度
self.update_pos(part) # 更新位置
self.fitness_val_list.append(self.get_bestFitnessValue()) # 每次迭代完把当前的最优适应度存到列表
print('第{}次最佳适应值为{}'.format(i, self.get_bestFitnessValue()))
if self.get_bestFitnessValue() < self.tol:
break
return self.fitness_val_list, self.get_bestPosition()
if __name__ == '__main__':
# test 香蕉函数
pso = PSO(4, 5, 10000, 30, 60, 1e-4, C1=2, C2=2, W=1)
fit_var_list, best_pos = pso.update_ndim()
print("最优位置:" + str(best_pos))
print("最优解:" + str(fit_var_list[-1]))
plt.plot(range(len(fit_var_list)), fit_var_list, alpha=0.5)
plt.show()
参考
[1] https://blog.csdn.net/qq_38048756/article/details/108945267
[2] https://juejin.cn/post/7159457607055310885#heading-19
[3] https://zhuanlan.zhihu.com/p/398856271