文章目录
- Arrays.sort()时间复杂度o(n)
- 二分法时间复杂度o(logn)
- 1.搜索插入位置
- 代码
- 2. 搜索二维矩阵
- 思路:
- 代码:
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 思路:
- 代码:
- 153. 寻找旋转排序数组中的最小值
- 思路:
- 代码:
- 81.搜索旋转排序数组
- 思路:
- 代码
- 4. 寻找两个正序数组的中位数[hard]
- 思路:还没看,不会做
Arrays.sort()时间复杂度o(n)
二分法时间复杂度o(logn)
1.搜索插入位置
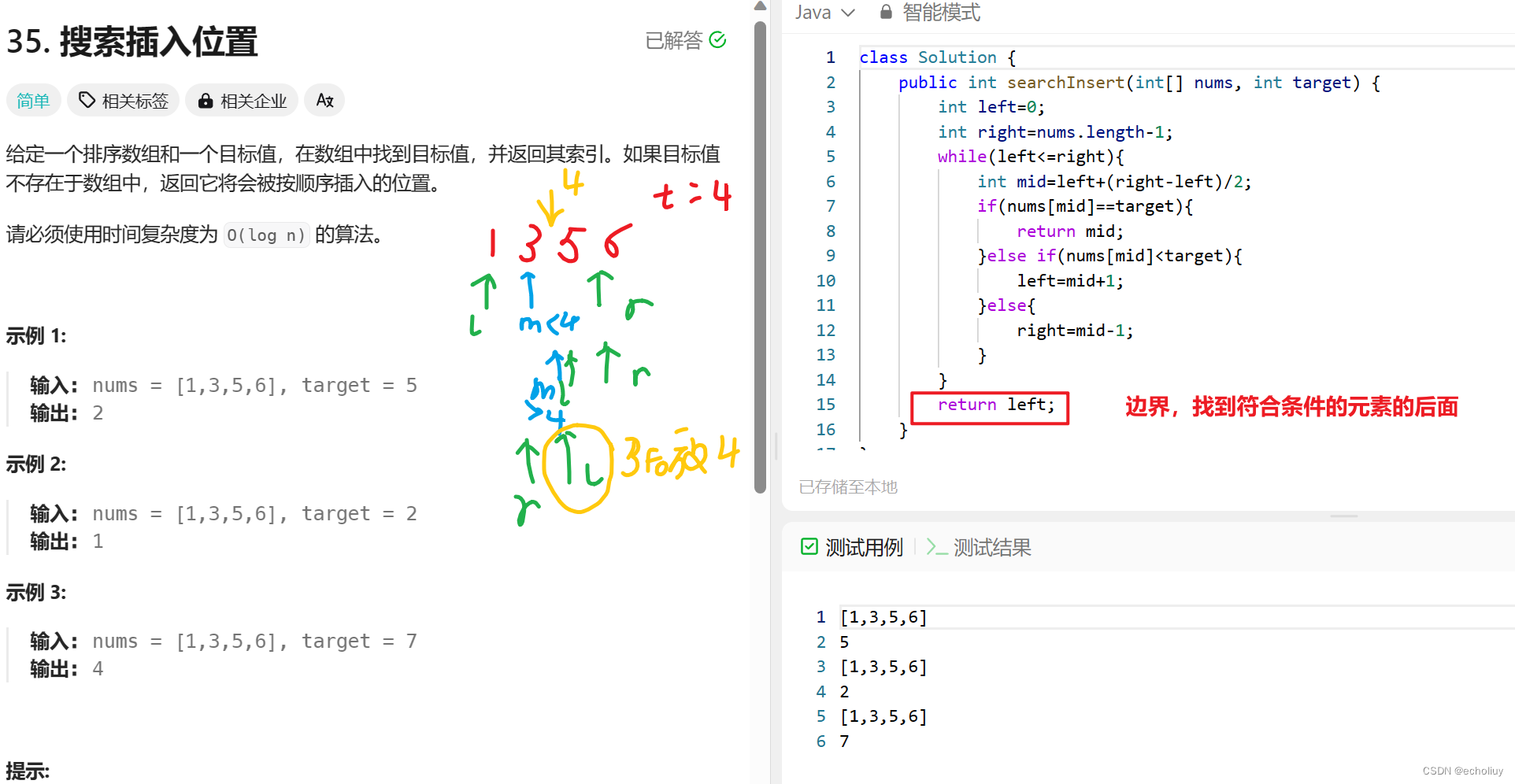
代码
class Solution {
public int searchInsert(int[] nums, int target) {
int left=0;
int right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
return mid;
}else if(nums[mid]<target){
left=mid+1;
}else{
right=mid-1;
}
}
return left;
}
}
2. 搜索二维矩阵

思路:
由于每行的第一个元素大于前一行的最后一个元素,且每行元素是升序的,所以每行的第一个元素大于前一行的第一个元素,因此矩阵第一列的元素是升序的。
我们可以对矩阵的第一列的元素二分查找,找到最后一个不大于目标值的元素,然后在该元素所在行中二分查找目标值是否存在。
先查找行,再查找列。
代码:
注意:需要判断列是否越界
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int left=0;
int right=matrix.length-1;
// 第一次二分查找,先查找行
while(left<=right){
int mid=left+(right-left)/2;
if(matrix[mid][0]==target){
return true;
}else if(matrix[mid][0]<target){
left=mid+1;
}else{
right=mid-1;
}
}
int row=right;//获取到元素所在的行
if(row<0)return false;
//当元素在第一行也没有查找到时,row是left(0)的前一个,这个时候数组index会报错,所以提前进行判断
left=0;
right=matrix[0].length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(matrix[row][mid]==target){
return true;
}else if(matrix[row][mid]<target){
left=mid+1;
}else{
right=mid-1;
}
}
return false;
}
}
34. 在排序数组中查找元素的第一个和最后一个位置

思路:
先找左边界,再找右边界。通过条件判断是否为边界,
注意:返回一个数组,则使用new int[] {1,2}的形式
代码:
class Solution {
public int[] searchRange(int[] nums, int target) {
int num1=searchLeft(nums,target);
int num2=searchRight(nums,target);
// return [num1,num2];
return new int[] {num1,num2};
}
public int searchLeft(int[] nums, int target){
int left=0;
int right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
if(mid==0||nums[mid]!=nums[mid-1]){
return mid;
}else{
right=mid-1;
}
}else if(nums[mid]<target){
left=mid+1;
}else{
right=mid-1;
}
}
return -1;
}
public int searchRight(int[] nums, int target){
int left=0;
int right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
if(mid==nums.length-1||nums[mid]!=nums[mid+1]){
return mid;
}else{
left=mid+1;
}
}else if(nums[mid]<target){
left=mid+1;
}else{
right=mid-1;
}
}
return -1;
}
}
153. 寻找旋转排序数组中的最小值

思路:
注意:在考虑选取最后一个点进行判断时,包含了顺序的情况,但是移动太诡异了,我不考虑。
而在选取第一个点进行临界值判断时,如果有顺序的情况会越界,所以先判断是不是按顺序,再跟第一个点比较。
p=nums[0],当nums[mid]数值比p大时,说明在旋转点的左边,也就是最小值的左边,所以直接将左指针转移到mid的右边,去考虑右边的区间。
当nums[mid]数值<=p时,说明在旋转点的右边,也就是最小值的右边,所以直接将左指针转移到mid的右边,去考虑右边的区间。
代码:
class Solution {
public int findMin(int[] nums) {
// Arrays.sort(nums); O(nlogn)
// return nums[0];
//二分法
int left=0,right=nums.length-1;
//如果没有旋转,第一个数就是最小的
if(nums[left]<=nums[right]){
return nums[left];
}
int p=nums[0];// 将临界点设置为数组的第一个值
while(left<=right){
// System.out.println("b-right"+right);
// System.out.println("b-left"+left);
int mid=left+(right-left)/2;
if(nums[mid]<p){
right=mid-1;
}else if(nums[mid]>=p){
left=mid+1;
}
}//旋转点是right
//则要找到的值就是旋转点的后一个,left
return nums[left];
}
}
81.搜索旋转排序数组

思路:
这道题其实是要我们明确「二分」的本质是什么。
「二分」不是单纯指从有序数组中快速找某个数,这只是「二分」的一个应用。
「二分」的本质是两段性,并非单调性。只要一段满足某个性质,另外一段不满足某个性质,就可以用「二分」。
经过旋转的数组,显然前半段满足 >= nums[0],而后半段不满足 >= nums[0]。我们可以以此作为依据,通过「二分」找到旋转点。
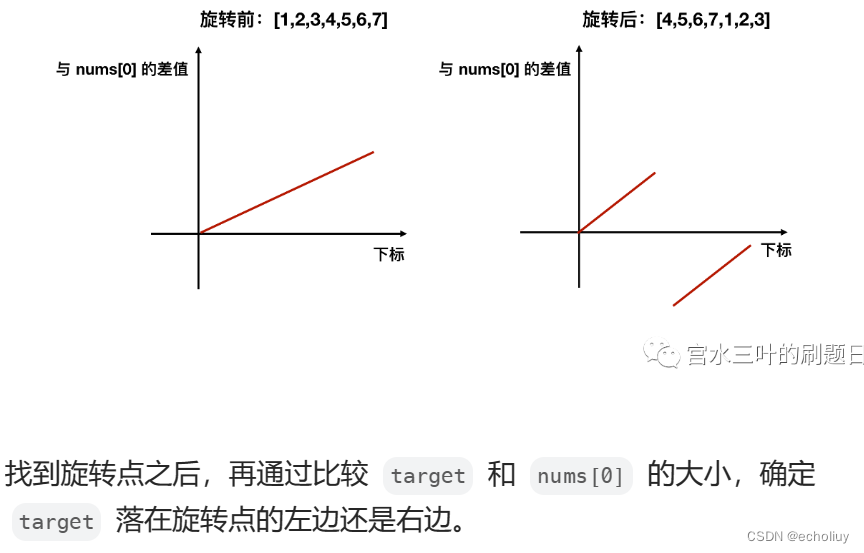
先找旋转点。再根据target和nums[0]的取值判断是在0-旋转点 还是旋转点+1到末尾之间。
代码
class Solution {
public int search(int[] nums, int target) {
//先找旋转点
int n=nums.length-1;
int left=0,right=n;
int p=nums[0];
// if(nums[left]<=nums[right])//说明是顺序数组
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]<p){
right=mid-1;
}else{
left=mid+1;
}
System.out.println(left); //左侧
}
//则旋转点就是left-1(right)
//重新计算left right值
if(target>=p){
left=0;
}else{
// l=left;
right=n;
}
//第二次二分
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]>target){
right=mid-1;
}else if(nums[mid]<target){
left=mid+1;
}else{
return mid;
}
}
return -1;
}
}
4. 寻找两个正序数组的中位数[hard]